数据结构——二叉树

二叉树的定义

二叉树是每个结点最多有两个子树的有序树。通常子树的根被称作“左子树”（left subtree）和“右子树”（right subtree）。
（1）二叉树的每个个结点最多只有两颗子树，即二叉树中结点的度只能为0、1、2.
(2)子树有左右顺序之分，不能颠倒。

根据二叉树的定义，可以知道二叉树共有五种基本的形态，如下图所示。
（1）
（2）
（3）
（4）
（5）

（1）特殊的二叉树

（1）满二叉树
在一颗二叉树中，如果所有的分支结点都有左孩子和右孩子结点，并且叶子结点都集中在二叉树的最下一层，则这样的二叉树称为满二叉树。如下图所示。

（）完全二叉树
如果对一颗深度为K、有n个结点的二叉树进行编号后，各结点的编号，与深度为k的满二叉树中相同位置上的结点编号均相同，那么这颗二叉树就是一颗完全二叉树。
下图中的完全二叉树各个结点的编号与上图满二叉树相同位置上的编号均相同，那么此时下图中的二叉树就是完全二叉树。

二叉树的主要性质

性质1：非空二叉树上叶子结点数等于双分支结点数加1.

性质2：二叉树的第 i 层上最多有 2^(i-1) 个结点（i>=1）。

性质3：高度（或深度）为 k 的二叉树中，最多有2^k-1（k>=1）个结点，换句话说，
满二叉树中前k层的结点个数为 2^k-1

性质4:具有n(n>=1)个结点的完全二叉树的深度(高度)为⌊log2(n)⌋＋1 。
性质5：对一棵具有 n 个结点的完全二叉树中的结点从 1 开始按层序编号，则对于任意的编号为i（1 < =i <= n）的结点，有：
  1.如果i>1，则结点i的双亲编号为⌊i/2⌋；否则结点i是根结点，无双亲。
  2.如果2i<=n，则结点i的左孩子的编号为2i；否则结点i无左孩子。
  3.如果2i+1<=n，则结点i的右孩子的编号为2i+1；否则结点i无右孩子。

二叉树的存储结构

（1）顺序存储结构

顺序存储结构即用一个数组来储存一颗二叉树，这周存储方式最适合于完全二叉树，用于存储一般二叉树会浪费大量的存储空间。
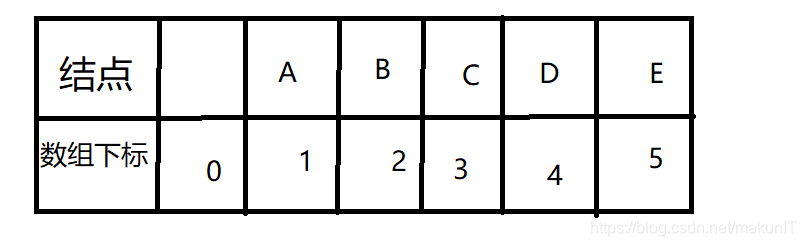
将完全二叉树中的结点值按编号依次存入一个一维数组中，即完成了一棵二叉树的顺序存储。例如将下列得完全二叉树存入数组BTree[ ] 中。

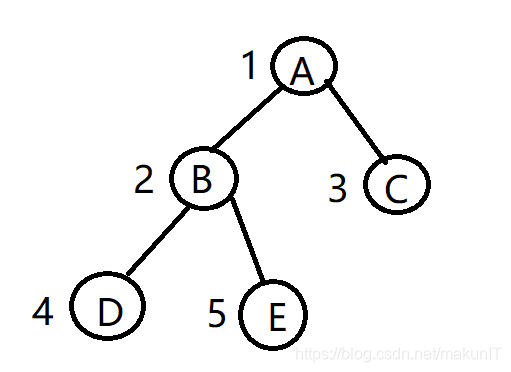
BTree[ ]

(2)链式存储结构

顺序存储结构显然有很大的局限性，不便于存储任意形态的二叉树，观察二叉树的形态可以发现是一个根结点与两棵子树之间的关系，因此设计出了还有一个数据域和两个指针域的链式结点结构，具体如下：

其中data表示数据域，用于存储对应的数据元素，lchild和rchild分别表示左指针域和右指针域，分别用于存储左孩子结点和右孩子结点的位置，这种存储结构又称为二叉链表存储结构。如下图示意图所示：

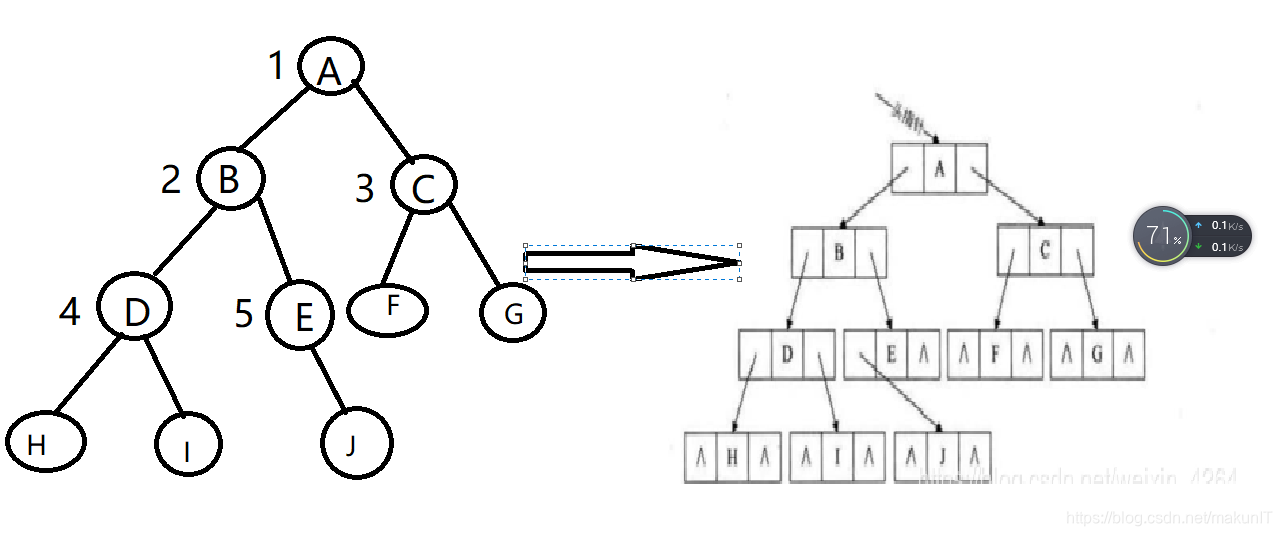
对应的结点类型的定义如下：

typedf struct BTNode
{
		char     	data;
		struct	  	BTNode  *lchild;
		struct		BTNode  *rchild;
}BTNode;

二叉树的遍历算法

先序遍历
先序遍历的操作过程如下。
如果二叉树为空树，则什么都不做；否则：
1）访问根节点
2）先序遍历左子树
3）先序遍历右子树

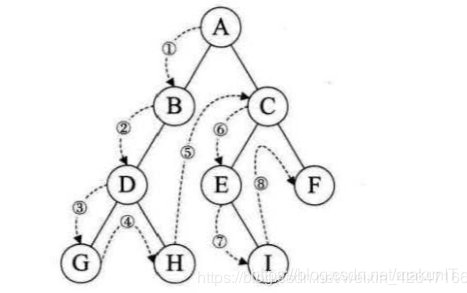
上图先序遍历的顺序为ABDHCEIF
先序遍历的算法如下：

void preorder(BTNode  *p)
{
	if(p!=NULL)
	{
		visit(p);//假设访问函数Visit（）已经定义过，其中包含了对结点p的各种访问操作，如可以打印出p对应的数值。
		preorder(p->lchild);//先序遍历左子树
		preorder(p->rchild);//先序遍历右子树
		}
}

中序遍历

中序遍历的操作过程如下。
如果二叉树为空树，则什么都不做；否则：
1）中序遍历左子树
2）访问根结点
3）中序遍历右子树

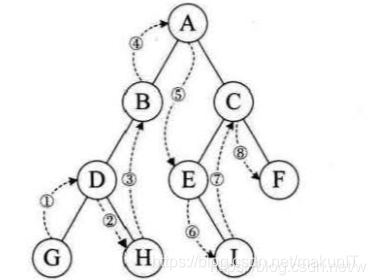
上图中序遍历为：GDHBAEICF
中序遍历的算法代码如下

void preorder(BTNode  *p)
{
	if(p!=NULL)
	{
		inorder(p->lchild)
		visit(p);
		inorder(p->rchild);
		}
}

后序遍历
后序遍历的操作过程如下。
如果二叉树为空树，则什么都不做，否则：
1）后序遍历左子树
2）后序遍历右子树
3）访问根结点

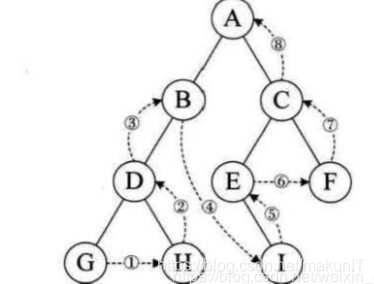
上图后序遍历的算法如下：GHDBIEFCA
后序遍历的代码如下：

void preorder(BTNode  *p)
{
	if(p!=NULL)
	{
		postorder(p->lchild);
		postorder(p->rchild);
		visit(p);
		}
}

层次遍历
规则是若树为空， 则空操作返回，否则从树的第一层，也就是根结点开始访问， 从上而下逐层遍历，在同一层中， 按从左到右的顺序对结点逐个访问。

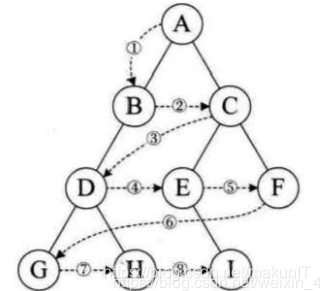
上图层次遍历的顺序为：ABCDEFGHI

综上：

二叉树遍历的性质：

已知前序遍历序列和中序遍历序列，可以唯一确定一颗二叉树。
已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。