python开发绘制构件PMM图_pmm曲线-优快云博客

本文链接：https://blog.youkuaiyun.com/m_mmnn/article/details/137235351

本文介绍了如何使用Python编程，结合《混规》标准，计算柱构件在偏心受拉、大偏心受压和小偏心受压情况下的PMM曲线，以及通过SAP2000模型的时程分析数据，实现极限承载力的绘制。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

嗨喽，大家好呀，欢迎大家一起探讨交流~~

本文主要采用python编程，根据柱构件的偏心受拉、大偏心受压、小偏心受压计算规范，实现柱类构件的PMM曲线绘制。再通过SAP 2000模型的时程分析数据导出，一键绘制。

01.构件包络曲线的算法

根据《混规》6.2.23条验算偏心受压情况下正截面受压承载力：

计算到受拉预应力筋的合力点距离： $e=e_{i}+h/2-a$

对受压钢筋取距，计算得出最大轴拉力： $N=-\frac{f_{y}\acute{A_{s}}(h_{0}-\acute{a}_{s})}{e}$

以及对应的最大弯矩值： $M_{x}=f_{y}A_{s}\acute{}(h_{0}-a_{s}\acute{})-Ne$

最后通过代码实现多选取几个点的数据，方便绘制曲线：

ea=max(20,h/30)
Asbpj=Asb+Asc/2  #b边计算钢筋
Ashpj=Ash+Asc/2  #h边计算钢筋
N=-fy*Ashpj*(b-80)/(b/2-40+ea)/1000
Mx=[]
Nx=[]
for i in range(0,20):    #对曲线取20个点数据
    nx = round(N * 0.05*(20-i),1)
    mx=round((fy*Ashpj*(b-80)-abs(nx*1000*(b/2-40+ea)))/1000000,1)
    Mx.append(mx)
    Nx.append(nx)
mx=round((fy*Ashpj*(b-80))/1000000,1)
Mx.append(mx)     #当轴力为0，弯矩最大时的点
Nx.append(0)

根据《混规》6.2.17条，计算大偏心受压：

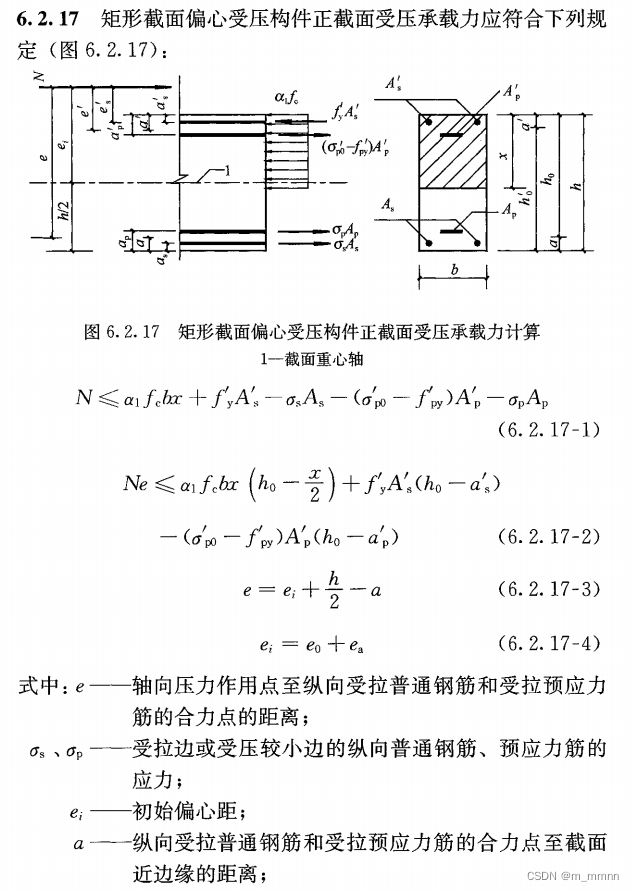
计算大偏心受压，混凝土处于界限受压区高度时，柱能够承受的最大轴力：

$N=a_{1}f_{c}bx_{b}$

根据轴力均分出20个点，求出对应点能够承受的最大弯矩：

$M=N\left ( b_{0} -\frac{N}{2a*f_{c}h}\right )$

通过代码，实现自动计算选点的数据：

for j in range(0,20):
    nx2=round(nx1*0.05*(j+1),1)
    mx2=round((nx2*((b-40)/1000-(nx2/(2*alpha(30)*fcu*h))))+(fy1*Ashpj*(b-80))/1000000-(nx2*(ea+b/2-40))/1000,1)
    Mx.append(mx2)
    Nx.append(nx2)

随后计算小偏心受压对应的最大轴力与最大弯矩：

计算轴压时能够承受的最大轴力：

$N=0.9*0.98*(f_{c}A+f_{y}^{'}A_{s}^{'})$

对最大轴力和大偏压最大轴力之间进行取点，计算对应的最大弯矩：

nx3=0.9*0.98*(fcu*(b*h-2*Ashpj)+fy1*2*Ashpj)/1000
for i in range(0,19):
    nx4=round((nx3-nx1)*0.05*(i+1)+nx1,1)
    bb=((b-40)*nx4*1000*(Xb-beta(30))-(b-40)*fy1*Ashpj*(Xb-beta(30))-fy*beta(30)*Ashpj*(b-40))/(alpha(30)*fcu*h*(b-40)*(Xb-beta(30))-fy*Ashpj)
    mx4=round(alpha(30)*fcu*1000*h/1000*bb/1000*((b-40)-bb/2)/1000+fy1*Ashpj*((b-40)-40)/1000000-nx4*(b/2-40+ea)/1000,1)
    Mx.append(mx4)
    Nx.append(nx4)

最后将得到的所有点数据放进两个列表中

02.随后进行时程分析点数据的提取

这里需要通过代码让python程序调用SAP 2000模型，这里就不介绍了，这里介绍下调用模型后导出时程分析点的代码。

SapModel.Results.Setup.SetOptionMultiStepStatic(2)   #设置非线性导出为逐步值
name=[]
Object =0
NumberResults=0
Obj = []
ObjSta = []
Elm = []
ElmSta = []
LoadCase = []
StepType = []
StepNum = []
P = []
V2 = []
V3 = []
T = []
M2 = []
M3 = []
[NumberResults, Obj, ObjSta, Elm, ElmSta, LoadCase, StepType, StepNum, P, V2, V3, T, M2, M3, ret]=SapModel.Results.FrameForce(ObjectName[0], Object, NumberResults, Obj, ObjSta, Elm, ElmSta, LoadCase, StepType, StepNum, P, V2, V3, T, M2, M3)
Npx=[-i*0.8 for i in P]
Mx_c=[i*0.8 for i in M2]
#获取y向时程分析

Npy=[-j*0.8 for j in P]
My_c=[j*0.8 for j in M3]

03.绘制构件的极限承载力

通过得到的子结构极限承载力对应的M和N点的列表，绘制成一个曲线，实现的代码如下：

设置图幅的大小，并将图分为两个小图：

plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(1,2,1)

将坐标轴和构件的极限承载力和时程分析的数据点绘制到图上：

plt.xlabel("M/KN.m", fontsize=10)
plt.ylabel("N/KN", fontsize=10)
plt.title("X向地震波", fontsize=15)
plt.scatter(Mx_c, Npx, s =5,color='r', marker='.',label='时程分析')  #绘制散点图
plt.plot(Mx, Nx,label="极限承载力")
plt.legend(['时程分析', '极限承载力'], loc='upper right')

最后设置图片的坐标轴位置，使坐标轴位于（0,0）点居中布置：

ax = plt.gca()  # 获取整张图像的坐标的对象
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
# 设置（0，0）为两坐标轴的交点
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

最后通过绘制得出的子结构极限承载力图如下图：