矩阵乘法优化

系列文章目录

神经网络优化学习笔记
卷积运算优化学习笔记

---

书籍链接: 《AI嵌入式系统：算法优化与实现》

前言

本文介绍矩阵乘法在机器学习中的应用并给出几种实际降低矩阵运算复杂度的算法，其中包括精确矩阵乘法算法和近似矩阵乘法算法。主要目的是降低数据乘法次数。

---

一.机器学习算法中的矩阵乘法

• 高维数据与降维矩阵相乘获取低纬度的特征向量。
• 神经网络的计算（全连接层 && 卷积层Im2col后转换后的矩阵相乘）。

二. Strassen矩阵相乘算法

• 基本思想：
  • 对于2*2的矩阵乘法的优化： 将8次乘法运算减少为7次乘法运算，但加法运算增加到18次。
  • 具体实现：
    $$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{cc}e& f\\ g& h\end{array}\right]=\left[\begin{array}{cc}ae+bg& af+bh\\ ce+dg& cf+dh\end{array}\right]\text{\hspace{1em}(1)}$$
    $$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{cc}e& f\\ g& h\end{array}\right]=\left[\begin{array}{cc}{p}_5+p_4-p_2+p_6& p_1+p_2\\ p_3+p_4& p_1+p_5-p_3-p_7\end{array}\right]\text{\hspace{1em}(2)}$$
    $$\{\begin{array}{rl}{p}_1& =a(f-h)\\ p_2& =(a+b)h\\ p_3& =(c+d)e\\ p_4& =d(g-e)\\ p_5& =(a+d)(e+h)\\ p_6& =(b-d)(g+h)\\ p_7& =(a-c)(e+f)\end{array}\text{\hspace{1em}(3)}$$
• 实际应用：
  • 放在矩阵乘法中，分块进行相应操作。

三. Winograd矩阵相乘算法

• 基本思想
  • 优化思路：
    $$c=a_1{b}_1+a_2{b}_2\text{\hspace{1em}(4)}$$
    $$c=m_3-m_1-m_2\text{\hspace{1em}(5)}$$
    $$\{\begin{array}{rl}{m}_1& =a_1{a}_2\\ m_2& =b_1{b}_2\\ m_3& =(a_1+b_2)(a_2+b_1)\end{array}\text{\hspace{1em}(6)}$$
  • 应用到矩阵乘法上，将第一个矩阵的列数折半，…
• 优化效果： 可以减小一半的乘法运算。

四. 低秩矩阵乘法

• 基本思想：

  • 对于秩为R，尺寸为 N X L的矩阵A，可以表示为 R个向量乘积表示：
    $$A=\sum _{r=1}^R{u}_r{v}_r^T\text{\hspace{1em}(1)}$$
    
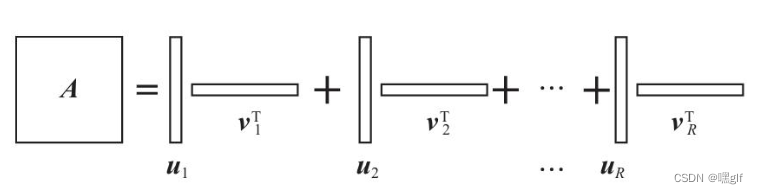
  • 此时计算矩阵A与 L X 1的列向量 x 的乘积时，利用上面的分解式：
    $$Ax=\sum _{r=1}^R{u}_r(v_r^{T}x)\text{\hspace{1em}(2)}$$
  • 此时计算复杂度从N X L 降到 （L + N）X R 。

• 获取表达式1的分解形式的方法： SVD分解。
  

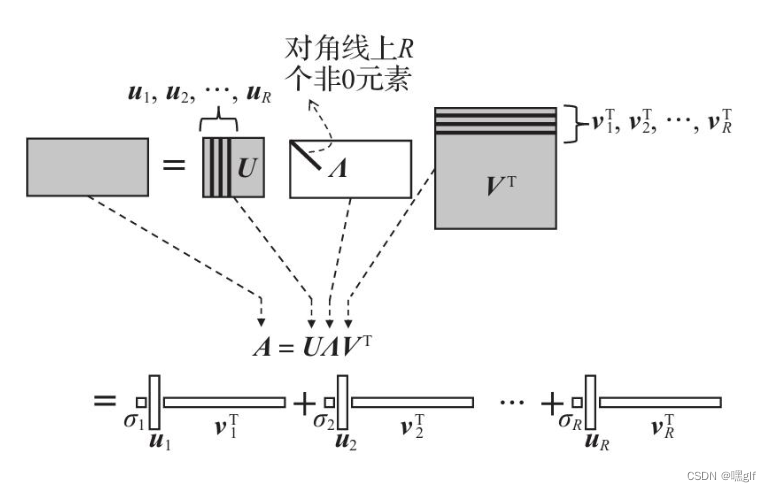
• 一般应用场景：矩阵 A一般是固定的常数矩阵

五. 循环矩阵乘法

• 转换为傅里叶变换实现

六. 近似矩阵乘法

• 基于矩阵低秩近似的矩阵乘法
  
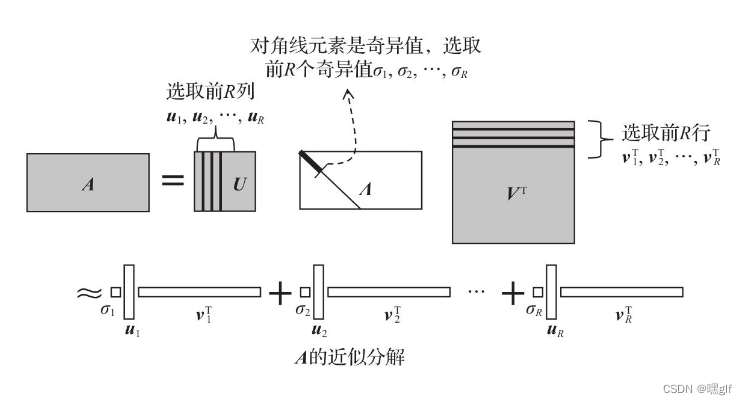
  放弃的${\sigma }_{R+1}$越小，说明后续特征的影响越小，近似结果越接近准确值；

• 基于数据统计相关性的近似矩阵乘法
  

• 基于向量量化的近似矩阵乘法

总结