参考代码:MCDP
介绍
这篇文章对于多视图自监督深度估计在不同相机下的深度表达构建一致性约束,其建立约束的信息来自于相邻相机之间的视角重叠区域,如下图所示

依据这些区域可以在loss端通过不同相机之间标定外参构建不同视角之间的深度约束关系,也就是周围相机预测出的深度经过投影之后应该和目的相机的深度值差异最小化。
除了在loss层面上对不同视角下深度构建约束之外,还在特征表达的维度在channel层次上对初次深度估计结果进行加权,使得深度表达具备更强表达能力,也使得可以通过迭代优化加权系数的方式级连优化深度估计结果。
不过在文章的消融实验中并没有去对比特征维度和loss维度这俩分别对深度一致性的贡献大小,在经典自监督深度估计中也会采用多尺度估计,要是再加上loss维度的约束,也可以看作是一种级连优化。
方法设计
深度加权因子的迭代更新
这里将网络最后生成结果描述为初次深度估计结果与加权系数叠加的形式,然后在不同的迭代轮次中不断去优化这个加权系数,而这个初次深度估计结果不变化。也就是对应下图中的迭代

那么为了使得深度加权的权重跟随相邻视角信息而发生变化,那么就需要将这俩的信息进行融合,这部分是通过集合位置warp的形式对齐到目的特征图上,也就是文中说的相机1和相机2的warp操作。对齐之后的特征cat起来去更新加权系数,它的结构也就是下图中的样子:
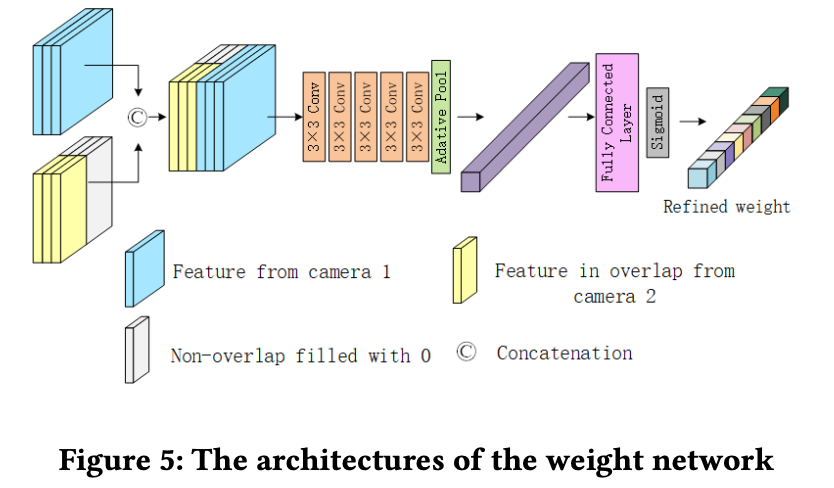
深度一致性约束loss
在下图中可以看到左右视图和中间视图它们之间是存在交叠区域的,那么可以通过warp的方式将左右视图的深度估计结果对齐到中间视图,也就是下图中的样子

上面的步骤是深度对齐,对齐之后的深度结果应该和中间视图自身估计出来的深度一致,那么就可以使用L1损失函数去约束使得它们的差异最小化。
下图展示了使用文章的方法在不同视角下深度估计的结果,可以看到添加这个约束之后不同视角下深度差异较大的情况有所缓解
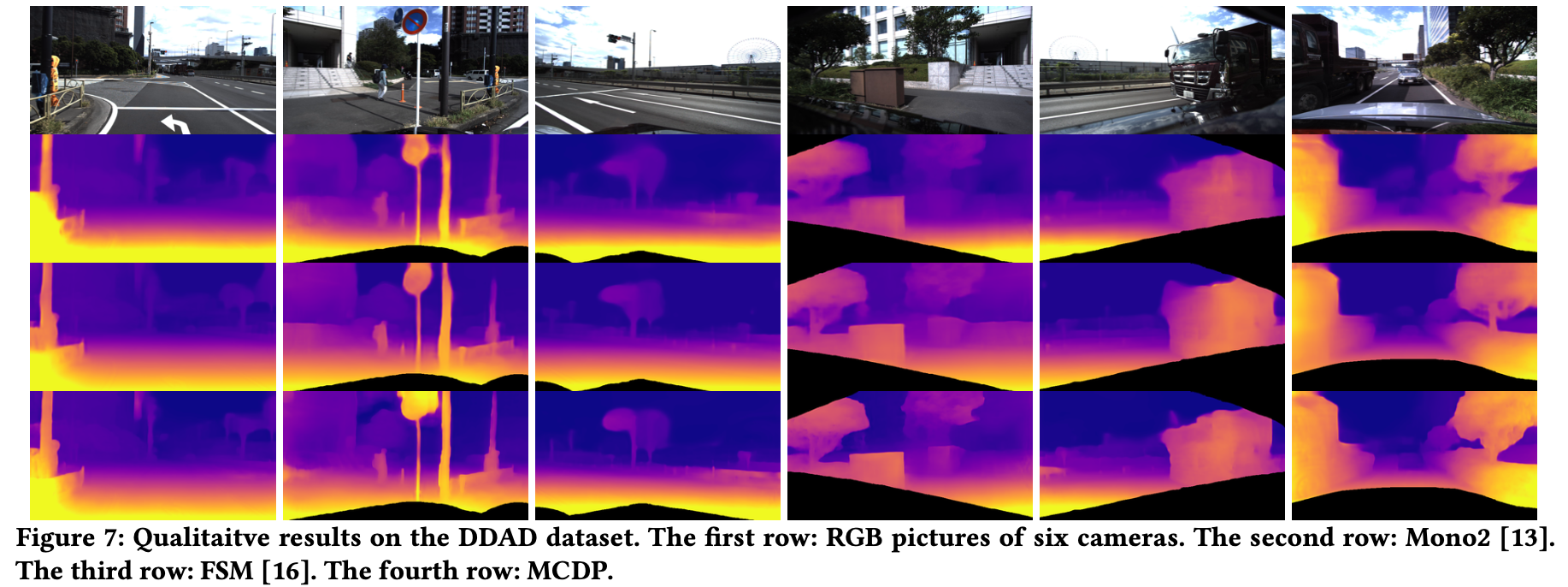
3. 实验结果
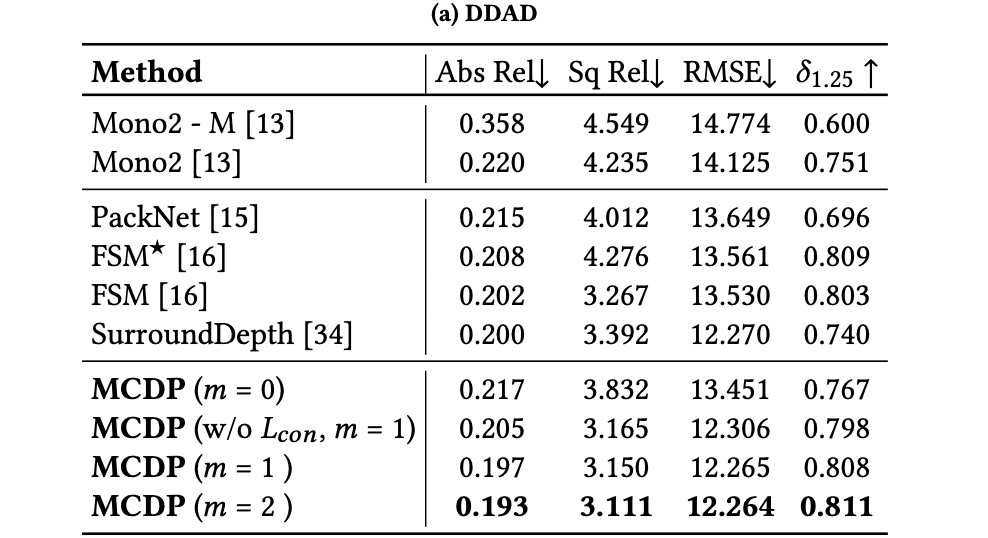























 1136
1136

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








