Frequency-Aware Self-Supervised Monocular Depth Estimation——论文笔记

参考代码：freq-aware-depth

1. 概述

介绍：在自监督深度估计算法中采用光度重构误差作为约束函数，但是这个约束函数却是存在不足的，也就是损失的大小在某些区域不能真实反应深度预测的误差大小，如图像中的高频区域，从而给整体算法Loss带来歧义（深度估计误差于光度重构误差的比例不正相关）。对于这个问题文章提出了两种策略去缓解高频区域处不确定性带来的歧义：1）Ambiguity-Masking：通过感知图像中的高频信息分布（图像梯度变化），给光度重构误差增加一个权重因子，从而缓解高频信息处Loss的不确定性。2）Auto-Blur：在图像梯度的指引下设计一个低通的高斯滤波器，用于平滑图像中的边缘区域，使得损失更能真实反馈重构的质量。

在自监督深度估计中，对图像中物体的边缘细节放大，并与对应的Loss分布可视化得到下图：

在上图（b）中可以看到loss倾向于在边缘区域产生更大的损失，这也表达了边缘处的损失并不能很好反应实际深度预测的质量。将图像中目标对应边缘进行放大得到图（c），可以看到由于分辨率的问题，其在边缘位置处的一些像素并不是能很准确进行区域划分，这也就导致了对应高频区域上loss存在歧义。这篇文章也对此提出了两点对应的策略用于缓解该问题。

2. 方法设计

2.1 整体pipeline

文章的整体pipeline见下图所示：

从上图可以看出文章在原本自监督深度估计方法的基础上，增加Ambiguity-Masking用于缓解高频区域loss歧义带来的影响，增加Auto-Blur缓解图像高频区域带来的损失跳变和歧义。

这里令网络$t$时刻估计出的深度为$D_t$，到时刻$t+n$的位姿关系为$T_{t\to t+n}$，对应的相机内参为$K$，则图像的冲投影采样描述为：
$$\otimes =proj(D_t,T_{t\to t+n},K)$$
对于图像在X和Y方向上梯度描述为：
$${\nabla }_{u\pm }(i,j)=I(i,j)-I(i\pm 1,j)$$
$${\nabla }_{v\pm }(i,j)=I(i,j)-I(i,j\pm 1)$$
在Auto_Blur中使用两个方向的梯度：
$${\nabla }_{\pm }(i,j)=||{\nabla }_{u\pm }(i,j),{\nabla }_{v\pm }(i,j)|{|}_2$$
在Ambiguity-Masking中使用合成梯度：
$$\nabla (i,j)=||\frac{{\nabla }_{u+}(i,j)-{\nabla }_{u-}(i,j)}{2},\frac{{\nabla }_{v+}(i,j)-{\nabla }_{v-}(i,j)}{2}|{|}_2$$

2.2 Ambiguity-Masking

记使用的梯度为${\mathcal{F}}_t$，使用二值掩膜$u$表示在水平和垂直方向上梯度相反的高频区域：
$$u=[{\nabla }_{u+}\cdot {\nabla }_{u-}<0\vee {\nabla }_{v+}\cdot {\nabla }_{v-}<0],[\cdot ]isIversonbracket$$
之后得到在时刻$t$下的不确定性图：
$${\mathcal{A}}_t=u\odot {\mathcal{F}}_t$$
对于在时刻$t+n$重构得到的图像其不确性图经过采样之后描述为：
$${\bar{\mathcal{A}}}_{t+n}=⟨{\mathcal{A}}_{t+n},{\otimes }_{t+n}⟩$$
最后将上述两者取最大值得到最后的不确定性图：
$${\mathcal{A}}_t^{max}=max({\bar{\mathcal{A}}}_{t+n},{\mathcal{A}}_t)$$
之后得到于光度重构误差加权的权重二值mask：
$${\mathcal{A}}_t^{pe}=[{\mathcal{A}}_t^{max}<\delta ]$$
其中，$\delta =0.3$。同时可以使用下面指数的形式计算权重：
$${\mathcal{A}}_t^{pe}=e^{-\gamma {\mathcal{A}}_t^{max}},\gamma =3$$

2.3 Auto_Blur

记使用的梯度也为${\mathcal{F}}_t$，则定义高频掩膜（阈值$\lambda =0.2$）：
$${\mathcal{M}}_{is-hf-pixel}(p)=[{\mathcal{F}}_t(p)>\lambda ]$$
依据上述高频掩膜定义，在大小为$s=9$的区域上确定高频区域（阈值为$\eta =60$）：
$${\mathcal{M}}_{is-hf-pixel}^{avg}(p)=\frac{1}{s\ast s}\sum _{q\in N_{s\ast s}(p)}{\mathcal{M}}_{is-hf-pixel}(q)$$
$${\mathcal{M}}_{is-hf-area}(p)=[{\mathcal{M}}_{is-hf-pixel}^{avg}(p)>\eta \%]$$
对于一张图像的高斯模糊，其数学表达定义为：
$$I_t^{gb}=\sum _{q\in N(p)}{w}^{gb}(q)I_t(q)$$
$$w^{gb}(q)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{\Delta }_x^2+{\Delta }_y^2}{2{\sigma }^2}}$$
则添加图像高频信息因子，得到新的滤波函数：
$$I_t^{ab}(p)=w_{blur}(p)I_t^{gb}(p)+(1-w_{blur}(p))I_t(p)$$
其中的加权因子为：
$$w_{blur}(p)={\mathcal{M}}_{is-hf-pixel}^{avg}(p){\mathcal{M}}_{is-hf-area}(p)$$
添加Auto-Blur之后深度误差曲线趋于于全监督曲线接近，达到对高频噪声的抑制作用，见下图所示：

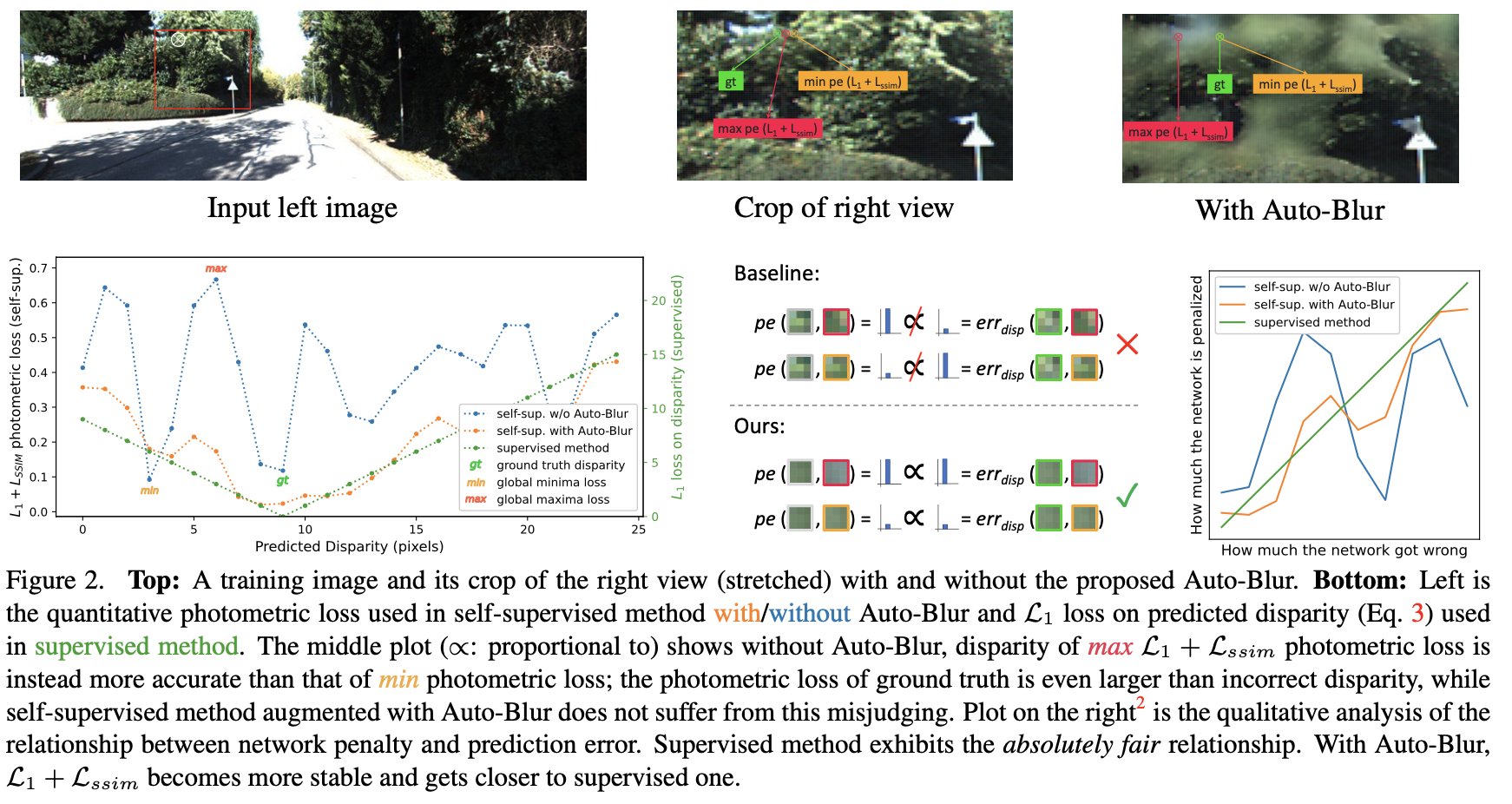
2.4 消融实验

上述两种高频信息处理策略对性能带来的影响：

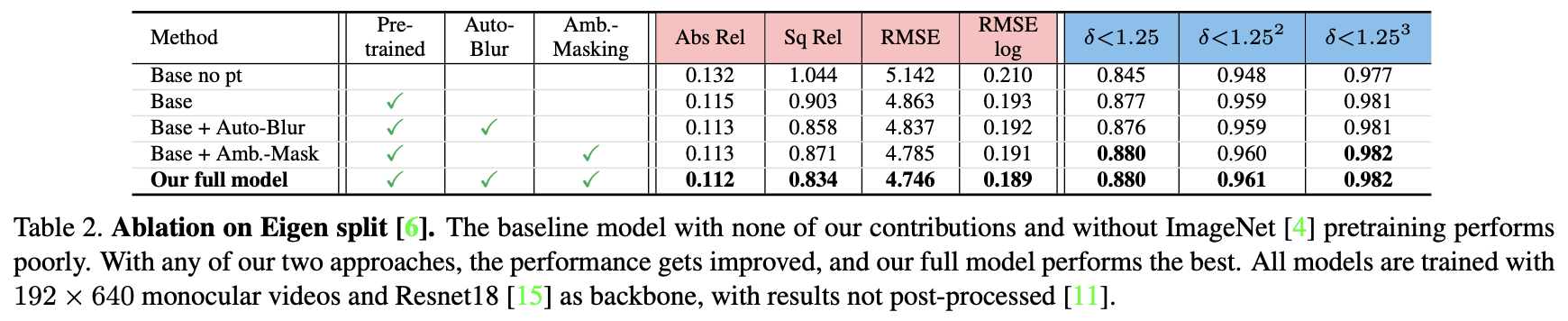
其它一些超参数带来的影响：

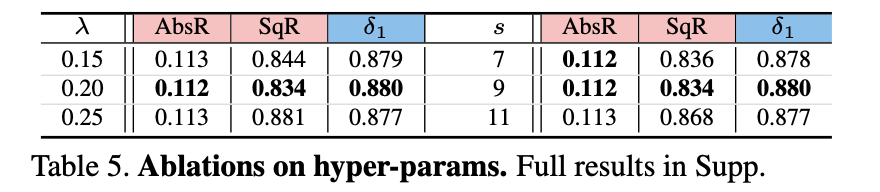
3. 实验结果

在现有方法上带来的性能提升：

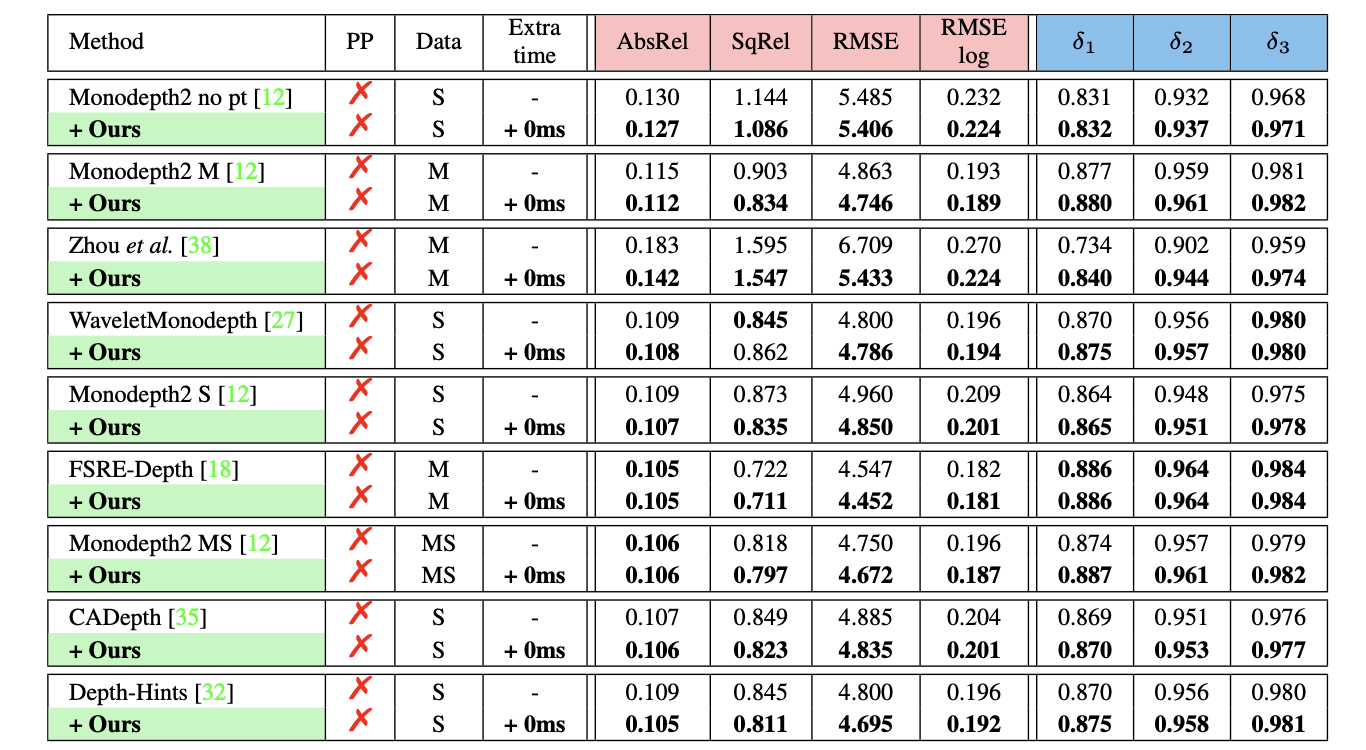
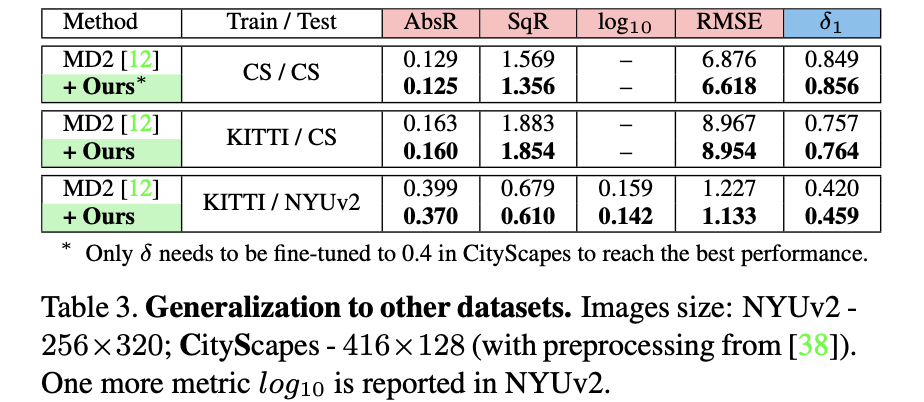
不同数据集下均表明文章方法的有效性：