差分数组算法

 1.相关定义

           差分数组本质上来说就是一个数组，可以用O(1)的时间修改数组区间.我们设原数组nums，差分数组diff，当2<=i<=n时，diff[i]=nums[i]-nums[i-1];也就是说我们对nums数组中的相邻元素进行两两做差（用右边减去左边）

                原始数组

8

2

6

3

1

8

3

                差分数组

           

8

-6

4

-3

-2

7

-5

---

2.常见用法

       当我们需要统一更新区间[l,r]（仅+，-操作），我们只需更新diff[l]+=val,diff[r+1]-=val;

3.具体案例

        a.一维差分数组

 (原题. - 力扣（LeetCode）)

车上最初有 capacity 个空座位。车 只能 向一个方向行驶（也就是说，不允许掉头或改变方向）

给定整数 capacity 和一个数组 trips ,  trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客，接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。

当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
        int[] d = new int[1001];
        for (int[] t : trips) {
            int num = t[0], from = t[1], to = t[2];
            d[from] += num;
            d[to] -= num;
        }
        int s = 0;
        for (int v : d) {
            s += v;
            if (s > capacity) {
                return false;
            }
        }
        return true;
    }
}

        模板:

        

class DifferenceArray{
    private int[] diff;
    public  DifferenceArray(int[] nums){
        diff = new int[nums.length];
        //初始化差分数组
        diff[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            diff[i] = nums[i] - nums[i-1];
        }
    }
    public void increment(int i,int j,int val){
        diff[i] += val;
        if (j+1 < diff.length){
            diff[j+1] -= val;
        }
    }
    public int[] result(){
        int[] res = new int[diff.length];
        res[0] = diff[0];
        for (int i = 1; i < diff.length; i++) {
            res[i] = res[i-1] + diff[i];
        }
        return res;
    }
}

b.二维差分数组

               

        

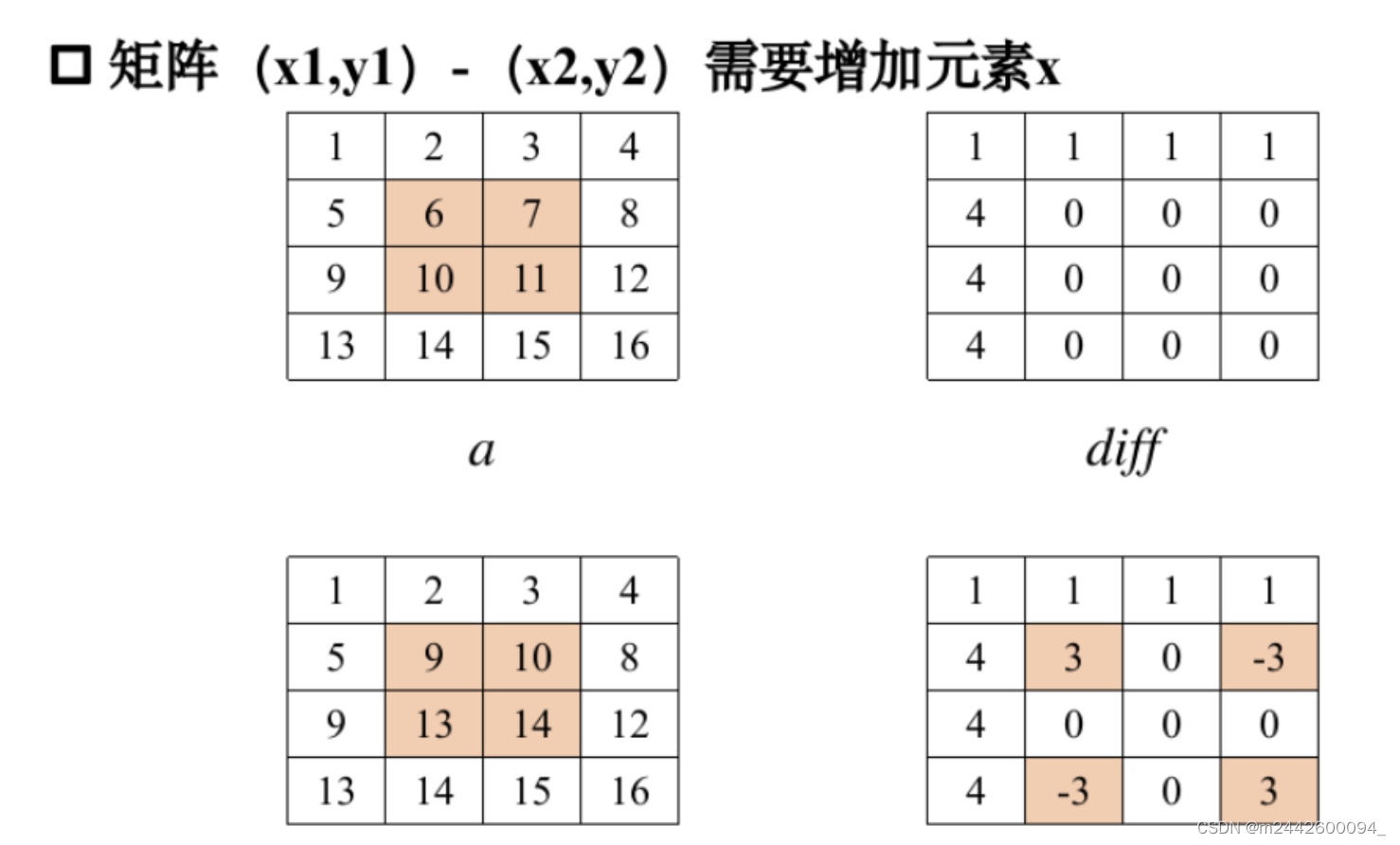
class DifferenceArrayTwo{
    private int[][] diff;
    int n,m;
    public  DifferenceArrayTwo(int[][] nums){
        n = nums.length;
        m =  nums[0].length;
        diff = new int[n][m];
        //初始化差分数组
        diff[0][0] = nums[0][0];
        for(int i = 0 ; i < n ; i ++){
            for(int j = 0 ; j < m ; j++){
                //重复元素
                int addVal = i > 0 && j >0 ? nums[i-1][j-1] : 0;
                //上侧元素
                int upperVal = i > 0 ? nums[i-1][j] : 0;
                //左侧元素
                int  leftVal = j > 0 ? nums[i][j-1] : 0;
                diff[i][j] = nums[i][j] + addVal - upperVal - leftVal;
            }
        }
    }
    //从下标0开始
    public void increment(int x1,int y1,int x2,int y2,int val){
        diff[x1-1][y1-1] += val;
        if (x2 < n){
            diff[x2][y1-1] -= val;
        }
        if (y2 < m){
            diff[x1-1][y2] -= val;
        }
        if (x2 < n && y2 < m){
            diff[x2][y2] += val;
        }
    }

    /**
     * 还原结果
     * @return
     */
    public int[][] result(){
        int[][] res = new int[n][m];
        for(int i = 0 ; i < n ; i ++){
            for (int j = 0 ; j < m ; j++){
                //重复元素
                int addVal = i > 0 && j >0 ? res[i-1][j-1] : 0;
                //上侧元素
                int upperVal = i > 0 ? res[i-1][j] : 0;
                //左侧元素
                int  leftVal = j > 0 ? res[i][j-1] : 0;
                res[i][j] = diff[i][j] - addVal + upperVal + leftVal;
            }
        }
        return res;
    }
}