杭电 1022火车进站

Problem Description

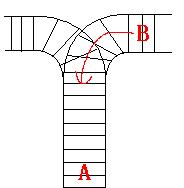
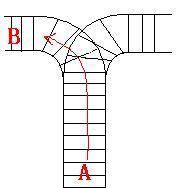
As the new term comes, the Ignatius Train Station is very busy nowadays. A lot of student want to get back to school by train(because the trains in the Ignatius Train Station is the fastest all over the world ^v^). But here comes a problem, there is only one railway where all the trains stop. So all the trains come in from one side and get out from the other side. For this problem, if train A gets into the railway first, and then train B gets into the railway before train A leaves, train A can't leave until train B leaves. The pictures below figure out the problem. Now the problem for you is, there are at most 9 trains in the station, all the trains has an ID(numbered from 1 to n), the trains get into the railway in an order O1, your task is to determine whether the trains can get out in an order O2.

 

Input

The input contains several test cases. Each test case consists of an integer, the number of trains, and two strings, the order of the trains come in:O1, and the order of the trains leave:O2. The input is terminated by the end of file. More details in the Sample Input.

 

Output

The output contains a string "No." if you can't exchange O2 to O1, or you should output a line contains "Yes.", and then output your way in exchanging the order(you should output "in" for a train getting into the railway, and "out" for a train getting out of the railway). Print a line contains "FINISH" after each test case. More details in the Sample Output.

 

Sample Input

3 123 321
3 123 312

 

Sample Output

Yes.
in
in
in
out
out
out
FINISH
No.
FINISH
 
 
 
 
 
 

可以用栈来解决这个问题  也可以用数组模拟栈来解决；
 
 
模拟栈（个人认为较栈简单）：
#include<stdio.h>
#include<string.h>
int main()
{
	int n,i,j,k,top;
	char a[200],b[200],c[200],s[200][20];
	while(~scanf("%d%s%s",&n,&a,&b))
	{
		top=i=j=k=0;
		strcpy(s[k++],"in");//字符串复制并保存 
		while(i<n)
		{
			c[top]=a[i];
			while(c[top]==b[j]&&b[j]!='\0'&&c[top]!='\0')//比较是否相同 
			{
				top--;
				j++;
				strcpy(s[k++],"out");
			}
			i++;
			top++;
			strcpy(s[k++],"in");
		}
		if(top==0)
		{
			printf("Yes.\n");
			for(i=0;i<k-1;i++)
			puts(s[i]);
			printf("FINISH\n");
		}
		else
		printf("No.\nFINISH\n");
	}
	return 0;
}
 
 
栈：
 
 
/*后进先出（Last In First Out），简称为LIFO线性表。
栈的基本运算有六种：

构造空栈：Stack<>.s

判栈空: s.Empty()

判栈满： s.Full(S)、

进栈： s.Push(x)  可形象地理解为压入，这时栈中会多一个元素

退栈： s.Pop()   可形象地理解为弹出，弹出后栈中就无此元素了。

取栈顶元素：S.Top() 不同与弹出，只是使用栈顶元素的值，该元素仍在栈顶不会改变。*/
#include<iostream>
#include<stdio.h>
#include<stack>
#include<algorithm>
using namespace std;
int main()
{
	stack<char>s;
	char a[1001],b[1001];
	int n,i,j,count,c[1001];
	while(~scanf("%d",&n))
	{
		count=0;
		j=0;
		getchar();
		while(!s.empty())//**清空栈**//
		{
			s.pop();
		}
		scanf("%s %s",a,b);
		for(i=0;i<n;i++)
		{
			s.push(a[i]);//**入栈**//
			c[count]=1;//**进行标记**//
			count++;
		    while(j<n&&!s.empty())//**i进行移动而且栈为非空**//
			{
				if(s.top()==b[j])//**栈首相同**//
				{
					s.pop();//**出栈**//
				    c[count]=0;//**标记出栈**//
				    count++;
				    j++;//**j往右移动**//
				}
			    else
				{
				    break;
				}
			}
		}
		if(s.empty())
		{
			printf("Yes.\n");
			for(i=0;i<count;i++)
			{
				if(c[i]==1) printf("in\n");
				else if(c[i]==0)
					printf("out\n");
			}
		}
		else
		{
			printf("No.\n");
		}
		printf("FINISH\n");
	}
	return 0;
}