【图】（三）顶点度的计算 - C语言

原创已于 2022-12-05 14:55:34 修改 · 5.9k 阅读

33 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #图论

于 2022-11-01 08:00:00 首次发布

数据结构专栏收录该内容

12 篇文章

订阅专栏

顶点度的计算

1 邻接矩阵计算顶点的度

2 邻接表计算顶点的度

顶点度的计算

对于无向图来说，顶点的度 $deg(v_i)$ 就等于与其相邻接的顶点的个数；而对于有向图来说，由于边的方向性，顶点的度很自然地被分为了入度 $id(v_i)$ 和出度 $od(v_i)$ 。有向图出度与入度的计算与无向图顶点的度的计算大同小异，因此仅以无向图为例。

1 邻接矩阵计算顶点的度

首先介绍一下邻接矩阵的特点：

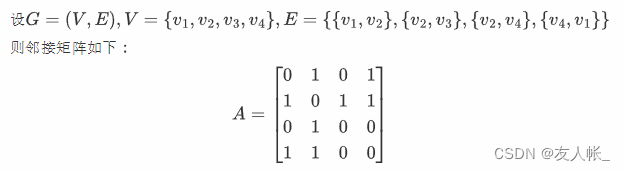
邻接矩阵中包含了以下信息：

① G的顶点数p就是G的邻接矩阵A的阶数。

② G的边数q就是A中1的个数的一半。

③ 顶点 $v_i$ 的度 $deg(v_i)$ 等于A的第i行上1的个数。

④ 若A的第i行上的全部元素都为0，则 $v_i$ 为孤立点。

⑤ A是对称且对角线上全部元素为0 (反自反且对称)。

⑥ 若两个图的邻接矩阵相等或通过交换某些行和列后相同，则这两个图是同构的。

其中，我们可以通过这一条来进行计算：

顶点 $v_i$ 的度 $deg(v_i)$ 等于A的第i行上1的个数。

显然，只需要统计矩阵某一行上非-1元的个数，便是该顶点的度。程序比较容易，请读者自行实现。

2 邻接表计算顶点的度

由邻接表的定义可以知道：

使用指针数组G[N]，G[i]代表以第i个顶点为头结点的链表，只存与之邻接的顶点。

G[i]链表的长度（除去头结点-自身）即为顶点的度。程序比较容易，代码如下：

 /* 计算邻接表个顶点的度 */
 void CalcDegree_L(AdjList L, int arr[][MaxVertexNum])
 {
     int i, count;
     LGNode pMove = NULL;
     for (i = 0; i < L->numV; i++)
     {
         count = -1; // 除去自身
         pMove = &(L->list[i]);
         while (pMove)
         {
             count++;
             pMove = pMove->next;
         }
         arr[0][i] = i;
         arr[1][i] = count;
     }
 }