前置拣选区存储分配优化

有限开放位置下前置拣选区中新到达物品的存储分配

关键词：存储分配 前置拣选区 仓库

摘要

在电子商务仓库中，补货作业涉及将订单物品从储备区运输到前置拣选区。本文研究在给定拣货订单的前提下，如何在前置拣选区的开放存储位置中存放这些物品（称为新到达的物品），以最小化总行驶距离。先前已存储物品所占用的位置不可用。该问题被建模为一个整数规划，并证明是NP难的。我们提出了一种两阶段分解算法，结果表明该算法能够快速提供高质量的解。与文献中提出的方法及实际使用的方法相比，行驶距离显著减少。此外，我们的数值研究表明，考虑物品先前已存储这一常被忽略的约束条件，可使拣选效率提升超过5%。我们将所提出的算法应用于中国第三方零售商的实际数据，结果表明其性能显著优于该公司当前使用的策略。

1. 引言

仓库，即供应链中两个连续阶段之间的中间设施，在供应链运营中发挥着至关重要的作用（Boysen 等，2019）。特别是，随着过去几十年电子商务和企业对消费者（B2C）分销的快速发展，仓库面临着处理大量小规模客户订单的挑战。这使得订单拣选作业承受了更大的压力，而订单拣选是仓库活动中最耗时的环节。因此，大量研究致力于提高订单拣选的效率也就不足为奇了（例如，参见 德科斯特等，2007）。

由于存在大量小规模订单，许多仓库被划分为前向区域和储备区。在前向区域中，物品以少量存储在易于访问的位置（例如重力流货架，可快速取回物品），而储备区则用于批量存储。在设计前向区域时会出现若干重要的研究问题：确定前向区域的规模、选择应分配的物品以及指定存储位置。针对上述问题，文献中的一个普遍假设是前向区域足够小，以至于拣货员在其中的行走时间可以忽略不计。

然而，由于实际中存在各种区域配置，前向区域的规模不容忽视。例如，前向区域和储备区可以位于同一货架或不同货架上。当它们位于同一货架时，托盘货架的底层作为前向区域，而上层则包含储备存储位置（Bozer, 1985；Thomas 和 Meller, 2015）。在这种配置下，前向区域的规模可被视为与整个仓库一样大。此外，当这两个区域位于不同货架上，前向区域也可能很大，例如，化妆品公司（Velez‐Gallego 和 Smith，2018）的前向区域约60米深，大型鞋类配送中心（Bahrami 等，2019）的前向区域300米长，以及某配送中心的前向区域200米长。因此，拣选人员在这种类型的前向区域中花费的行驶距离不可忽略，并且取决于物品的存储位置。根据 De Koster 等（2007） 和 Gu 等（2007）的研究，订单拣选约占仓库运营成本的55%。在订单拣选活动（如准备、查找、拣取、移动）中，移动是主要组成部分。因此，最小化行驶距离被选为我们的首要目标。

本研究的动机来源于位于中国的一个配送中心。与许多其他电子商务仓库类似，例如德国（魏丁格和博伊森 (2018)）和比利时 （Bahrami et al.(2019)），该配送中心已采用一种策略，即在前向区域以周期性方式顺序进行补货和订单拣选作业。这种方法具有优势，因为它有助于避免（i）待拣物品缺失导致的缺货，以及（ii）在相对较小的前向区域内，包括订单处理设备和人力资源在内的资源之间发生拥堵；这些特点提高了拣选作业的生产效率。

仓储流程详细描述如下。每一次连续的补货和拣选作业称为一个“周期”。在每个周期开始时，可以获得拣货单中订单需求的相关信息。在每次拣选之前，拣选人员首先对前向区域进行补货，以确保所有订单所需的物品均能在前向区域中获得。所需物品集合可分为两个子集：已存储物品和新到达的物品。已存储物品是指先前已放入前向区域的物品，其位置在该周期内保持不变，需对其进行补货以确保数量足以满足订单需求。至于新到达的物品，则未在前向区域中存在，需要从储备区转移过来。实践中，通常采用随机存储策略来存放新到达的物品，这将导致拣货员行驶距离增加。若履行客户订单出现延迟，将对客户满意度中的响应速度产生负面影响。

因此，本研究旨在通过存储分配策略来提升前向区域的运营绩效。

与储备区中的传统储位分配问题（属于中长期决策）不同，前向区域的储位分配问题是一项运营决策，且在每个订单周期中动态变化。首先，每个周期的订单会动态变化，因此每份订单可能包含不同的物品；其次，每个周期开始时已存储物品的数量和种类也各不相同。因此，在不同的补货作业中，新到达的物品也会不同；同时，前向区域中空闲储位的数量和位置在不同周期中也存在差异。

基于此，本文旨在研究以下研究问题：（1）为了最小化给定拣货订单的总行驶距离，新到达物品应被存储在前向区域的哪些位置？（2）相较于文献和实践中常用的储位策略，采用本文提出的算法能够取得哪些改进？（3）所提出的算法在不同路径策略下的表现如何？

尽管大量先前文献关注并研究了存储分配问题，但大多数研究（间接地）假设任何存储位置都可以在无分配限制的情况下使用，例如Boysen 和 Stephan (2013)。关于考虑已存储物品的文献，多数研究采用基于新到达物品与已存储物品之间成对亲和度的聚类与分配分解方法，这种方法在三个或更多物品之间是一种间接甚至不恰当的描述。如第6.1节所示，在订单信息不足（即仅具有成对亲和度）的情况下，与最优解之间的差距显著。此外，目前尚未有研究关注结合考虑已存储物品影响的存储分配方法与路径策略的集成。

本文旨在弥补这一空白。针对所提出的研究问题，本论文的主要贡献如下：（1）提出一种考虑已存储物品的新算法。该算法能够处理前向区域中任意比例已存储物品情况下的优化问题，同时也涵盖了传统空存储布局这一特例。从学术角度提出了两个结构性质以缩小解空间。（2）展示了所提出算法在效率和解的质量方面的竞争力。（3）所提出的算法可推广应用于不同的路径策略（例如，返回、 S形和中点）。在此基础上，我们还探讨了在特定情况下首选的路径策略。这为仓库管理者从管理角度选择路径策略提供了指导。

本文的其余部分组织如下。第2节回顾相关文献。第3节定义并建模新到达物品的存储分配问题。第4节描述一种两阶段分解算法，第5节展示所提出算法的数值结果，并使用实际数据对算法进行评估。理论管理启示在第6节中给出。最后，第7节提出结论和未来研究方向。

2. 文献综述

本文旨在前向区域中做出最优存储分配决策。因此，我们回顾了关于前后备问题和存储分配问题的相关研究文献。

2.1. 前后备问题

关于前后备问题的前期研究非常广泛。正如 Walter 等人 (2013) 所指出，前向区域的性能可能受到以下因素的影响：（1）前向区域的总体规模，（2）存储在前向区域中的物品选择，以及（3）分配给每个物品的数量。 Hackman 等人 (1990) 提出了一种成本模型，用于确定前向区域中物品的分配及其数量。作者提供了一种基于贪婪指数的启发式方法来解决该问题。随后，Frazelle 等人 (1994) 将前向区域的大小视为一个决策变量，并仍然采用了 Hackman 等人 (1990)。巴托尔迪和哈克曼（2008） 扩展了 Hackman 等人 (1990) 的模型，并推导出前向区域中每种物品的最优仓储量，以最小化补货次数。 余和德科斯特（2010） 关注动态存储系统，其中仅将当前拣取批次所需的物品存放在拣取区域，从而显著减少行驶距离。 沙阿和汗佐德（2018） 提出了一种考虑非均匀单元载荷尺寸的动态仓储分配策略，以在长期规划范围内减少仓储浪费。同时开发了一个电子决策支持系统，以实现精益缓冲。

在仓库设计与管理的研究中，前向区域和储备区的运营决策受到的关注较少（德弗里斯等人（2014））。通常情况下，订单拣选和补货作业可以同时或顺序地进行。德弗里斯等人（2014） 制定了优先补货序列的策略，以避免在同步进行拣选和补货作业时发生缺货。然而，在顺序操作下可以完全避免缺货，因为在拣选之前必须先对需要拣取的物品进行补货。苏拉尔等人（2016） 研究了以最小化补货总行走时间为目标的补货序列和补货数量问题，存储分配决策是固定的。江等人（2020） 研究了一个集成的订单拣选与补货协同优化问题，假设使用机器人前置区，他们显式地建模了货架访问次数。与前述研究不同，我们关注的是决定物品在前向区域中存放位置的运营决策，目标是最小化订单拣选作业所需的行驶距离。

2.2. 存储分配问题

存储分配问题涉及确定物品到存储位置的分配，以便能够快速拣取所需物品。有关全面的文献综述，我们建议感兴趣的读者参考 De Koster 等（2007），Gu 等（2007），和顾等人（2010）。不同层次的信息可用性会影响存储策略的选择。如果仅存在当前区域可用存储位置的信息，则随机存储策略是一种直接的方法，其中每个物品被存放在任意存储位置的可能性均等（Hausman et al., 1976; Graves et al., 1977; Yuan et al., 2019）。一旦掌握了物品特定信息，管理者便可采用例如全周转存储和基于类别的存储策略，前提是已知物品的需求信息（余和德科斯特，2009；余等，2015；Guo et al., 2016），在已知各物品在系统中停留时间的情况下采用停留时间存储（’个体停留时间给定的情况下（格尔沙尔克克斯和拉特利夫，1990；Chen et al., 2010；Ang et al., 2012），或利用物品关联性信息进行关联存储，即物品共同出现的频率（李，1992；肖和郑，2010；张等人，2019）。此外，当订单信息完全已知时，相比不完整或有误的订单信息，存储位置可以更高效地重新组织。范奥德赫森登和朱（1992）研究了所有订单均为重复出现时人载式自动化存取系统中的存储分配问题，并为具有一维货架和二维货架且包含不相交和重叠订单的情况提出了算法。随后，Boysen 和 Stephan (2013)通过提供针对不同仓库布局的复杂性证明和贪心算法扩展了该研究。Wutthisirisart 等人（2015）也考虑了给定订单情况下的存储分配，并提出了一种两阶段启发式方法。

潘等人（2015） 在考虑产线平衡和空间分配的情况下，开发了一种基于遗传算法的拣选‐传递系统中的存储分配方法，以提高系统的吞吐量。仿真结果表明，所提出的算法优于以往的分配方法。最近，席尔瓦等人（2020） 将订单拣选问题与存储分配决策相结合，在五种路径策略（即最优、返回、S形、中点和最大间隙）下提出了一种通用变邻域搜索元启发式框架。然而，这些作者假设每个订单仅包含新到达的物品，而在我们的设定中，订单除了包含新检索的物品外，还包含已被需求的已存储物品。因此，拣货路径不仅受新到达物品的影响，也受到同一订单中已存储物品的影响。针对分散存储的订单分批问题，杨等人（2020）通过将物品分配到存储位置、将订单分组为批次，并为给定订单规划拣货员路径，以最小化总拣选距离。在我们的设定中，每个物品也被允许存储在多个存储位置。我们还考虑了已存储物品的影响。有关企业间仓库管理的最新见解，请参见梁等人（2020），他们设计了一个集成云数据库、模糊逻辑和遗传算法技术的系统，可在固定和可变时间窗口批次设置下执行B2B订单预处理。梁等人（2018） 提供了一种混合解决方案，该方案结合遗传算法和基于规则的推理引擎，以提升仓库中的性能。

大多数现有的科学研究间接假设所有存储位置都是可用的。然而，实际情况中，一些物品需要被重新定位，部分存储位置已被占用。因此，我们的研究也与仓库重新分配问题的相关文献有关，其中仅有一部分物品被重新分配以保持仓储作业的高效性。该问题的首次研究由克里斯托菲德斯和科洛夫（1973）开展，他们提出了一种两阶段启发式算法，通过顺序安排物品移动来最小化总行驶成本。

帕祖尔和卡洛（2015）研究了相同的问题，但假设循环物品中的物品按顺序重新分配，且非循环物品必须在循环物品之前重新分配。他们的模型与我们的模型有两个主要区别：（i）本文处理的是运营问题，而他们的问题是在中期规划周期（即季度或每半年）内解决的；（ii）在他们的模型中物品目的地是预先确定的，而在本研究中是决策变量。

阿科尔西等人（2018） 提出了一种针对温敏产品的自适应存储分配策略，旨在兼顾效率与安全库存的管理。为应对需求波动，察米斯等人（2015） 确定了新到达物品的最优存储位置，同时考虑了仓库当前状态以及历史数据。他们还提供了一个案例示例，以展示所提出的存储策略的适应性。此外，蒋等人（2011） 和 庞和陈（2017） 也研究了新到达物品的存储分配问题。由于采用了S形路径启发式算法，且包含至少一个目标物品的通道必须被完全遍历，因此他们将同一通道内的所有可用存储位置视为等同。然而，在本文中，我们考虑了多种路径策略，例如返回、S形和中点策略，因此需要采用一种完全不同的方法论。魏丁格和博伊森 (2018) 研究了分散存储的存储分配问题，其中单个物品分布在货架各处。与那些未考虑未来拣货路线信息的研究不同，我们考虑的是在拣选前即可获取确定性订单集的仓库作业场景。在其他研究中，魏丁格和博伊森 (2018)假设有多个入口连接到输送系统，而我们则考虑单一中央仓库，这在实践中更为常见（德科斯特等， 2007；李等，2017）。

正如我们所提到的，现有文献大多间接假设了一种没有分配限制的存储布局，这实际上是本问题的一个特例，即前向区域中恰好没有已存储物品的情况。此外，我们考虑了实践中常用的几种路径策略，并研究了已存储物品如何影响路径策略的性能。

3. 问题描述和模型构建

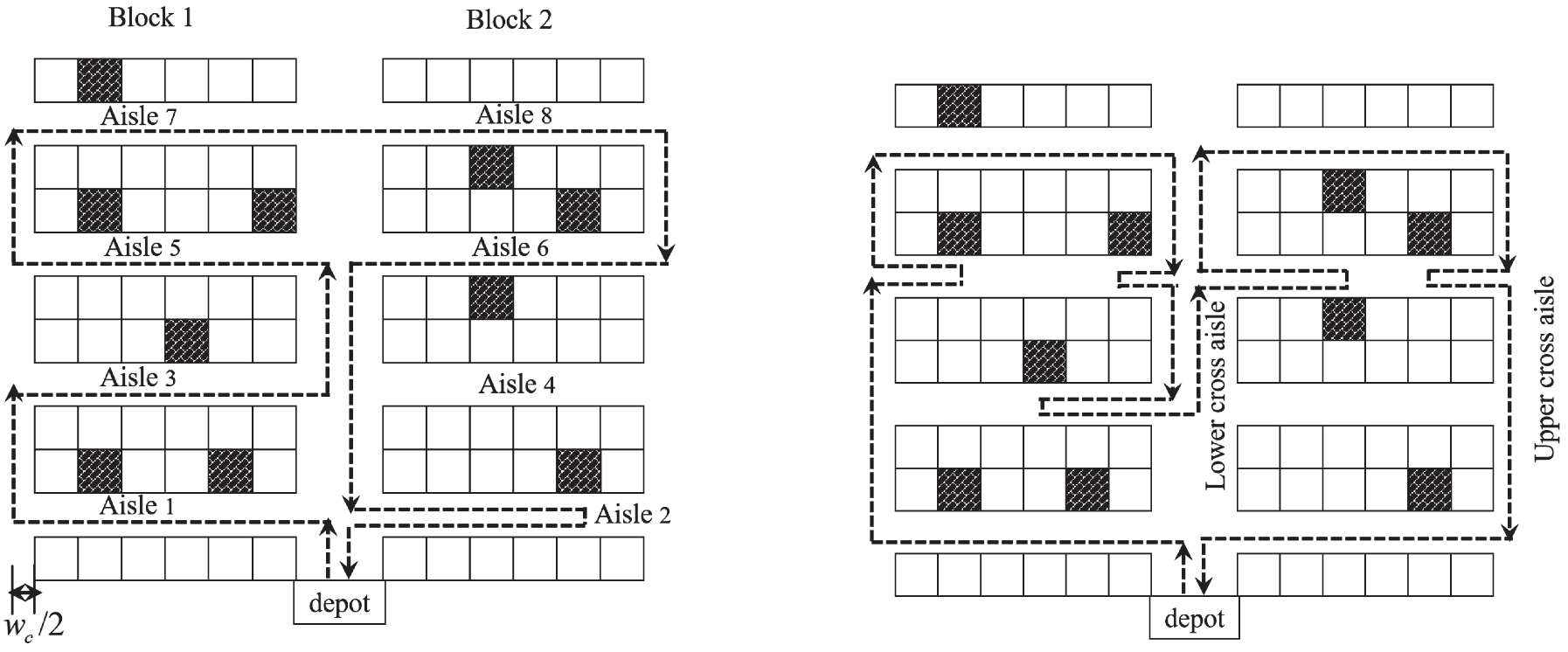
本文集中研究一种矩形双区块布局，其中每个区块包含偶数条平行拣货通道，且存储位置位于通道两侧。设A={1, 2,…| A|}表示通道集合。拣货员从一个通道移动到相邻通道所需的距离为wa。同一通道内两个相邻存储位置之间的距离为wb。中间横通道的宽度为 wc。我们将起点定义为通道与横通道的交点。这种布局在文献中已有广泛研究（勒杜克和德科斯特，2005；拉奥和阿迪尔，2013；德桑蒂斯等，2018），有助于我们清晰地提供管理启示；这些启示适用于实际应用中的任何存储布局。采用返回路径策略，即拣货员从同一拣货通道的同一端进入和离开。所有路径均从中央仓库出发并返回该仓库。

S形策略和中点策略的案例见附录D。

我们现在介绍在返回策略（SAP-NA-Return）下的新到达物品存储分配问题，具体如下。物品集合 SN表示需要从储备区补货的新到达物品的集合。然后，我们有一个开放存储位置集合 L ，这些位置按照距中央仓库的距离递增进行索引。我们需要满足 |L|⩾|SN|， 以便所有新到达的物品都可以被存储。

考虑一个给定的拣货订单集合 O={1,2,…,n}。对于给定的订单 o，设 Ωo 为其包含的物品集合。需要注意的是，物品i∈ Ωo可以是新到达的物品（即 i ∈ SN），也可以是已存储物品。我们忽略仅包含已存储物品的订单，因为完成此类订单的行驶距离是固定的，无法进行优化。我们假设每个订单 o ∈O 中至少存在一个新到达的物品。SAP-NA-Return的目标是将新到达的物品分配到开放存储位置，以在返回路径策略下最小化给定拣货订单的总行驶距离。

例1： 考虑 所示的布局。) 共有16个存储位置，每个位置用一个方块表示。带有标签“item i”的灰色方块表示物品i的存储位置，其中i = 5,…,14。我们暂时使用符号A、B、C、D、E和F来表示六个空闲储位，这些空闲储位以白色方块表示。此外，有四个新到达的物品（编号为1到4）需要存放，并有九个订单将被依次处理。订单的详细信息如 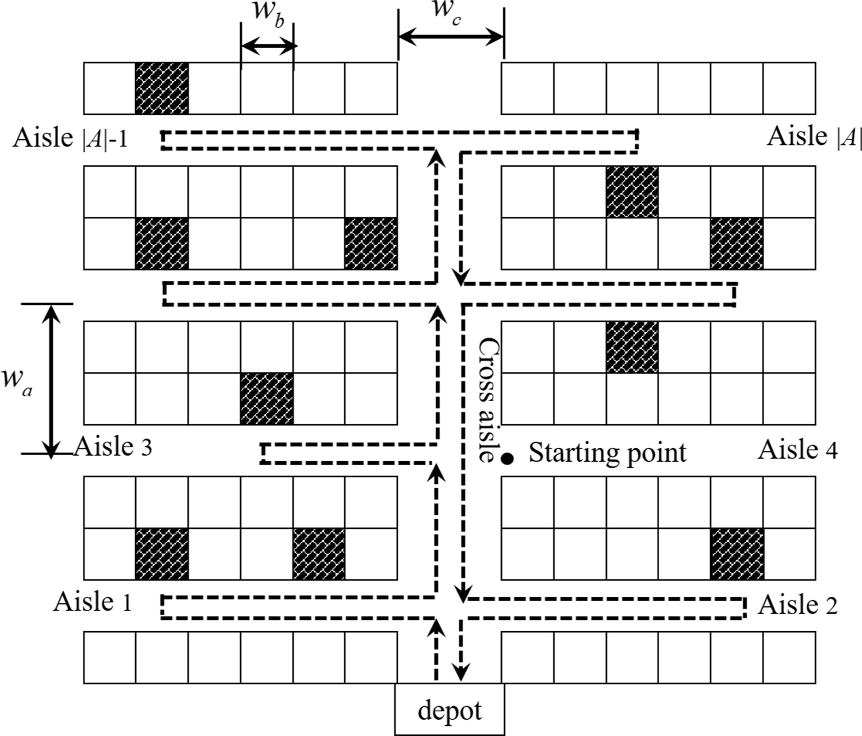所示。) SAP‐NA‐Return的一个可行解是将物品1、2、3和4分别分配到位置A、B、C和D。

在建模问题之前，我们详细说明SAP-NA-Return问题中包含的属性和假设（符号说明见表1）：

• 所有存储位置大小相同，且每个位置仅存放一种类型的物品（Boysen和Stephan，2013；Wutthisirisart等，2015）。我们还可以通过引入额外的参数Dis j来表示中央仓库与位置 j之间的距离，以考虑不同位置的尺寸差异。
• 我们仅关注订单拣选过程中的距离最小化，而忽略了补货过程的影响。这是因为订单拣选过程更加时间紧迫且劳动密集（德科斯特等，2007），而补货整个前向区域有充足的时间。
• 客户订单已经过批次划分并已知，如第1节所述。补货过程在拣选作业开始之前进行，这意味着所有所需物品都将从前向区域拣取。
• 拣选人员可以够到所有物品，无论货架高度如何，因此忽略在货架不同层之间上下移动进行拣取的垂直移动。
• 每个新到达的物品仅被分配到一个开放存储位置。如果放宽此假设，我们可以将该物品拆分，并在问题中将其视为多个独立的物品。当每个物品所需的存储位置数量已知时，该方法可行。一旦每种物品的位置数量成为一个决策变量，这给我们的研究问题增加了相当大的复杂性，超出了本研究的范围。我们将此类扩展留给未来研究。

A应用表1中总结的SAP-NA-Return符号说明，问题可表述如下 .

SAP − NA − 返回 : 最小化Z = ∑∑y WA oa +y CA o ,
o∈Oa∈A s.t. ∑xij ≤ 1 ∀j ∈L,
i∈SN∑xij= 1 ∀i ∈ SN,
j ∈L y WA oa ⩾2(djxij+w c 2) ∀i ∈ Ωo⋂SN; ∀o ∈O; ∀j ∈La; ∀ a ∈A,
y WA oa ⩾2(boa+w c 2) ∀o ∈O; ∀a ∈A,(2 ⌈a /2⌉ − 1)wa⩽y CA o +M(1 − uoa) ∀o ∈O; ∀a ∈A,∑u oa= 1 ∀o ∈ O,
a∈A zoa⩾uoa ∀o ∈ O; ∀a ∈A,
zoc⩽1 − uoa ∀ o ∈O; ∀c ∈{a+1, …, A}; ∀a ∈A,
boa⩽Mzoa ∀o ∈ O; ∀a ∈A,
zoa⩾xij ∀i ∈ Ωo⋂SN; ∀o ∈O; ∀j ∈La; ∀a ∈A,
xij ∈{0, 1} ∀i ∈SN; ∀j ∈L,
zoa, uoa ∈{0, 1} ∀o ∈O; ∀a ∈ A,

目标函数(1)最小化给定拣货订单的总行驶距离。约束条件(2)和(3)分别确保每个开放存储位置至多接收一个物品，且每个新到达的物品都被分配到一个开放存储位置。完成每个订单的行驶距离由约束条件(4)–(6)确定。因此，通道内行驶距离为每条通道的通道内距离之和。我们允许yWA oa = 0 if在拣取订单o时未访问通道a。对于订单o，每条通道的通道内行驶距离取决于最远的拣取位置，该位置要么是到已分配物品i,i ∈ Ωo⋂SN的开放存储位置的距离（约束条件(4)），要么是朝向属于订单o且已存储在某些位置的物品的最远通道内距离（约束条件(5)）。跨通道行驶距离取决于包含需访问物品的最后一通道，如约束条件(6)所示。由于我们在目标函数中最小化yCA o ， 因此无需限制其上界。约束条件(7)保证每个订单o仅存在一个最后一通道。在约束条件(8)和(9)中，如果a是包含订单o中物品的最后一通道，则z oa =1且∑ A = c a+1zoc = 0。约束条件(10)确保如果boa 大于零，则z oa 被设为1，即必须访问通道a。约束条件(11)表明当使用开放位置j时，其对应的通道必须被访问。最后，约束条件(12)和(13)定义了变量的可行域。M可分别用(2 ⌈|A|/2⌉ − 1)wa 和maxa∈A {boa}替代约束条件(6)和(10)中的上界。

对于某些已存储物品，可能会出现前向区域中的库存不足以满足订单需求的情况。针对此情况，我们将包含该物品的订单分为两组：一组使用当前（已存储）库存来满足，另一组则使用新到达的库存来满足。也就是说，后一组订单所需的该物品被定义为需要补货的新到达物品。为解决此问题，需要明确哪些订单应由当前库存满足。我们根据以下规则确定这些订单：考虑一个已存储的物品i，其位于通道a中的存储位置j处，且其当前库存CI i 小于所需订单数量RO i 。然后我们可以确定集合O′ i ={o⊆O : i ∈Ωo , b oa =∕ d j }，该集合包含所有至少有一个所需物品已存储在通道a中且存储位置比位置j更远的订单。如果 |O ′ i |⩾CI i ，则可以从O′ i中随机选择CI i 个订单， 并使用已存储库存来满足这些订单。如果 |O ′ i | <CI i ，则需要从其余订单中选择CI i − |O ′ i | 个订单由当前库存满足。为此，可以按照任意一个所需已存储物品与已存储物品i之间的最小行驶距离对所有剩余订单进行排序。接着需要考虑以下两种情况：i) 若排序后的订单数量（记为 |O ′′i | ）不少于CI i − |O ′ i | ，则将前CI i − |O ′ i | 个订单分配给由已存储库存满足的组根据当前库存。ii) 如果 |O′ ′i |< CIi − |O′ i |，即我们需要将 CIi − |O′ i | − |O′ ′i |个订单分配给该组。我们根据订单规模对需要物品 i 的剩余订单进行排序，并将规模较小的订单分配到该组中。然而，我们无法证明上述规则能够得到最优解。此类扩展将留待未来研究。

接下来我们确定 SAP-NA-Return 的计算复杂度。我们将强NP难的产品定位问题（PLP，Boysen 和 Stephan (2013)）归约到我们的问题。给定一个订单集合 O ，每个订单需要从总物品集合 S 中获取特定的子集物品，PLP 的目标是将物品分配到一条直线上的存储位置，使得每种物品恰好获得一个存储位置，并最小化给定拣货订单的总行驶距离。我们构造一个 SAP-NA-Return 实例，其中仅考虑一个通道且 SN=S ，以便所有物品都需要补货。我们的目标是最小化给定订单 O 的总行驶距离。显然，这两个问题之间存在一一对应关系。因此，我们的 SAP-NA-Return 问题也是强NP难的。

由于在合理时间内找到 SAP-NA-Return 最优解的计算难度较大，第 4 节提出了一种启发式算法，以在合理时间内获得解。此外，附录A中提出了一种用于确定下界的算法，可用于评估所提算法的性能。

4. 求解方法

所提出的算法基于以下观察：对于给定的开放存储位置，物品‐位置分配问题可通过动态规划方法最优求解。因此，采用了一种“先选址后分配”两阶段分解算法，其中所需的开放存储位置根据两个优先规则（第4.1节）进行选择，随后获得物品到位置的最优分配 （第4.2节）。接下来将讨论该算法的详细内容。

4.1. 优先规则

首先，以下命题1 陈述了一种支配性质，以减少空闲储位选择的搜索空间’的选择。

命题1。 （1）设j1和j2为两个开放存储位置，它们位于同一通道，且dj 1 < dj 2 。如果在最优解中选择了j2 ，则j1也在最优解中。（2）设j1和j2为两个开放存储位置，它们分别位于不同的通道a1和a2, ，其中a2> a1。对于任意新到达的物品i，若{o:o⊆O,i∈Ωo} [max(boa 2 , dj 2) +boa 1 − max(boa 1 ,dj 1) − boa 2]⩾0成立，且j2被选入最优解，则j1也在最优解中。

证明见附录B。接下来，我们引入两种优先规则，这些规则在初步测试中表现高效，用于选择开放存储位置。回顾新到达物品的数量为|SN|。因此，由于存在一对一对应关系，所需开放存储位置的数量也必须是|SN|。

第一个优先规则是一种基于位置的规则（以下简称LOR）。它选择距离中央仓库最近的|SN|个空闲储位，该方法因操作简便而在实践中被广泛使用。然而，LOR仅考虑了地理位置的影响，未能充分利用订单信息。

第二个优先规则是基于订单的规则（OOR）。它考虑了订单信息，其依据如下观察：对于订单o ，在通道a内的行驶距离要么是到属于开放存储位置集合L中的某个开放存储位置的通道内距离，通道 a，或订单 o 中包含的已存储物品在通道内的最远距离，即 y WA oa =最大值{boa ,d j} + w c 2 ,j ∈开放存储位置集合 a。为了最小化通道内行驶距离，我们优先选择满足 j 且 dj⩽ b oa 的开放存储位置。定义 goj ={1 ifd j ⩽b oa ，j ∈开放存储位置集合 a ，0否则. , 并令G j =∑o∈O g oj为空闲储位 j的值。然后，我们为该问题选择具有最高G j值的 |S N |个空闲储位。

示例（续）： 对于 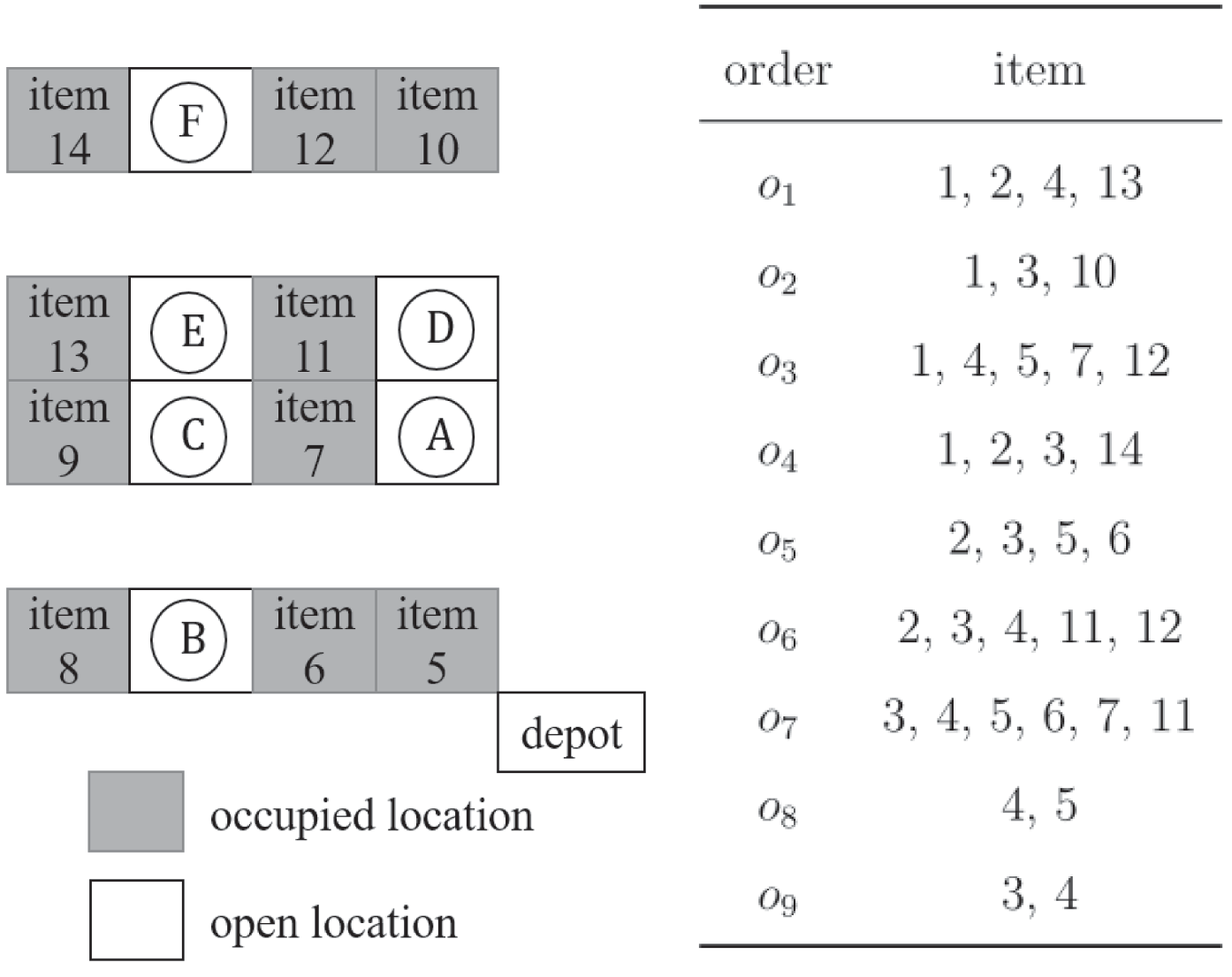基于LOR所选的开放存储位置集合为{A,B,C,D}。就OOR而言，我们可以根据{o3 , o5 , o7 , o8} 推导出G 1 = 4 ，并根据{o1 ,o2 ,o3 , o4 ,o6 ,o7} 推导出G 4 = 6 。同理，可得G 2 = 1、G 3 = 1、G 5 = 2和G 6 = 2。因此，基于OOR所选的开放存储位置集合为{A,D, E, F}。

4.2. 在给定开放位置的情况下寻找最优分配策略

在本节中，我们首先提出一种动态规划（DP）方法，以在预先确定的空闲储位集合下，求解新到达物品的最优分配。然后引入一种束搜索（BS）方法以提高求解效率。

4.2.1. 动态规划方法 The DP decision

该过程被划分为|SN | +1个阶段，其中每个阶段p = 1，…|SN |表示由第4.1节中的优先规则选定的一个开放存储位置。所选的开放存储位置按距仓库的距离递增排序。此外，令p = 0为起始阶段0。在第p阶段的状态V表示已分配到距离仓库最近的前p个开放存储位置的新到达物品的一个子集V，V⊆SN ，|V| =p。第p阶段的状态数量等于二项式系数(| S N | p )。

我们首先定义两种类型的订单集合，用于计算部分目标。第一种类型是O V ，包含订单集合不包含状态V中未分配项目的订单集合，即 {OV ∈O : (SN⋂ΩOV) − V = ∅}，其中SN⋂ΩOV是订单OV中新到达的物品集合。例如，假设总物品集合和新到达物品集合分别为 S ={1, 2, 3, 4, 5} 和 SN={1, 2, 3}。我们考虑状态 V ={1, 2}。对于订单 o1={2, 4}，由于 S N⋂Ωo1 − V ={2} −{1, 2, 3} = ∅，因此有 o1⊆O{1,2}。然而，订单 o2={1, 2, 3, 5} 不包含在 O{1,2} 中，因为该订单中存在未分配的物品 3。实际上，对于每个状态V，基于需访问的给定存储位置，可以准确确定在订单集合OV上的行驶距离。另一种类型的订单集合是 OV,i， 它是OV的子集，包含新到达的物品i，即 {OV,i ∈O : (SN⋂ΩOV) − V = ∅,i ∈ ΩOV}。我们将使用 OV,i 来计算转移值，这将在下文介绍。

状态V的目标由f(V)表示，其代表完成OV所产生的最小行驶距离。随后，定义从状态V′到状态V的转移，当且仅当V′⊂V且V − V′= i ，其中i ∈ V 。此类转移所关联的额外行驶距离记为c(V,i)，其计算方式为c(V,i) =∑o∈OV,iTRo，其中TRo为完成订单o的行驶距离。该递归可形式化如下：
f(V)= mi∈iVn{f(V −{i})+ c(V,i)}, (14)
其中f(∅) = 0。此处，为|V|个物品寻找最优分配的问题可分解为：从V 中选择单个物品i ，并结合对|V −{i}|个物品在先前存储位置1,…,|V −{i}|上的最优分配问题。最后，当达到最终阶段并确定最优解值f(V)时，可采用简单的逆向递推来找到最优分配。

总之，我们有 2|S N | 个状态和 |SN |2|S N |− 1 次转移。每次转移都需要检查所有 n 个订单，在最坏情况下这些订单包含 |SN| 个新到达的物品。这意味着总的计算复杂度为 O(n |SN |22|S N |)。

示例（续）： 考虑 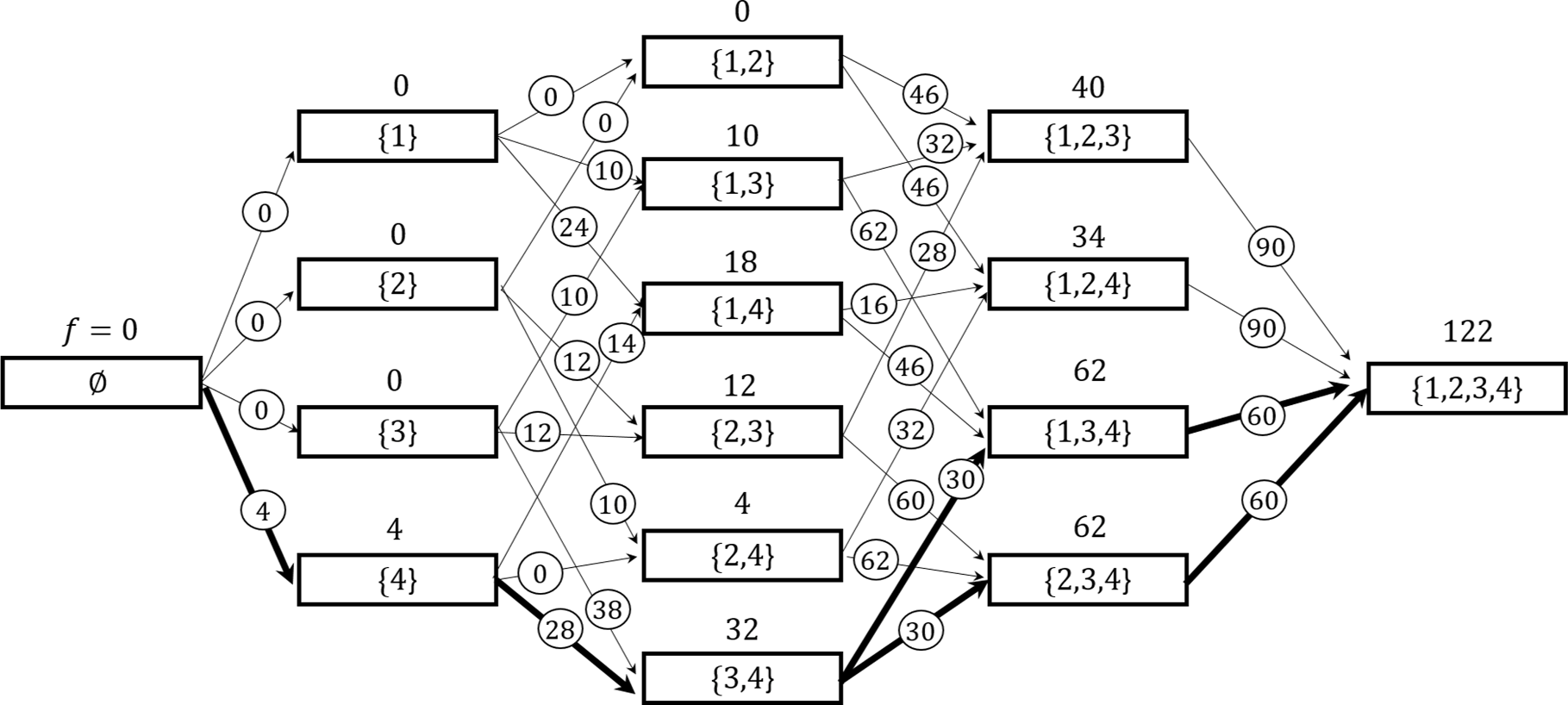以及给定的开放存储位置集合{A,D,E,F}。参数wa= 1,wb= 2和wc= 5已知。对应的动态规划图 及对应于加粗路径的最优解，其最佳目标值为f=122，如

4.2.2. 束搜索方法 束搜索方法减少了需要构建的状态数量；我们采用该方法以提高求解效率。该过程的详细信息见算法1。

算法1。束搜索方法
1: 初始化：从阶段0开始，构建阶段1中的所有状态。
2: for p= 1,…|S N | do
3: for状态 V在阶段 p do
4: 计算状态 V的目标值 f(V)。
5: 计算状态 V的下界值 LB(V)。
6: end for
7: 将阶段 p中的所有状态按值 f(V) + LB(V)的非递减顺序排序。
8: 仅扩展前 ξ个状态，并分支以构建阶段 p+ 1中的分支状态集合。
9: end for
10: 返回最终阶段 p= |SN|中的最优解。

BS算法在每个阶段仅对ξ （波束宽度）个最有前景的状态进行分支，从而减少了计算时间和内存。然而，这样做意味着我们的算法不能保证达到最优解。每阶段最有前景的ξ个状态根据f(V)+LB(V)（步骤7）进行选择，其中f(V)是第4.2.1节中所示当前状态V的最优目标值，LB(V)是状态特定的下界。LB(V)的值可通过为每个尚未确定的订单o单独计算最小行驶距离so获得，即{o ∈ O : o⋂O V= ∅}，然后将这些值相加。计算so的思想基于未分配的新到达物品被假定分配到下一个“最佳”开放存储位置，以使订单o的行驶距离最小化。只有最有前景的状态被扩展，以构建下一阶段的状态集合（步骤8）。我们重复这些步骤，直到达到最终阶段（步骤10）。

可通过一个简单的递归找到最优分配。

从第一阶段到第二阶段需要评估 |SN| 个转移，从阶段 k 到阶段 (k+ 1), k= 2,…|SN| − 1 共有 ξ(|SN| −(k − 1)) 个转移。因此，总共有 ξ|SN|(|SN|− 1) 2 个转移。每次转移都需要检查所有 n 个订单，在最坏情况下，每个订单的下界可以在 O(n |A|2 |SN |4) 时间内计算（见 附录 A）。因此，总计算复杂度为 O(ξn |A|2 |SN|4)。

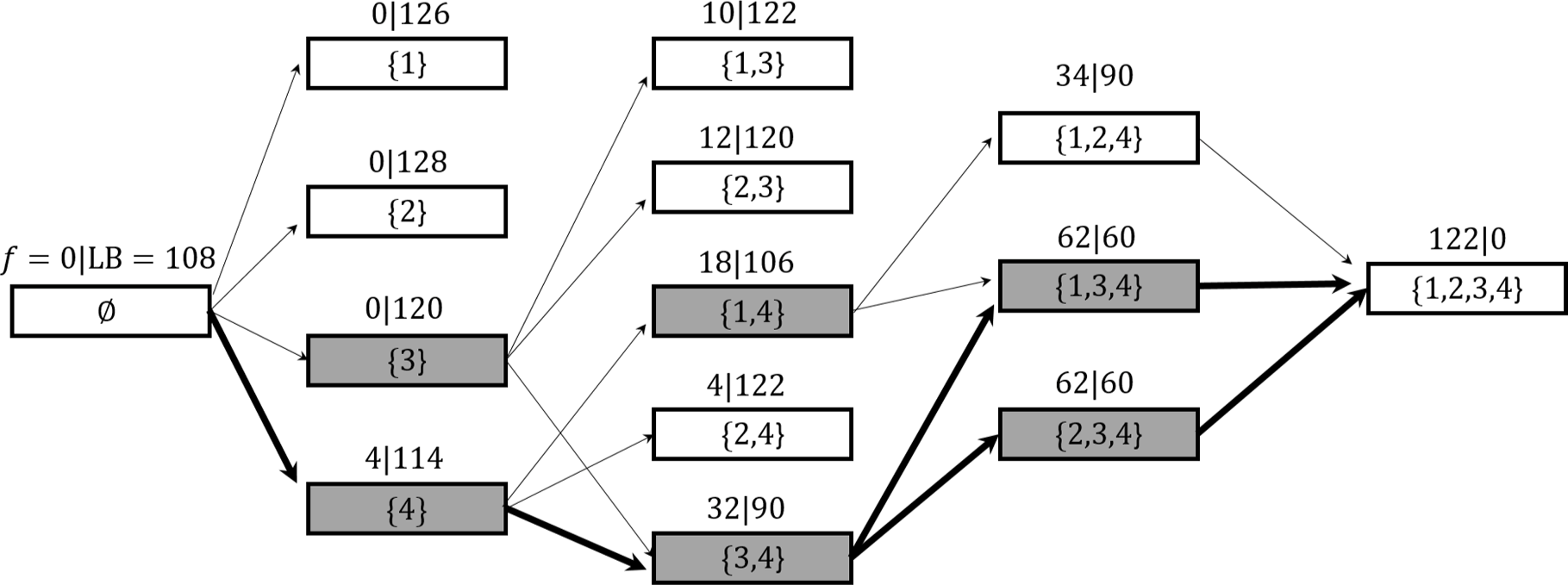
示例（续）： 再次考虑 以及给定的开放存储位置集合{A,D,E,F}。束搜索图在ξ= 2时如![图4](图4. 例1在
所示，其中灰色方块表示待构建的状态。获得的最优目标值为122，与动态规划过程得到的值相同，但计算复杂度显著降低。

通过利用支配规则，可以增强束搜索的效果。我们首先通过一些启发式方法确定一个全局上界UB ，例如全周转存储策略，或先前文献中提出的策略（例如，第6.1节）。然后，以下命题建立了支配规则，以剪枝被支配的部分状态。

命题2。 (1) 当f(V) + LB(V) > UB时，状态V可以被剪枝。(2) 设V⧹{i1}和V⧹{i2}为阶段|V| − 1中的两个状态。如果f(V⧹{i1})⩽f(V⧹{i2})， 且i1和i2在订单中始终同时出现，则状态V⧹{i1}支配状态V⧹{i2}。

证明见附录C。考虑 使用Wutthisirisart 等人（2015）提出的最小延迟算法，上界 等于123。在状态{1,4}中，我们有f({1,4})+ LB({1,4})= 124>上界。因此，根据命题2，状态{1,4}可以被剪枝。

5. 数值实验

在本节中，第4节介绍的算法通过若干计算实验进行测试。第5.1节给出了实例生成的详细信息。第5.2节展示了所提出算法的性能。第5.3节基于从中国的一家第三方物流服务提供商收集的数据进行了实际案例研究。

所有算法均使用 Matlab R2018a，运行在Intel Core i5‐8250 CPU、1.6 GHz主频和8 GB内存的环境下，运行64 bit Windows 10。 SAP-NA-Return由CPLEX 13在Matlab中使用concert框架YALMIP编码求解。

5.1. 实例生成

我们研究了计算 两种规模问题实例的性能：可求得最优解的小规模实例 n

5.3.1. 案例公司的当前运营In each cycle, the replenishment and picki

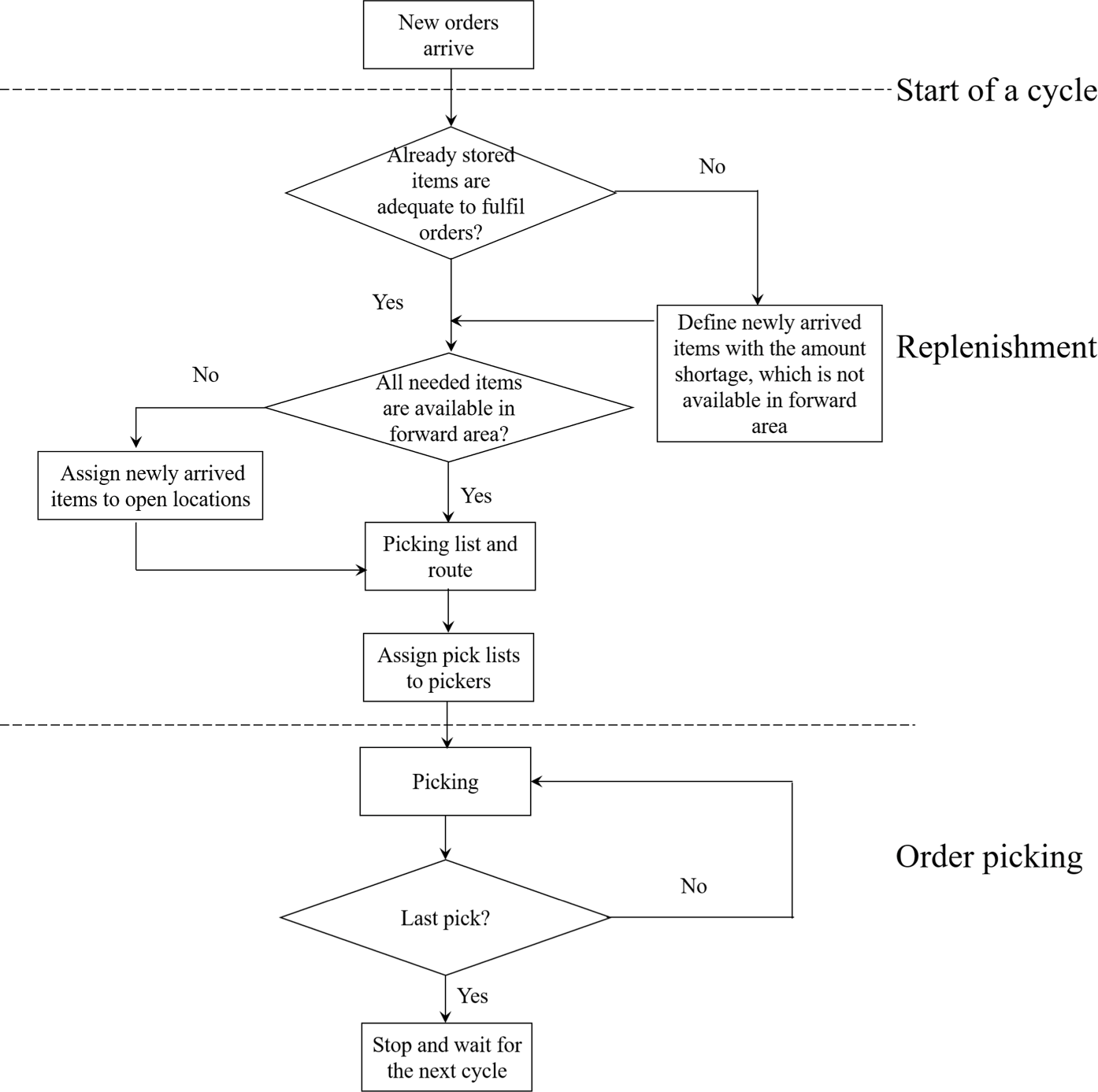
ng processes are performed sequentially in a cyclic manner, as shown in Once acycle starts, the pickers replenish each item needed in the forward area from reserve storage to guarantee availability, usually takingone hour. Then, order picking needs to be completed in a short time(i.e., one hour). Since the customer orders are often small in sizeand high in variability, the order picking becomes a much more labor-intensive process. According to the manager’s opinion, the timesaved for order picking is more valuable than the time for replenishment. During a cycle, new orders are gathered based on the first-

表3小规模实例在不同参数设置下的计算性能。
| α | |O| | CPLEX | DP | BS |
| :— | :— | :— | :— | :— |
| 0.2 | 50 | −/3.02%/1.45 | 0%/3.02%/0.9 | 0.51%/3.52%/0.6 |
| 0.2 | 100 | −/3.31%/9.32 | 0%/3.31%/1.39 | 0.81%/4.10%/1.11 |
| 0.2 | 200 | −/3.97%/30.79 | 0%/3.97%/2.51 | 0.42%/4.33%/2.18 |
| 0.3 | 50 | −/4.49%/552.78 | 0%/4.49%/34.38 | 1.95%/6.38%/1.21 |
| 0.3 | 100 | −/5.04%/2484.82 | 0%/5.04%/35.74 | 1.28%/6.27%/2.48 |
| 0.3 | 200 | 内存不足 | −%/7.02%/44.44 | 2.11%/8.93%/4.66 |
| 0.4 | 50 | 内存不足 | −%/4.84%/2856.58 | 2.05%/6.78%/2.21 |
| 0.4 | 100 | 内存不足 | −%/5.29%/2967.22 | 1.92%/7.08%/4.63 |
| 0.4 | 200 | 内存不足 | −%/6.06%/3247.51 | 1.25%/7.25%/8.97 |

注：对于“CPLEX”列和“DP”列，符号“a/b/c”表示“与CPLEX的平均差距/与下界的平均差距/平均CPU时间(秒)”；对于“BS”列，符号“a/b/c”表示“与 DP的平均差距/与下界的平均差距/平均CPU时间(秒）”。

表4大规模实例在不同参数设置下解的计算性能。
| α | |O| | LOR + BS算法 | OOR + BS算法 | CPU时间(秒) | CPU时间(秒) |
| :— | :— | :— | :— | :— | :— |
| | | 无剪枝 | 有剪枝 | | |
| 0.2 | 50 | 2.18%/3.56% | 1.45% | 34.47 | 20.19 |
| 0.2 | 100 | 4.78%/7.28% | 2.71% | 67.64 | 44.29 |
| 0.2 | 200 | 5.01%/8.61% | 3.78% | 108.92 | 81.93 |
| 0.5 | 50 | 5.47%/8.17% | 2.88% | 114.82 | 90.89 |
| 0.5 | 100 | 5.99%/9.01% | 3.17% | 185.24 | 133.76 |
| 0.5 | 200 | 5.47%/9.34% | 4.29% | 310.31 | 224.47 |
| 0.8 | 50 | 6.19%/10.86% | 5.12% | 207.69 | 163.82 |
| 0.8 | 100 | 6.45%/11.98% | 5.89% | 351.47 | 277.74 |
| 0.8 | 200 | 7.23%/14.01% | 5.96% | 656.83 | 489.78 |

注：对于“LOR + BS”列，符号“a/b”表示“与OOR + BS的平均差距/与下界的平均差距”。对于“OOR +BS”列，符号“‐/b”表示“‐/与下界的平均差距”.

5.3.3. 存储分配程序We developed a storage assign 嵌入仓库管理系统的管理程序。 采用存储分配算法OOR的循环流程图+ BS。我们通过两个关键性能指标来监控其性能：行驶距离和延迟订单数量。假设平均速度为 1.1 米/秒，这是拣货员典型的步行速度（Bottani 等人，2012）。由于订单按照先到先服务规则处理，因此可以得到每个订单的完成时间。在每个周期中，若订单未在相应的拣货时间窗口内（例如第一个周期中的9:00–10:00）完成，则称为延迟订单。请注意，空闲储位并非随机生成，而是由先前周期中处理订单的结果所决定。

5.3.4. 数值模拟We verify the feasibility

以及通过数值模拟评估OOR + BS的有效性。关于行驶距离的计算结果如 所示。在所有周期中，OOR + BS均显著优于随机存储，平均改进为10.74%。表5 展示了延迟订单数量方面的性能，突显了OOR + BS的优势。与随机存储相比，它将延迟订单的平均数量从10.5减少到0，能够有效解决响应速度问题。

6. 管理启示

在本节中，我们探讨管理层面的问题，以期为仓库管理者提供决策支持。首先，在第6.1节中，我们将所提出的OOR + BS算法与几种流行策略进行了对比测试。接着，在第6.2节中，我们探讨了两个阶段的影响：使用优化的空闲储位选择替代随机选择，以及采用优化的货物存储分配替代随机存储分配。此外，在第6.3节中，我们重点关注不同的路径策略，包括返回、S形和中点策略，以系统地验证在何种情况下哪种路径策略最优。在第6.4节中，我们研究了考虑先前已存储物品影响的价值，这一因素在文献中常常被忽略。最后，在第6.5节中，我们讨论了本研究的实际意义。

6.1. 将OOR +BS与其他策略进行比较

在本节中，我们将所提出的算法OOR + BS与流行策略进行比较，例如随机存储(RND)、全周转率存储(FT)、最小延迟算法 (MDA, Wutthisirisart 等人（2015）)以及基于关联规则的仓储(ARB, 庞和陈（2017）)。RND因其对存储位置的高效利用而被广泛使用。它将新到达的物品随机分配到一个开放位置。FT根据流行度（即包含该货物的订单数量）将每个新到达的物品分配到最近的开放位置。MDA和ARB的选择是基于Wutthisirisart 等人（2015） 和 庞和陈（2017）所展示的有效性能。在MDA中，第一阶段生成一个物品线性序列，以最小化拣货过程所需的线性行驶距离；第二阶段根据该线性序列将每个新到达的物品分配到一个开放位置。ARB提出了一种新的关联指数，用于评估新到达的物品与未分配的存储位置之间的适应度。

具体而言，我们考虑包含100个订单{0.1,0.3,0.5,0.7,0.9}的大规模实例。对于每个α ，我们为100个实例随机生成订单，并报告平均目标值。如表6所示的结果表明，OOR + BS在目标值方面显著优于所有这些策略。当新到达的物品数量较多时（即α= 0.9），其平均行驶距离比RND缩短超过45%，比FT缩短6%，比MDA缩短8%，比ARB缩短38%。当新到达的物品较少时（向α= 0.1和0.3移动），其他四种策略表现良好，但仍平均比OOR +BS差5%。原因是更多的灵活存储位置能够带来更大的改进空间，而开放存储位置较少时，最小化行驶距离的机会则更小。此外，ARB和FT的结果均显示出与OOR + BS存在高偏差。可以得出结论：当使用较少的订单信息（例如仅成对项目相关性或仅项目周转率）时，与最优解之间的差距更大。

表5使用实际数据时我们的算法在延迟订单方面的性能。
| 策略 | 周期中的延迟订单 | | | | | | | | Mean |
| :— | :— | :— | :— | :— | :— | :— | :— | :— | :— |
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 随机存储 | 13 | 10 | 20 | 29 | 4 | 0 | 8 | 0 | 10.5 |
| OOR + BS算法 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |

表6OOR + BS 与四种策略的启发式算法解值之间的解改进情况。
| α | ImpRND OOR+BS算法 (%) | ImpFT OOR+BS算法 (%) | ImpMDA OOR+BS算法 (%) | ImpCOR OOR+BS算法 (%) |
| :— | :— | :— | :— | :— |
| 0.1 | 5.18 | 3.67 | 6.10 | 4.27 |
| 0.3 | 7.34 | 4.47 | 6.83 | 8.12 |
| 0.5 | 10.65 | 7.88 | 7.37 | 9.37 |
| 0.7 | 33.26 | 8.99 | 7.92 | 25.12 |
| 0.9 | 41.89 | 9.23 | 9.18 | 36.47 |
| 总体 | 19.67 | 6.81 | 7.48 | 16.67 |

注：改进值按 Impb a(%) =((b − a)/b) × 100 计算。

表7三种方法相较于OOR α= 0.2/0.5/0.8的性能提升 + BS算法。
| 第一阶段 | 随机 | OOR |
| :— | :— | :— |
| 第二阶段 | | |
| 随机 | 6.80%/16.23%/30.78% | 6.10%/18.23%/32.56% |
| BS | 3.76%/5.01%/6.88% | –/–/– |

6.2. 阶段的影响

接下来，为了探究两阶段算法中每个阶段对总体性能的性能提升，我们比较了以下三种方法：(i) OOR +随机：第一阶段进行优化，而在第二阶段采用随机存储策略。(ii) 随机 + BS：仅对第二阶段进行优化，可用存储位置的选择随机确定。(iii) 随机 +随机：两个阶段均不进行优化。与OOR + BS相比，大规模实例的目标值在百分比上的相对降低情况如 表7 所示。这些结果得出以下发现：

• 仅优化开放存储位置的选择（第一阶段）无法提升算法的性能’。这是因为OOR + BS算法根据订单信息进行工作，而这还依赖于解决货品‐存储位置分配问题（第二阶段）。如果不对第二阶段加以关注，第一阶段的努力将白费。事实上，对于 α= 0.5和0.8， OOR +随机 的表现甚至比 随机 +随机 更差。
• 仅优化存储策略（第二阶段）将带来显著的性能提升，因为它利用了订单信息。因此，我们建议管理者更加关注物品‐存储位置分配问题的优化。然而，通过在第一阶段使用我们的优先级方法，还可以额外获得超过4%的性能提升。
• 随着α的增加，改进程度也随之提高。这是由于可以重新组织更多物品的存储位置，这当然会更加高效。

6.3. 不同的路径策略

只有在已知路径策略的情况下，才能评估存储分配决策，而订单中待拣取物品的相对位置会影响拣货路径。因此，存储分配问题与路径问题被整合在一起。本研究针对新到达的物品，在三种常用路径策略——返回、S形和中点——下进行存储分配，以探究在何种情况下应推荐哪种路径策略。其中两种路径策略的模型公式见附录D。尽管第4节提出的两阶段方法可以快速推广应用于新的路径策略，但在解的质量方面不太可能与元启发式算法相竞争。因此，我们还提出了一种遗传算法(GA)。两阶段方法以及遗传算法(GA)的详细信息也在附录D中介绍。

我们的计算实验设计如下：生成包含100个订单的大规模实例。对于遗传算法，我们设置最大值= 50,ρ= 0.8, 以及ϱ= 0.15。具体而言，研究了以下三个参数： (i) 前向区域的形状：给定所有通道内的存储位置总数，过道数量越多，跨通道行驶距离越长，而通道内行驶距离越短。

• 首先，返回策略在具有长通道（| A| = 6和10）、拣选次数少（MaxSize= 4和6）以及访问通道少（θ= 0.2）的情况下，是最佳的路径规划方法，实验结果如所示。其原因是，在这些场景下，返回策略能够缩短通道内的行驶距离。当物品仅位于一个通道内，或分布在多个靠近前横通道位置的通道内时，执行返回操作比完全穿过通道更高效。
• 其次，当大量拣选分布在仓库中时，S形路径策略优于其他两种路径策略。当MaxSize较高（趋近于MaxSize= 8和10）时，位于通道更深处的物品更有可能被需求。此外，需要访问的通道数量越多（θ=0.8），完全穿过通道的优势就越明显。
• 最后，中点路径策略在订单规模和访问通道数量既非非常小也非非常大时表现更优。可能的原因包括本列表前面几项中先前讨论过的内容。此外，中点策略的表现不受通道数量的影响。

6.4. 已存储物品的影响

最后，我们研究考虑某些位置因被已存储物品占用而无法使用的约束条件所带来的价值。考虑以下“基准测试”算法：首先，我们忽略该约束，假设前向区域中的所有位置均可使用。然后，根据我们提出的两阶段算法分配新到达的物品。设rri为存储新到达物品i的存储位置。然而，该解有时是不可行的，因为rri可能已被某个已存储物品占用。因此，这些“不可行”的新到达物品的解必须重新分配。我们的问题是，在所有“不可行”的新到达物品中，最小化从上述方法确定的当前存储位置到所有可能的开放存储位置的总移动距离。该问题可通过基于匈牙利方法的线性分配问题在多项式时间内求得最优解。最后，我们将所提及方法获得的结果与我们的两阶段算法进行比较。

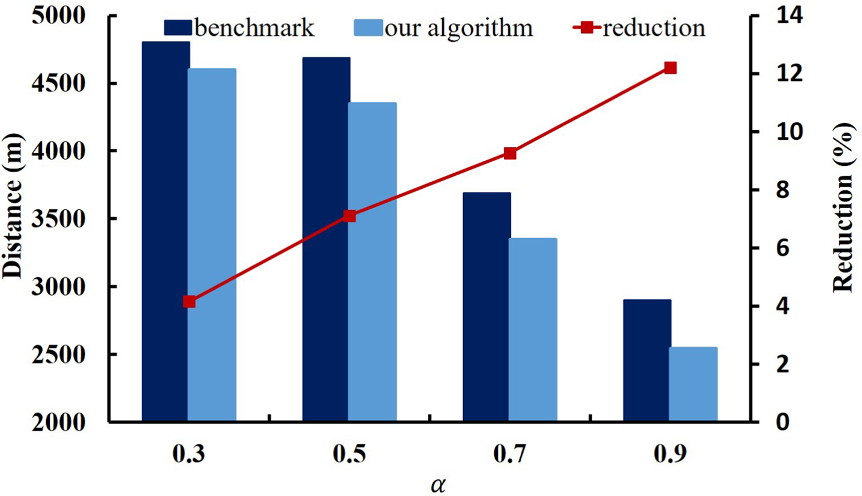
假设已存储物品事先在前向区域中随机存放。 展示了OOR+ BS算法与基准测试之间的比较，其中每个实例重复十次以生成平均值。结果表明，OOR+ BS算法在不同情况下优于基准测试，距离减少达到5%至13%。回顾表6中的结果，我们的算法比完全周转策略（FT）高出3%至9%。这意味着忽略已存储物品的影响将导致性能低于流行的完全周转策略。因此，强烈建议管理者在决策时考虑已存储物品的影响。

6.5. 应用与实际意义

实验和实践结果表明了前向区域中存储分配决策的重要性。我们展示了所提出方法在现实案例公司中的有效性，且该方法可应用于具有不同仓库布局、订单规模和路径策略的其他场景。此外，该方法处理了补货和订单拣选顺序进行的常见情况。因此，位于其他国家并面临类似情况的电子商务配送中心也可采用此方法。

此情景建议o实施我们的方法，以加强其内部订单处理的生产效率 .

在大多数物流企业的实践中，提升订单拣选效率通常需要雇佣更多员工、购买更先进的设备或进行结构性改造，这会导致大量投资。然而，本研究提出的方法仅需对仓库管理系统中的存储分配程序进行轻微修改，从成本最小化的角度来看，易于采用。缩短行驶距离对拣选作业所需时间和运营成本具有显著影响。同时，不断扩张的电子商务市场要求配送中心在紧凑的时间窗口内快速及时地处理电子商务订单。快速配送能够提升客户体验，从而提供竞争优势。因此，为减少发货延迟，我们建议行业从业者采用快速且易于实施的方法，例如本文提出的方法。较短的运行时间适用于解决日常运营问题。我们相信，该方法在减少运行时间和延迟订单数量两方面的优势，使其对业界极具吸引力。

7. 结论和未来研究方向

本文研究了一种新型的储位分配问题，该问题是前向区域中出现的一种短期问题。新到达的物品需要存放在开放存储位置中，但部分存储位置最初已被其他物品占用。该分配决策旨在最小化订单拣选过程中给定订单的总行驶距离。我们首先将该问题建模为一个整数规划模型，并证明其为NP难问题。为了快速获得实用解，提出了一种两阶段分解算法。在阶段1中，采用不同的优先规则来选择开放存储位置；而在阶段2中，通过动态规划方法最优地求解货品分配问题。对于大规模实例，引入了束搜索启发式算法以加快求解时间。

我们将所提出的算法与文献中常见的随机存储、完全周转率存储、MDA和ARB等先前方法进行了比较。结果表明，我们的算法能够非常快速地找到近似最优解，并显著优于其他方法。建议管理者关注货品‐存储位置分配问题的最优解，因为我们的结果证明在此阶段可以获得改进。此外，结果还表明，忽略已存储物品的影响将导致性能劣于完全周转策略。因此，考虑部分位置被已存储物品占用这一约束条件至关重要。具体而言，在不同情况下，与不考虑该约束的分配问题相比，平均行驶距离减少了5%至13%。进一步地，首次针对已存储物品的影响，对三种路径策略（返回、S形和中点）进行了数学建模。我们研究了在何种情况下哪种路径策略最佳。

我们还在从中国第三方零售商收集的实际数据上测试了所提出的算法，结果表明，该解决方案显著优于公司当前使用的策略。

然而，本研究受到一些假设的限制，这些假设提示了对该工作的扩展方向。首先，考虑不确定性因素的影响来研究该算法将十分有意义，例如关于拣货订单的信息有限的情况。通过这种方式，可以将经常被同时需求的物品之间的关联性纳入基本模型中。此外，为该问题设计一个紧致的下界仍然是一个具有挑战性的任务。未来研究可以挑战我们的求解方法，并尝试提升其性能。

8. 资助

本研究得到国家自然科学基金委员会（NSFC）项目71991464/71991460、71871207、72071193、72091215/72091210、 71921001；中国顶尖青年人才计划；以及中央高校基本科研业务费专项资金的资助。