目录
一、线性表的类型定义
线性表是一种线性结构,是n(n≥0)个具有相同属性的数据元素所组成的有限序列
(a₁,a₂,...,aᵢ₋1,aᵢ,aᵢ₊1,...aₙ)
其中n为线性表中数据元素的个数(也为线性表的长度),当n=0时线性表为空表,当n>0时线性表为非空表
一个数据元素可以由多个数据项组成,数据元素可以是各种类型,但同一张线性表中的所有数据元素类型必须相同
线性表的抽象数据类型定义:
ADT List{
数据对象:D={aᵢ|aᵢ∈DataType, i=0, 1,..., n-1}
数据关系:R={<aᵢ,aᵢ₊1>|aᵢ,aᵢ₊1∈D}
基本操作:
ListInit(L):创建一个空线性表L
ListClear(L):清空线性表L中的数据元素
ListEmpty(L):判断线性表L是否为空表
ListLength(L):求线性表L中所含数据元素的个数(线性表的长度)
ListPrint(L):在线性表L不为空表时,按顺序依次输出线性表中的所有数据元素
ListInsert(L,i,x):插入数据元素(线性表L的第i个数据元素前插入数据元素x)
ListDelete(L,i,x):删除数据元素(删除线性表L的第i个数据元素,并将值通过x返回)
ListGet(L,i,x):按位查找(查询线性表L的第i个数据元素的值,并通过x返回)
ListLocate(L,x):按值查找(查询线性表L中第一个与x值相同的数据元素)
}ADT List
二、线性表的顺序存储结构及实现
顺序存储方式:在内存中用地址连续的有限的一块存储空间顺序存放各个元素
描述顺序结构:①存储空间的起始位置 ②顺序表的当前长度 ③顺序表的容量
优点:①不用为数据元素间的逻辑关系提供额外的存储空间 ②按位查找数据元素效率高
缺点:①执行插入和删除操作时效率低 ②静态存储方式导致存储空间会浪费或不够使用
线性表的顺序存储结构:
内存中的地址空间是线性的,若知道第一个元素的地址(基地址),则可知第i个元素的地址
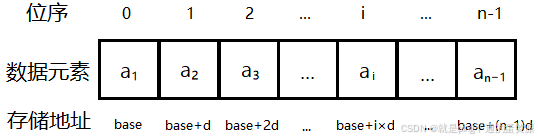
顺序存储结构的线性表的类型定义:
使用静态数组定义:
#define MAXSIZE 100 //定义顺序表的最大容量
typedef struct
{
DataType data[MAXSIZE]; //DataType为数据元素的数据类型,data为存放顺序表的数组名
int length; //顺序表的长度,length≤MAXSIZE
}SeqList; //顺序表的名称顺序表基本操作实现:
①初始化操作:算法的时间复杂度是O(1)
void ListInit(SeqList *L)
{
L->length=0; //构造一个空的顺序表,长度为0
}②清空操作
顺序表中变量退出作用域将自动释放变量存储单元
③判空操作:算法的时间复杂度是O(1)
bool ListEmpty(SeqList L)
{
if(L.length==0) //通过顺序表的长度判断表是否为空
return true; //返回布尔值
else
return false;
}④求表长操作:算法的时间复杂度是O(1)
int ListLength(SeqList L)
{
return L.length; //返回顺序表长度
}⑤遍历操作:算法的时间复杂度是O(n)
void ListPrint(SeqList L)
{
for(int i=0; i<L.length; i++) //依次输出顺序表中的数据元素
printf("%d", L.data[i]);
}⑥插入操作:算法的时间复杂度是O(n)
在顺序表的第i个位置上插入一个值为X的新数据元素
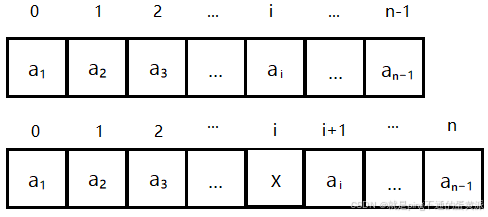
顺序表长由n变为n+1,i的取值范围为1 ≤ i ≤ n+1
当i=n+1时,直接在aₙ后插入新数据元素X
当1≤i≤n时,需要将aᵢ~aₙ的所有数据元素依次后移,为新的数据元素让出位置
bool ListInsert(SeqList *L, int i, DataType x)
{
int j;
if (L->length>=MAXSIZE) //检查顺序表是否已满
return false;
if(i<0 || i>L->length) //检查插入位置合法性
return false;
for(int j=L->length-1; j>=i; j--)
L->data[j+1]=L->data[j]; //第i个位置后的数组元素依次后移
L->data[i]=x; //新数据元素插入第i个位置
L->length++;//顺序表长度+1
return true;
}⑦删除操作:算法的时间复杂度是O(n)
将顺序表中第i个数据元素删除
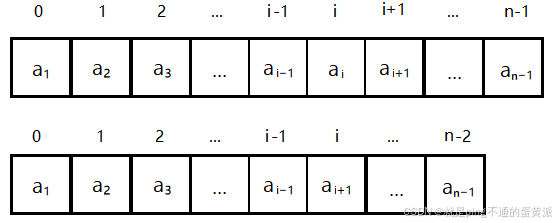
顺序表长由n变为n-1,i的取值范围为1 ≤ i ≤ n
当i<n时,删除数据元素aᵢ需要将aᵢ₊₁~aₙ的所有数据元素依次前移,并修改顺序表长L->length
bool ListDelete(SeqList *L, int i, DataType *x)
{
if(i<1 || i>L->length) //检查顺序表是否为空表和删除位置合法性
return false;
*x=L->data[i-1]; //取得被删除数据元素值
for(int j=i; j<=L->length-1; j++) //数据元素依次前移
L->data[j-1]=L->data[j];
L->length--; //顺序表长度-1
return true;
}⑧按位查找操作:算法的时间复杂度是O(1)
bool ListGet(SeqList L, int i, DataType *x)
{
if(i<1 || i>L.length) //检查顺序表是否为空表和删除位置合法性
return false;
else{
*x=L.data[i-1];
return true;
}
}⑨按值查找操作:算法的时间复杂度是O(n)
int ListLocate(SeqList L, DataType x)
{
int i=1;
while(i<=L.length && L.data[i-1]!=x) //遍历顺序表查找数据元素x
i++;
if(i<=L.length)
return i; //返回数据元素的位序
else
return 0; //查找失败
}将两张非递减有序的顺序表La和Lb合并得到一张新非递减有序的顺序表Lc
算法的时间复杂度是O(m+n)
void SeqListMerge(SeqList La, SeqList Lb, SeqList &Lc)
{
int m=La.length;int n=Lb.length;Lc.length=m+n;
int i,j,k; i=j=k=0; //初始化
while(i<m && j<n) //La和Lb均非空
if(La.data[i]<=Lb.data[j]) //La数据元素值≤Lb数据元素值
Lc.data[k++]=La.data[i++]; //La中的数据元素插入Lc
else
Lc.data[k++]=Lb.data[j++]; //Lb中的数据元素插入Lc
while(i<m)
Lc.data[k++]=La.data[i++]; //Lb已空,将La中所有剩余数据元素都插入Lc
while(j<n)
Lc.data[k++]=Lb.data[j++]; //La已空,将Lb中所有剩余数据元素都插入Lc
}顺序表基本操作的具体代码:
#include<stdio.h>
#include<iostream>
using namespace std;
//顺序表的数据元素类型设置为整数
typedef int DataType;
//顺序表存储结构
#define MAXSIZE 100
typedef struct
{
DataType data[MAXSIZE];
int length;
}SeqList;
//初始化空顺序表
void ListInit(SeqList *L)
{
L->length=0;
}
//判断顺序表是否为空表
bool ListEmpty(SeqList L)
{
if(L.length==0)
return true;
else
return false;
}
//求顺序表的长度
int ListLength(SeqList L)
{
return L.length;
}
//遍历顺序表
void ListPrint(SeqList L)
{
for(int i=0; i<L.length; i++)
printf("%d", L.data[i]);
}
//顺序表中插入新的数据元素
bool ListInsert(SeqList *L, int i, DataType x)
{
int j;
if (L->length>=MAXSIZE)
return false;
if(i<0 || i>L->length)
return false;
for(int j=L->length-1; j>=i; j--)
L->data[j+1]=L->data[j];
L->data[i]=x;
L->length++;
return true;
}
//删除顺序表中的数据元素
bool ListDelete(SeqList *L, int i, DataType *x)
{
if(i<1 || i>L->length)
return false;
*x=L->data[i-1];
for(int j=i; j<=L->length-1; j++)
L->data[j-1]=L->data[j];
L->length--;
return true;
}
//按位查找顺序表中数据元素
bool ListGet(SeqList L, int i, DataType *x)
{
if(i<1 || i>L.length)
return false;
else{
*x=L.data[i-1];
return true;
}
}
//按值查找顺序表中数据元素
int ListLocate(SeqList L, DataType x)
{
int i=1;
while(i<=L.length && L.data[i-1]!=x)
i++;
if(i<=L.length)
return i;
else
return 0;
}
//将两张非递减有序的顺序表La和Lb合并得到一张新非递减有序的顺序表Lc
void SeqListMerge(SeqList La, SeqList Lb, SeqList &Lc)
{
int m=La.length;int n=Lb.length;Lc.length=m+n;
int i,j,k; i=j=k=0;
while(i<m && j<n)
if(La.data[i]<=Lb.data[j])
Lc.data[k++]=La.data[i++];
else
Lc.data[k++]=Lb.data[j++];
while(i<m)
Lc.data[k++]=La.data[i++];
while(j<n)
Lc.data[k++]=Lb.data[j++];
}
int main(){
SeqList La; //定义一个顺序表La
ListInit(&La); //初始化顺序表La
cout<<"判断顺序表La是否为空表(1为空表,0为非空表):"<<ListEmpty(La)<<endl;
ListInsert(&La,0,1); //在顺序表La中插入数据元素 1
ListInsert(&La,1,3); //在顺序表La中插入数据元素 3
ListInsert(&La,2,5); //在顺序表La中插入数据元素 5
cout<<"插入数据元素后判断顺序表La是否为空表(1为空表,0为非空表):"<<ListEmpty(La)<<endl;
cout<<"顺序表La中所含数据元素的个数:"<<ListLength(La)<<endl;
cout<<"输出顺序表La中所有的数据元素:"; ListPrint(La);
int x; ListGet(La,1,&x); cout<<endl<<"查询顺序表La的第一个数据元素的值:"<<x<<endl;
cout<<"查询顺序表La中第一个与值为3的数据元素的位置:"<<ListLocate(La,3)<<endl;
int y; ListDelete(&La,3,&y); cout<<"删除顺序表La中的第三个数据元素,被删除数据元素的值:"<<y<<endl;
SeqList Lb;
ListInit(&Lb);
ListInsert(&Lb,0,1); ListInsert(&Lb,1,2); ListInsert(&Lb,2,3); ListInsert(&Lb,3,4);
SeqList Lc;
ListInit(&Lc);
cout<<"输出顺序表La中所有的数据元素:"; ListPrint(La); cout<<endl;
cout<<"输出顺序表Lb中所有的数据元素:"; ListPrint(Lb); cout<<endl;
SeqListMerge(La,Lb,Lc);
cout<<"输出顺序表Lc中所有的数据元素:"; ListPrint(Lc);
return 0;
}三、线性表的链式存储结构及实现
链式存储方式:数据元素用任意的存储单元来存储,逻辑相邻的两个数据元素的存储空间可以连续,也可以不连续
优点:①执行插入和删除操作时效率高 ②动态分配存储空间
缺点:①存储密度不高 ②执行查询操作时效率低
常用的链式存储结构包括:单链表、循环链表和双向链表
线性表的链式存储结构:
指针变量L存放第一个结点的地址,标志线性链表开始
最后一个结点没有后继,指针域为NULL,标志链表结束
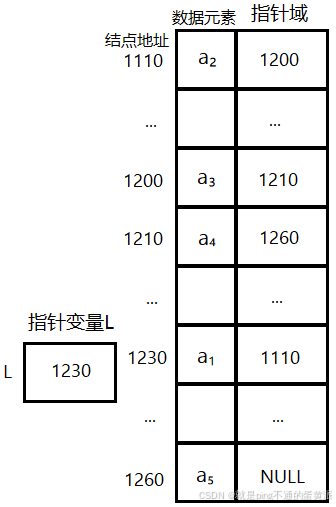
链式存储结构的线性表的类型定义:
typedef struct LNode
{
DataType data; //存储数据元素
struct LNode *next; //指向后继结点的地址
}LNode, *LinkedList; //LNode是结点的类型,LinkedList是指向LNode类型结点的指针类型单链表(线性链表(Linear Linked List))的每个数据元素被称为“结点”,每个结点中只有一个指向后继的指针
每个结点至少包括数据域(data存储数据元素信息)和指针域(next存储直接后继的存储位置)

线性链表的逻辑表示:

带头结点的单链表:
为了运算方便,在线性链表的第一个结点之前加入一个结点(头结点)
①空单链表:

②非空单链表:
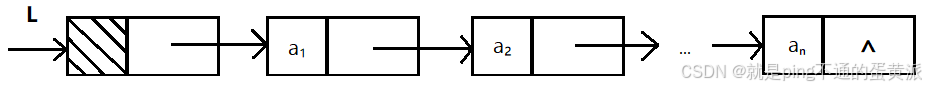
单链表基本操作实现:
采用动态存储表示时,链表结点的存储空间需要在运行中根据需要申请
利用C的内存分配函数malloc()完成,需要包含标准库头文件<stdlib.h>
p = (LNode*)malloc(sizeof(LNode));
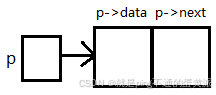
①申请一块LNode类型的存储单元
②将这块存储单元的首地址赋值给变量p
回收内存函数free()能够删除结点
①初始化操作
void ListInit(LinkedList *L)
{
*L=(LNode*)malloc(sizeof(LNode)); //申请空间
(*L)->next=NULL; //置指针域为空指针标识链表结束
}使用尾插法建立单链表
读入的数据元素的顺序与生成的链表中的数据元素的顺序相同
LinkedList CreatTail(LinkedList &L, DataType a[], int n)
{
LNode *p, *r;
int i;
L = (LNode *)malloc(sizeof(LNode)); //申请头结点
r = L; //初始化,尾指针指向头结点
for (i = 0; i < n; i++) //n为要建立的单链表数据元素个数
{
p = (LNode *)malloc(sizeof(LNode)); //申请新结点
p->data = a[i]; //结点数据域赋值
r->next = p; //在尾部插入新结点
r = p; //r指向新的尾结点
}
r->next = NULL;
return L;
}使用头插法建立单链表
读入的数据元素的顺序与生成的链表中的数据元素的顺序相反
LinkedList CreatHead(LinkedList &L,DataType a[], int n)
{
L=(LNode *)malloc(sizeof(LNode)); //申请头结点
L->next=NULL; //初始化一个空链表,L为头指针
for(int i=0;i<n;i++)
{
LNode *p=(LNode *)malloc(sizeof(LNode)); //申请新的结点
p->data=a[i]; //结点数据域赋值
p->next=L->next; L->next=p; //插入表头
}
return L;
}②清空操作:算法的时间复杂度是O(n)
void ListClear(LinkedList L)
{
LNode *p=L->next,*q; //p指向第一个结点
while(p!=NULL)
{
q=p->next; //记住后继结点
free(p); //释放p结点
p=q; //移至待处理结点
}
L->next=NULL; //置表尾为空
}③判空操作:算法的时间复杂度是O(1)
bool ListEmpty(LinkedList L)
{
if(L->next==NULL) //通过头结点的指针域判断单链表是否为空
return true;
else
return false;
}④求表长操作:算法的时间复杂度是O(n)
int ListLength(LinkedList L)
{
LinkedList p=L->next; //p指向第一个数据元素结点
int len=0; //计数器初始化
while(p)
{
len++;
p=p->next; //计数器+1,指针p后移
}
return len;
}⑤遍历操作:算法的时间复杂度是O(n)
void ListPrint(LinkedList L)
{
LNode *p = L->next;
while (p != NULL)
{
printf("%d", p->data); //输出结点的值
p = p->next; //指针p后移
}
}⑥插入操作:算法的时间复杂度是O(n)
因为单链表带头结点,在表头、表中、表尾插入数据元素的操作语句相同
在单链表中的第i个结点之前插入一个结点*s
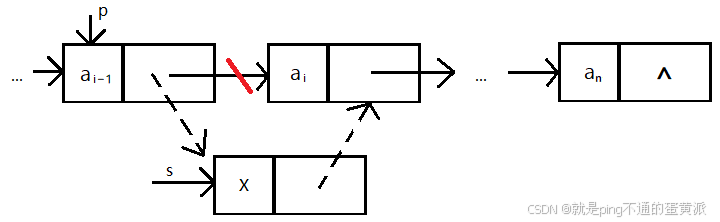
先找到第i-1个结点,改变指针之间的逻辑关系
s指向指针p的后继结点(第i个结点)
然后将s的值存入结点*p的next域中
bool ListInsert(LinkedList L, int i, DataType x)
{
LinkedList p, s;
int count;
p = L;
count = 0; //初始化计数器
if (p == NULL){
printf("p为空 ");exit(0);
}
while (p != NULL && count < i - 1){ //查找第i-1个结点
p = p->next;count++;
}
if (p == NULL)
return false;
else{
s = (LNode *)malloc(sizeof(LNode));
s->data = x;s->next = p->next;p->next = s; //将结点s插入结点p之后
return true;
}
}⑦删除操作:算法的时间复杂度是O(n)
将单链表中第i个结点删除

找到*q的前驱结点*p,改变指针之间的逻辑关系
bool ListDelete(LinkedList L, int i, DataType *x)
{
LNode *pre = L,*p; int count = 0;
while (pre != NULL && count < i - 1) //查找第i-1个结点
{
pre = pre->next;
count++;
}
if (pre == NULL || pre->next == NULL) //若参数不合法
return false;
else
{
p = pre->next; *x = p->data; //存储被删数据元素值
pre->next = p->next; //修改指针指向
free(p); //释放被删数据元素空间
return true;
}
}⑧按位查找操作:算法的时间复杂度是O(n)
bool ListGet(LinkedList L, int i, DataType *x) //DataType *x存放查找的值
{
if (i < 1)
return false;
LNode *p = L->next; //p指向第一元素结点
int j = 1; //计数器初始化
while (p != NULL && j < i) //后移指针
{
p = p->next; j++;
}
if (p != NULL)
{
*x = p->data; //查找成功
return true;
}
else
return false; //查找失败
}⑨按值查找操作:算法的时间复杂度是O(n)
int ListLocate(LinkedList L, DataType x) //DataType x存放查找数据元素的值
{
LNode *p = L->next; //p指向第一个结点
int j = 1; //计数器初始化
while (p != NULL && p->data != x)
{
p = p->next; j++;
}
if (p!=NULL && p->data == x)
return j; //查找成功,返回数据元素的位序
else
return 0; //查找失败
}将两张非递减有序的单链表La和Lb合并得到一张新非递减有序的单链表Lc
算法的时间复杂度是O(m+n)
LinkedList Union(LinkedList La, LinkedList Lb)
{
LNode *Lc, *pa, *pb, *pc;
Lc = (LNode *)malloc(sizeof(LNode)); //申请结点
Lc->next = NULL; //初始化链表Lc
pa = La->next; //pa是链表La的工作指针
pb = Lb->next; //pb是链表Lb的工作指针
pc = Lc; //pc是链表Lc的工作指针
while (pa && pb) //La和Lb均非空
if (pa->data <= pb->data)
{
pc->next = pa; //La中元素插入Lc
pc = pa;
pa = pa->next;
}
else
{
pc->next = pb; //Lb中元素插入Lc
pc = pb;
pb = pb->next;
}
if (pa)
pc->next = pa; //若pa未结束,将pc指向pa
else
pc->next = pb; //若pb未结束,将pc指向pb
return Lc;
}单链表基本操作的具体代码:
#include<stdlib.h>
#include<cstdio>
#include<iostream>
using namespace std;
//单链表的数据元素类型设置为整数
typedef int DataType;
//单链表存储结构
typedef struct LNode
{
DataType data;
struct LNode *next;
}LNode, *LinkedList;
//初始化空单链表
void ListInit(LinkedList *L)
{
*L=(LNode*)malloc(sizeof(LNode));
(*L)->next=NULL;
}
//尾插法建立单链表
LinkedList CreatTail(LinkedList &L, DataType a[], int n)
{
LNode *p, *r;
int i;
L = (LNode *)malloc(sizeof(LNode));
r = L;
for (i = 0; i < n; i++)
{
p = (LNode *)malloc(sizeof(LNode));
p->data = a[i];
r->next = p;
r = p;
}
r->next = NULL;
return L;
}
//头插法建立单链表
LinkedList CreatHead(LinkedList &L,DataType a[], int n)
{
L=(LNode *)malloc(sizeof(LNode));
L->next=NULL;
for(int i=0;i<n;i++)
{
LNode *p=(LNode *)malloc(sizeof(LNode));
p->data=a[i];
p->next=L->next; L->next=p;
}
return L;
}
//清空单链表中的所有数据元素
void ListClear(LinkedList L)
{
LNode *p=L->next,*q;
while(p!=NULL)
{
q=p->next;
free(p);
p=q;
}
L->next=NULL;
}
//判断单链表是否为空表
bool ListEmpty(LinkedList L)
{
if(L->next==NULL)
return true;
else
return false;
}
//求单链表的长度
int ListLength(LinkedList L)
{
LinkedList p=L->next;
int len=0;
while(p)
{
len++;
p=p->next;
}
return len;
}
//遍历单链表
void ListPrint(LinkedList L)
{
LNode *p = L->next;
while (p != NULL)
{
printf("%d", p->data);
p = p->next;
}
}
//单链表中插入新的数据元素
bool ListInsert(LinkedList L, int i, DataType x)
{
LinkedList p, s;int count;p = L;count = 0;
if (p == NULL){
printf("p为空 ");exit(0);
}
while (p != NULL && count < i - 1){
p = p->next;count++;
}
if (p == NULL)
return false;
else{
s = (LNode *)malloc(sizeof(LNode));
s->data = x;s->next = p->next;p->next = s;
return true;
}
}
//删除单链表中的数据元素
bool ListDelete(LinkedList L, int i, DataType *x)
{
LNode *pre = L,*p; int count = 0;
while (pre != NULL && count < i - 1)
{
pre = pre->next; count++;
}
if (pre == NULL || pre->next == NULL)
return false;
else
{
p = pre->next; *x = p->data;
pre->next = p->next;
free(p);
return true;
}
}
//按位查找单链表中的数据元素
bool ListGet(LinkedList L, int i, DataType *x)
{
if (i < 1)
return false;
LNode *p = L->next;
int j = 1;
while (p != NULL && j < i)
{
p = p->next; j++;
}
if (p != NULL)
{
*x = p->data;
return true;
}
else
return false;
}
//按值查找单链表中的数据元素
int ListLocate(LinkedList L, DataType x)
{
LNode *p = L->next;
int j = 1;
while (p != NULL && p->data != x)
{
p = p->next; j++;
}
if (p!=NULL && p->data == x)
return j;
else
return 0;
}
//将两张非递减有序的单链表La和Lb合并得到一张新非递减有序的单链表Lc
LinkedList Union(LinkedList La, LinkedList Lb)
{
LNode *Lc, *pa, *pb, *pc;
Lc = (LNode *)malloc(sizeof(LNode));
Lc->next = NULL;
pa = La->next;
pb = Lb->next;
pc = Lc;
while (pa && pb)
if (pa->data <= pb->data)
{
pc->next = pa;
pc = pa;
pa = pa->next;
}
else
{
pc->next = pb;
pc = pb;
pb = pb->next;
}
if (pa)
pc->next = pa;
else
pc->next = pb;
return Lc;
}
int main()
{
LinkedList La; //定义一个单链表La
ListInit(&La); //初始化单链表La
cout<<"判断单链表La是否为空表(1为空表,0为非空表):"<<ListEmpty(La)<<endl;
DataType a[3]={1,3,5};
CreatTail(La,a,3);//使用尾插法建立单链表La
cout<<"判断单链表La是否为空表(1为空表,0为非空表):"<<ListEmpty(La)<<endl;
cout<<"单链表La中所含数据元素的个数:"<<ListLength(La)<<endl;
int x; ListGet(La,1,&x); cout<<"查询单链表La的第一个数据元素的值:"<<x<<endl;
cout<<"查询单链表La中第一个与值为3的数据元素的位置:"<<ListLocate(La,3)<<endl;
int y; ListDelete(La,3,&y); cout<<"删除单链表La中的第三个数据元素,被删除数据元素的值:"<<y<<endl;
cout<<"在单链表La中的第三个位置上插入数据元素5"<<endl;ListInsert(La,3,5);
LinkedList Lb; //定义一个单链表Lb
ListInit(&Lb); //初始化单链表Lb
DataType b[3]={4,3,2};
CreatHead(Lb,b,3);//使用头插法建立单链表Lb
cout<<"判断单链表Lb是否为空表(1为空表,0为非空表):"<<ListEmpty(Lb)<<endl;
cout<<"输出单链表La中所有的数据元素:"; ListPrint(La); cout<<endl;
cout<<"输出单链表Lb中所有的数据元素:"; ListPrint(Lb); cout<<endl;
LinkedList Lc=Union(La,Lb);
cout<<"输出单链表Lc中所有的数据元素:"; ListPrint(Lc); cout<<endl;
cout<<"清空单链表Lc中所有的数据元素";ListClear(Lc); cout<<endl;
cout<<"判断单链表Lc是否为空表(1为空表,0为非空表)"<<ListEmpty(Lc)<<endl;
return 0;
}




















 1119
1119

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








