回溯法例题

晚睡贵妃写代码

于 2024-12-22 18:58:05 发布

阅读量945

点赞数 29

分类专栏：基础算法文章标签：算法 java 学习

本文链接：https://blog.youkuaiyun.com/m0_75039094/article/details/144595388

版权

基础算法专栏收录该内容

9 篇文章

订阅专栏

例一:0-1背包问题

https://ac.nowcoder.com/acm/problem/226514

这个题的解空间是子集树，大家可以自己来画一下。

算法思想

定义问题参数：首先定义了物品的数量n，背包的容量c，以及两个数组w和v分别存储每个物品的重量和价值。
初始化变量：初始化了用于记录当前选择的物品总重量sumweight和总价值sumvalue，以及用于记录最优解的变量opvalue和fullvalue，还有记录最优解选择的数组op。
深度优先搜索（DFS）：使用深度优先搜索（DFS）算法来探索所有可能的物品组合。dfs方法是一个递归函数，它尝试将每个物品放入或不放入背包，并递归地处理剩余的物品。
选择与回溯：在dfs方法中，对于每个物品i，算法尝试两种选择：（1）不放入背包（x[i] = 0），然后递归处理下一个物品（dfs(i+1)）。（2）放入背包（x[i] = 1），但前提是放入后背包的总重量不超过背包容量c。如果放入后总重量不超过容量，更新当前的总重量和总价值，然后递归处理下一个物品。递归返回后，撤销这次选择（回溯），恢复sumweight和sumvalue的状态。
更新最优解：在递归过程中，如果当前选择的物品组合的总价值sumvalue超过了之前记录的最优价值opvalue，或者当背包恰好装满时，如果当前价值超过了fullvalue，则更新最优解。
输出结果：main方法中，首先读取输入，然后调用dfs方法从第一个物品开始搜索。搜索完成后，输出记录的最优价值opvalue和背包恰好装满时的最优价值fullvalue。

时间复杂度分析

基本操作：对于每个物品，都有放入背包和不放入背包两种选择。因此，对于n个物品，总共有 $2^{n}$ 种可能的组合。
递归树：在回溯算法中，每个物品都对应递归树的一层，每层有两个分支（放入或不放入背包）。因此，递归树的深度为n，每层有2个分支，总共有 $2^{n}$ 个叶子节点。
计算每个叶子节点：到达每个叶子节点的过程中，需要进行比较和更新操作，这些操作的时间复杂度为O(1)。因此，计算每个叶子节点的时间复杂度为O(1)。
总时间复杂度：由于有 $2^{n}$ 个叶子节点，每个叶子节点的计算时间为O(1)，因此总的时间复杂度为O( $2^{n}$ )。

但是这个题非常尴尬，只有百分之六十的可以在2s内完成，并不能完全通过。但是我们还是需要掌握种方法，可能还有优化的方法，但是此处就不再继续介绍了。

总结

这段代码通过回溯算法解决了0/1背包问题，其时间复杂度为O( $2^{n}$ )，空间复杂度为O(n)。这种算法适用于物品数量较少的情况，因为当物品数量增加时，计算量会呈指数级增长，导致算法效率降低。对于大规模的0/1背包问题，可能需要考虑使用动态规划或其他更高效的算法。

伪代码

类 Main:
    常量 N = 100000 // 默认物品数量
    数组 w[N] // 物品重量或体积
    数组 v[N] // 物品价值
    数组 x[N] // 是否放入背包，1为放入，0为不放
    变量 n, c // 物品总数，背包最大容量
    变量 sumweight = 0 // 当前放入物品的总重量或总体积
    变量 sumvalue = 0 // 当前放入背包的总价值

    变量 opvalue = 0 // 最优价值
    变量 fullvalue = 0 // 背包恰好装满时的最优价值
    数组 op[N] // 最优解

    方法 dfs(t):
        如果 t > n:
            如果 sumvalue > opvalue:
                opvalue = sumvalue
                对于 i 从 1 到 n:
                    op[i] = x[i]
            如果 sumweight == c 且 sumvalue > fullvalue:
                fullvalue = sumvalue
        否则:
            x[t] = 0
            dfs(t + 1)
            x[t] = 1
            如果 sumweight + w[t] <= c:
                sumweight += w[t]
                sumvalue += v[t]
                dfs(t + 1)
                sumweight -= w[t]
                sumvalue -= v[t]

    方法 main:
        创建 Scanner对象 scanner 用于读取输入
        读取 n 和 c
        对于 i 从 1 到 n:
            读取 w[i] 和 v[i]
        dfs(1)
        打印 opvalue
        打印 fullvalue

java实现代码

import java.util.Scanner;

public class Main{
    static final int N=100000;//默认有多少个物品
    static int[] w=new int[N];//每个物品的重量或体积
    static int[] v=new int[N];//每个物品的价值
    static int[] x=new int[N];//判断是否放入背包，为1则放入，为0则不放
    static int n,c;//一共有n个物品，背包最大容量c
    static int sumweight=0;//目前放入的物品的总重量或总体积
    static int sumvalue=0;//目前放入背包的总价值
    
    static int opvalue=0;//最优价值
    static int fullvalue=0;//当背包恰好装满时的最优价值
    static int[] op=new int[N];//最优解
    
    //回溯，表示在第i层,从1开始
    public static void dfs(int t){
        if(t>n){
            if(sumvalue>opvalue){
                opvalue=sumvalue;
                for(int i=1;i<=n;i++){
                    op[i]=x[i];
                }
            }
            if(sumweight==c&&sumvalue>fullvalue){
                //如果背包恰好装满且比之前的full大，则更新
                fullvalue=sumvalue;
            }
        }
        else{
            //当没有到达叶子结点时，继续向下搜索
            x[t]=0;
            dfs(t+1);
            x[t]=1;
            if(sumweight+w[t]<=c){
                sumweight+=w[t];
                sumvalue+=v[t];
                dfs(t+1);
                sumweight-=w[t];
                sumvalue-=v[t];
            }
        }
    }
    public static void main(String[] args){
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        c=scanner.nextInt();
        for(int i=1;i<=n;i++){
            w[i]=scanner.nextInt();
            v[i]=scanner.nextInt();
        }
        dfs(1);
        System.out.println(opvalue);
        System.out.println(fullvalue);
    }
}

例二：加工生产调度（牛客）

https://ac.nowcoder.com/acm/problem/50164

算法思想

目标：从n个产品的所有排列中找出具有最小完成时间和的调度方案。

（1）批处理调度问题的解空间是一颗排列树。

（2）回溯法搜索排列树。

定义问题参数：定义了作业数量n，两台机器上各作业的处理时间矩阵m，以及两个数组x和bestx来分别存储当前和最优的作业调度顺序。

初始化变量：初始化了变量f1和f2来记录两台机器的完成处理时间，cf来记录完成所有作业的总时间，以及bestf来存储当前找到的最优处理时间。

回溯算法：backtrack方法是一个递归函数，它尝试所有可能的作业执行顺序。对于每个作业，算法有两个选择：

将作业j安排在当前位置t，并递归地处理下一个作业。
不将作业j安排在当前位置，继续处理下一个可能的作业。

剪枝：在递归过程中，如果当前的总完成时间cf已经超过了已知的最优时间bestf，则停止进一步的递归（剪枝），以减少不必要的计算。

更新最优解：如果找到一个更优的作业调度顺序，即总完成时间cf小于当前最优时间bestf，则更新bestf和最优作业调度顺序bestx。

输出结果：在main方法中，首先读取输入，然后调用backtrack方法从第一个作业开始搜索。搜索完成后，输出最优的作业调度顺序和处理时间。

时间复杂度分析

由于是采用了排列树解空间，时间复杂度为O(n!)。这段代码的时间复杂度是指数级的，具体为O(n!)，其中n是作业的数量。这是因为算法使用回溯法来探索所有可能的作业调度顺序。对于每个作业，算法都尝试将其放在当前位置或跳过，因此搜索树有n!个叶子节点，每个叶子节点对应一种作业调度顺序。

伪代码

类 test:
    属性 x[100] // 当前作业调度数组
    属性 bestx[100] // 最优作业调度数组
    属性 m[100][100] // 各作业在各机器上的处理时间
    属性 f1 // 机器1完成处理时间
    属性 f2 // 机器2完成处理时间
    属性 cf // 所有作业完成处理时间的和
    属性 bestf // 最优处理时间
    属性 n // 作业数

    方法 swap(arr, a, b):
        临时变量 temp = arr[a]
        arr[a] = arr[b]
        arr[b] = temp

    方法 backtrack(t):
        如果 t > n:
            如果 cf < bestf:
                对于 i 从 1 到 n:
                    bestx[i] = x[i] // 更新最优调度序列
                bestf = cf // 更新最优目标值
        否则:
            对于 j 从 t 到 n:
                f1 += m[x[j]][1] // 机器1上执行第x[j]个任务
                tempf = f2
                f2 = max(f1, f2) + m[x[j]][2] // 机器2上执行第x[j]个任务
                cf += f2
                如果 cf < bestf:
                    swap(x, t, j) // 交换任务位置
                    backtrack(t + 1) // 递归搜索下一层
                    swap(x, t, j) // 回溯
                f1 -= m[x[j]][1]
                cf -= f2
                f2 = tempf

    方法 main:
        创建 test类实例 jobScheduling
        创建 Scanner对象 scanner 用于读取输入
        打印 "请输入作业数："
        读取 jobScheduling.n
        打印 "请输入在各机器上的处理时间"
        对于 i 从 1 到 2:
            对于 j 从 1 到 jobScheduling.n:
                读取 jobScheduling.m[j][i]
        对于 i 从 1 到 jobScheduling.n:
            jobScheduling.x[i] = i // 初始化作业调度
        jobScheduling.backtrack(1) // 开始回溯搜索

        打印 "调度作业顺序："
        对于 i 从 1 到 jobScheduling.n:
            打印 jobScheduling.bestx[i] + " "
        打印 ""

        打印 "处理时间："
        打印 jobScheduling.bestf

java实现代码

import java.util.Scanner;

public class test {
        int[] x = new int[100]; // 当前作业调度
        int[] bestx = new int[100]; // 当前最优作业调度
        int[][] m = new int[100][100]; // 各作业所需的处理时间
        int f1 = 0; // 机器1完成处理时间
        int f2 = 0; // 机器2完成处理时间
        int cf = 0; // 完成时间和
        int bestf = 10000; // 当前最优值，即最优的处理时间和
        int n; // 作业数

        public void swap(int[] arr, int a, int b) {
            int temp = arr[a];
            arr[a] = arr[b];
            arr[b] = temp;
        }

        public void backtrack(int t) {
            if (t > n) { // 到达叶子结点，搜索到最底部
                if (cf < bestf) {
                    for (int i = 1; i <= n; i++) {
                        bestx[i] = x[i]; // 更新最优调度序列
                    }
                    bestf = cf; // 更新最优目标值
                }
            } else { // 非叶子结点
                for (int j = t; j <= n; j++) {
                    f1 += m[x[j]][1]; // 选择第x[j]个任务在机器1上执行
                    int tempf = f2;
                    f2 = Math.max(f1, f2) + m[x[j]][2]; // 保存当前作业在机器2的完成时间
                    cf += f2; // 在机器2上的完成时间和
                    if (cf < bestf) { // 总时间小于最优时间
                        swap(x, t, j); // 交换两个作业的位置
                        backtrack(t + 1); // 深度搜索解空间树，进入下一层
                        swap(x, t, j); // 回溯，还原
                    }
                    // 回溯需要还原各个值
                    f1 -= m[x[j]][1];
                    cf -= f2;
                    f2 = tempf;
                }
            }
        }

        public static void main(String[] args) {
            test jobScheduling = new test();
            Scanner scanner = new Scanner(System.in);

            System.out.println("请输入作业数：");
            jobScheduling.n = scanner.nextInt();

            System.out.println("请输入在各机器上的处理时间");
            for (int i = 1; i <= 2; i++) {
                for (int j = 1; j <= jobScheduling.n; j++) {
                    jobScheduling.m[j][i] = scanner.nextInt(); // 第j个作业，第i台机器的时间值
                }
            }
            for (int i = 1; i <= jobScheduling.n; i++) {
                jobScheduling.x[i] = i; // 初始化当前作业调度的一种排列顺序
            }
            jobScheduling.backtrack(1);

            System.out.println("调度作业顺序：");
            for (int i = 1; i <= jobScheduling.n; i++) {
                System.out.print(jobScheduling.bestx[i] + " ");
            }
            System.out.println();

            System.out.println("处理时间：");
            System.out.println(jobScheduling.bestf);
        }
    }

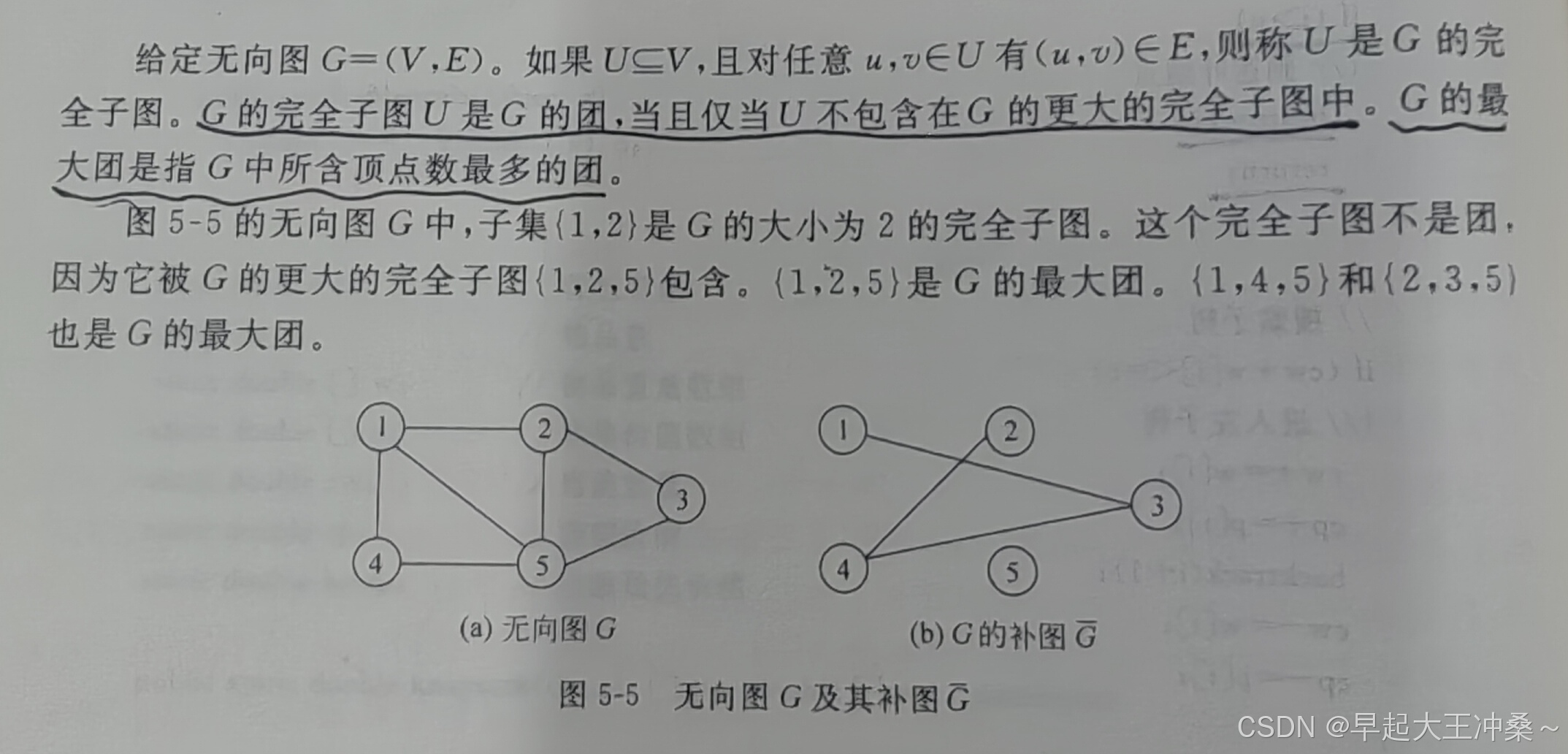
例三：最大团问题

算法思想

初始化：首先初始化邻接矩阵m，表示图中顶点之间的连接关系。

输入图信息：读取图的顶点数和边数，然后根据输入的边信息填充邻接矩阵。

回溯搜索：getbestn方法是一个递归函数，用于探索所有可能的顶点组合，以找到最大的团。对于每个顶点，算法尝试将其加入当前团（x[i] = 1），然后递归地处理下一个顶点。如果当前顶点与团中已有的顶点不相邻（m[i][j] == 0），则不将其加入团（x[i] = 0）。

剪枝：在递归过程中，如果当前团的大小加上剩余顶点数小于已知的最大团大小，则停止进一步的递归，以减少不必要的计算。

更新最优解：如果找到一个更大的团，更新最优解bestn和最优解数组bestx。

输出结果：最后，输出最大团的大小和包含的顶点。

时间复杂度

这段代码的时间复杂度是指数级的，具体为O(n^(n/2))，其中n是顶点的数量。这是因为在最坏的情况下，算法需要探索所有可能的顶点组合。由于最大团问题是一个NP完全问题，目前没有已知的多项式时间算法能够解决所有情况。然而，通过剪枝策略，算法可以避免一些不必要的计算，从而在一定程度上提高效率。对于较小的图，这种回溯算法是可行的，但对于大型图，可能需要更高效的算法或启发式方法。

伪代码

类 test:
    属性 m[101][101] // 有向图的邻接矩阵
    属性 x[101] // 当前团的解
    属性 bestx[101] // 最优解
    属性 n // 图的顶点数
    属性 cn // 当前团的大小
    属性 bestn // 当前最优值

    方法 getbestn(i):
        如果 i > n:
            bestn = cn
            对于 j 从 1 到 n:
                bestx[j] = x[j]
            返回
        x[i] = 1
        对于 j 从 1 到 i-1:
            如果 x[j] == 1 且 m[i][j] == 0:
                x[i] = 0
                中断循环
        如果 x[i] == 1:
            cn++
            调用 getbestn(i + 1)
            cn--
        x[i] = 0
        如果 cn + n - i > bestn:
            调用 getbestn(i + 1)

    方法 main:
        创建 test类实例 maxClique
        创建 Scanner对象 scanner 用于读取输入
        打印 "请输入图的顶点数："
        读取 maxClique.n
        打印 "请输入边的条数："
        读取边的数量 m
        对于 i 从 1 到 maxClique.n:
            对于 j 从 1 到 maxClique.n:
                maxClique.m[i][j] = 0
        当 m != 0:
            m--
            读取边的起点 i 和终点 j
            maxClique.m[i][j] = 1
            maxClique.m[j][i] = 1

        调用 maxClique.getbestn(1)
        打印 "最大团的大小为：" + maxClique.bestn

        打印 "最大团的顶点为："
        对于 i 从 1 到 maxClique.n:
            如果 maxClique.bestx[i] == 1:
                打印 i + " "
        打印空行

java实现代码

import java.util.Scanner;

public class test {
    int[][] m = new int[101][101]; // 有向图的邻接矩阵
    int[] x = new int[101]; // 当前团的解
    int[] bestx = new int[101]; // 最优解
    int n; // 表示图的顶点数
    int cn = 0; // 当前团的大小
    int bestn; // 当前最优值

    void getbestn(int i) {
        if (i > n) { // 递归出口，到根节点时，更新最优值和最优解，返回
            bestn = cn; // 更新最优值
            for (int j = 1; j <= n; j++) {
                bestx[j] = x[j];
            }
            return; // 返回
        }
        x[i] = 1; // 先假定x[i] = 1;
        for (int j = 1; j < i; j++) {
            if (x[j] == 1 && m[i][j] == 0) {
                x[i] = 0; // 如果该点与已知解中的点无边相邻
                break; // 则不遍历左子树
            }
        }
        if (x[i] == 1) { // 当且仅当x[i] == 1时，遍历左子树
            cn++; // 该点加入当前解
            getbestn(i + 1); // 递归调用
            cn--; // 还原当前解
        }
        x[i] = 0; // 假定x[i] = 0
        if (cn + n - i > bestn) { // 如果当前值+右子树可能选择的节点 < 当前最优解，不遍历左子树
            x[i] = 0;
            getbestn(i + 1);
        }
    }

    public static void main(String[] args) {
        test maxClique = new test();
        Scanner scanner = new Scanner(System.in);

        System.out.println("请输入图的顶点数：");
        maxClique.n = scanner.nextInt(); // 输入图的顶点数
        System.out.println("请输入边的条数：");
        int m = scanner.nextInt(); // 输入边的条数
        System.out.println("请输入图的邻接矩阵：");
        for (int i = 1; i <= maxClique.n; i++) {
            for (int j = 1; j <= maxClique.n; j++) {
                //初始化
                maxClique.m[i][j]=0;
                //maxClique.m[i][j] = scanner.nextInt(); // 输入图的邻接矩阵
            }
        }
        while(m!=0){
            m--;
            int i=scanner.nextInt();
            int j=scanner.nextInt();
            maxClique.m[i][j]=1;
            maxClique.m[j][i]=1;
        }


        // 求最优解
        maxClique.getbestn(1);
        System.out.println("最大团的大小为：" + maxClique.bestn); // 输出最优值

        // 输出最优解
        System.out.print("最大团的顶点为：");
        for (int i = 1; i <= maxClique.n; i++) {
            if (maxClique.bestx[i] == 1) {
                System.out.print(i + " ");
            }
        }
        System.out.println();
    }
}

例四：装载问题

构造子集树：

算法思想

定义问题参数：定义了背包的最大容量V，物品数量n，以及一个数组v来存储每个物品的体积。
初始化变量：初始化了一个变量sumv来记录遍历过程中找到的最大体积和，以及一个变量left来表示在递归过程中背包的剩余容量。
深度优先搜索（DFS）：dfs方法是一个递归函数，它尝试将每个物品放入或不放入背包，并递归地处理剩余的物品。对于每个物品，算法有两个选择：
放入背包：如果放入当前物品后背包的剩余容量仍然非负，那么将该物品的体积加到left上，然后递归地处理下一个物品。
不放入背包：直接递归地处理下一个物品。
更新最优解：在递归的每一步，如果当前的left（即背包剩余容量）大于sumv，则更新sumv为left的值。这样，当遍历完所有物品后，sumv将存储最大的未被选择的物品体积之和。
输出结果：在main方法中，首先读取输入，然后调用dfs方法从第一个物品开始搜索。搜索完成后，输出V - sumv，即背包容量减去最大未被选择的物品体积之和，这就是可以放入背包的物品的最大体积。

时间复杂度分析

这段代码的时间复杂度是指数级的，具体为O(2^n)，其中n是物品的数量。这是因为算法使用深度优先搜索来探索所有可能的物品组合。对于每个物品，算法都有两种选择（放入或不放入背包），因此搜索树有2^n个叶子节点，每个叶子节点对应一种物品组合。

伪代码

类 Main:
    常量 N = 30
    变量 n // 物品数量
    变量 V // 背包容量
    数组 v[N] // 每个物品的体积
    变量 sumv = 0 // 当前选择的物品总体积
    变量 left = 0 // 背包剩余容量

    方法 dfs(t):
        如果 t >= n:
            如果 left > sumv:
                sumv = left
            返回 // 重要，用于结束递归
        如果 left + v[t] <= V:
            left += v[t]
            dfs(t + 1)
            left -= v[t] // 回溯，恢复背包状态
        dfs(t + 1) // 不选择当前物品，继续递归

    方法 main:
        创建 Scanner对象 scanner 用于读取输入
        读取 V 和 n
        对于 i 从 0 到 n-1:
            读取 v[i]
        dfs(0) // 从第一个物品开始递归搜索
        打印 V - sumv // 输出最大未被选择的物品体积之和

java实现代码

import java.util.Scanner;

public class Main{
    static int N=30;
    static int n;
    static int V;
    static int[] v=new int[N];
    static int sumv=0;
    static int left=0;
   // static int[] op=new int[N];
    public static void dfs(int t){
        if(t>=n){
            if(left>sumv){
                sumv=left;
            }
            return;//很重要，没有会出错
        }
        if(left+v[t]<=V){
            left+=v[t];
            dfs(t+1);
            left-=v[t];
        }
        dfs(t+1);
    }
    public static void main(String[] args){
        Scanner scanner=new Scanner(System.in);
        V=scanner.nextInt();
        n=scanner.nextInt();
        for(int i=0;i<n;i++){
            v[i]=scanner.nextInt();
        }
        
        dfs(0);
        System.out.println(V-sumv);
    }
}