二叉树练习题（2024/6/3）-优快云博客

本文链接：https://blog.youkuaiyun.com/m0_74859128/article/details/139423476

1 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

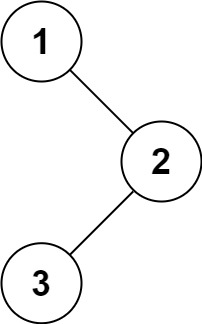
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

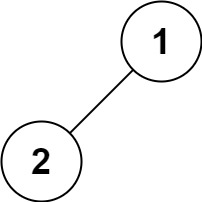
输入：root = [1,2]
输出：[1,2]

示例 5：

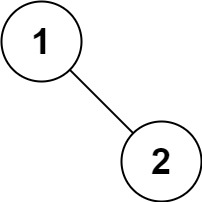
输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

递归思路：

递归算法通常可以遵循以下 “递归三部曲” 的解题思路：

确定递归函数的参数和返回值：确定递归函数需要传入的参数，通常包括当前问题的输入以及一些辅助参数，返回值通常是当前问题的解或者某种状态。
确定递归的终止条件：确定递归函数应该在什么情况下终止递归，返回结果或者不再进行递归调用。
确定每一层递归的逻辑：确定在每一层递归中应该做些什么，通常包括对参数的处理、递归调用自身及返回结果的处理。

确定递归函数的参数和返回值：
- 函数参数：
  - traversal(TreeNode* cur, vector<int>& vec)：当前处理的节点指针 cur 和存储节点值的数组引用 vec。
  - preorderTraversal(TreeNode* root)：二叉树的根节点 root。
- 返回值：
  - traversal 函数没有返回值（void），结果通过引用参数 vec 返回。
  - preorderTraversal 函数返回一个存储节点值的数组 vector<int>。
确定递归的终止条件：
- traversal 函数中，如果当前节点 cur 为空，直接返回，结束当前递归。
- preorderTraversal 函数中，如果根节点 root 为空，直接返回空数组。
确定每一层递归的逻辑：
- traversal 函数中，处理当前节点 cur 的值加入结果数组 vec，然后递归调用左子树和右子树。
- preorderTraversal 函数中，调用 traversal 函数开始递归前序遍历整棵树，最终返回遍历后的结果数组。

代码：

class Solution {
public:
    // 定义一个辅助函数，用来递归遍历二叉树并将节点值存入结果数组
    void traversal(TreeNode* cur, vector<int>& vec) {
        // 若当前节点为空，则返回
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中序遍历，将当前节点的值加入结果数组
        traversal(cur->left, vec);  // 递归遍历左子树
        traversal(cur->right, vec); // 递归遍历右子树
    }
    
    // 定义前序遍历函数，返回一个存储节点值的数组
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        // 从根节点开始遍历
        traversal(root, result); // 调用辅助函数，从根节点开始前序遍历
        return result;
    }
};

迭代法思路：

在迭代法中，我们使用一个栈来模拟递归调用的过程。具体来说，在遍历二叉树的过程中，我们将待访问的节点放入栈中，然后不断从栈中弹出节点，并按照规定的顺序访问节点的值，并将其子节点放入栈中。这样就可以实现对整个树的遍历。

以前序遍历为例，迭代法的思路是：

将根节点入栈。
当栈不为空时，循环执行以下操作：
- 弹出栈顶节点，访问其值，并将其右子节点（如果存在）和左子节点（如果存在）依次入栈。
当栈为空时，遍历结束

代码：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        
        // 如果根节点为空，直接返回空的结果数组
        if (root == NULL) return result;
        
        // 将根节点入栈
        st.push(root);
        
        // 当栈不为空时，继续迭代
        while (!st.empty()) {
            // 获取栈顶节点并出栈
            TreeNode* node = st.top();
            st.pop();
            
            // 将栈顶节点的值添加到结果数组中
            result.push_back(node->val);
            
            // 先处理右子树，因为出栈的顺序是先左后右，这样可以保证先遍历左子树
            if (node->right) st.push(node->right);
            
            // 再处理左子树
            if (node->left) st.push(node->left);
        }
        
        // 返回前序遍历的结果数组
        return result;
    }
};

2. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

递归代码：

 
class Solution {
public:
    //定义一个辅助函数，用来递归遍历二叉树并将节点值存入结果数组（中序遍历）
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == nullptr) return;
        traversal(cur->left, vec);      // 递归遍历当前节点的左子树
        vec.push_back(cur->val);        // 将当前节点的值加入结果数组
        traversal(cur->right, vec);     // 递归遍历当前节点的右子树
    }

   //定义中序遍历函数，返回一个存储节点值的数组
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);        // 开始中序遍历，将结果存入数组
        return result;
    }
};

迭代思路：

中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素

首先定义一个空的结果数组和一个栈，用来存储待访问的节点指针。
初始化当前节点为根节点。
进入循环，条件是当前节点不为空或者栈不为空。这是因为即使当前节点为空，栈中可能还有待处理的节点。
如果当前节点不为空，说明还有左子节点未访问，将当前节点入栈，并将当前节点移动到其左子节点。
如果当前节点为空，说明左子树已经访问完毕，从栈中取出节点进行处理：弹出栈顶节点，并将其值添加到结果数组中，然后将当前节点移动到其右子节点。
重复步骤3-5，直到当前节点为空且栈为空，遍历结束。

迭代代码：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;  // 定义结果数组
        stack<TreeNode*> st;  // 定义栈用来存储节点指针
        TreeNode* cur = root;  // 初始化当前节点为根节点
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) {  // 如果当前节点不为空
                st.push(cur);  // 将当前节点入栈
                cur = cur->left;  // 移动到左子节点
            } else {
                cur = st.top();  // 从栈中取出节点进行处理
                st.pop();  // 弹出栈顶节点
                result.push_back(cur->val);  // 将节点值加入结果数组
                cur = cur->right;  // 移动到右子节点
            }
        }
        return result;  // 返回结果数组
    }
};

3 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

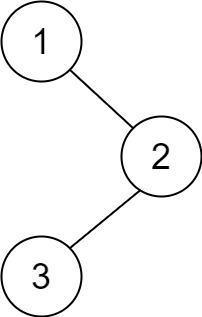
输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100

递归代码：

class Solution {
public:
    // 定义一个辅助函数，用来递归遍历二叉树并将节点值存入结果数组（后序遍历）
    void traversal(TreeNode *cur, vector<int>& vec) {
        if (cur == nullptr) return;
        traversal(cur->left, vec);   // 递归遍历当前节点的左子树
        traversal(cur->right, vec);  // 递归遍历当前节点的右子树
        vec.push_back(cur->val);     // 将当前节点的值加入结果数组
    }

    // 定义后序遍历函数，返回一个存储节点值的数组
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);     // 开始后序遍历，将结果存入数组
        return result;
    }
};

迭代代码：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;  // 定义一个栈用来存储节点指针
        vector<int> result;  // 定义一个结果数组
        if (root == NULL) return result;  // 如果根节点为空，直接返回结果数组
        st.push(root);  // 将根节点入栈
        while (!st.empty()) {  // 循环直到栈为空
            TreeNode* node = st.top();  // 取出栈顶节点
            st.pop();  // 弹出栈顶节点
            result.push_back(node->val);  // 将节点值加入结果数组
            if (node->left) st.push(node->left); // 如果存在左子节点，则将左子节点入栈
            if (node->right) st.push(node->right); // 如果存在右子节点，则将右子节点入栈
        }
        reverse(result.begin(), result.end()); // 将结果数组反转，得到左右中的顺序
        return result;  // 返回结果数组
    }
};

总结：

二叉树的三种常见遍历顺序包括先序遍历（Preorder Traversal）、中序遍历（Inorder Traversal）和后序遍历（Postorder Traversal），它们的特点如下：