C++优选算法十三 队列+宽搜BFS

关于树的题目

1.N 叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

解法:
算法思路:
层序遍历即可~
仅需多加一个变量，用来记录每一层结点的个数就好了。

class Solution {
public:
    vector<vector<int>> levelOrder(Node* root)
    {
        vector<vector<int>> vv;//记录最终结果
        if (root == nullptr)
            return vv;
        queue<Node*> qe;//层序遍历需要的队列
        qe.push(root);
        int n = 0;
        int i = 0;
        while (!qe.empty())
        {
            int sum = 0;
            vv.push_back({});//统计本层的节点
            n=qe.size();//求出本层与元素的个数
            while (n--)
            {
                Node* head = qe.front();
                vv[i].push_back(head->val);
                qe.pop();
                for (auto x : head->children)//让下一层节点入队
                {
                    qe.push(x);
                }
            }
            i++;
        }
        return vv;
    }
};

2.二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

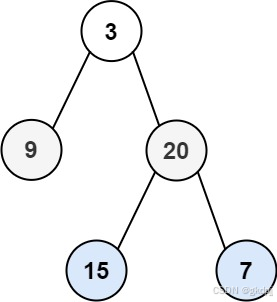
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

解法(层序遍历)
算法思路:
在正常的层序遍历过程中，我们是可以把一层的结点放在一个数组中去的。
既然我们有这个数组，在合适的层数逆序就可以得到锯齿形层序遍历的结果。
增加标志位，让偶数行的信息逆序。

class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) 
    {
        vector<vector<int>> vv;
        if(root==nullptr)
            return vv;
        queue<TreeNode*> qe;

        int n=0;
        qe.push(root);
        int m=1;
        while(qe.size())
        {
            n=qe.size();
            vector<int> vt;
            while(n--)
            {
                TreeNode*head=qe.front();
                qe.pop();
                vt.push_back(head->val);

                if(head->left)
                    qe.push(head->left);
                if(head->right)
                    qe.push(head->right);
            }
            //判断是否逆序
            if(m%2==0)
            {
                reverse(vt.begin(),vt.end());
            }
            vv.push_back(vt);
            m++;
        }
        return vv;
    }
};

 3. 二叉树最大宽度

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在  32 位 带符号整数范围内。

示例 1：

输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

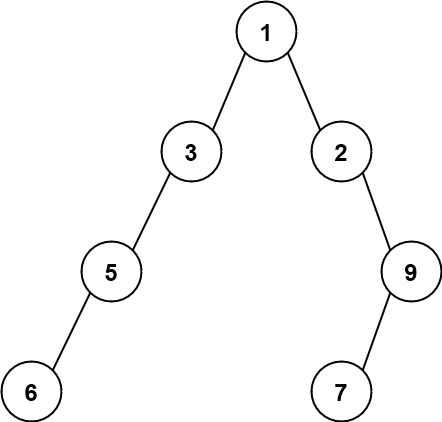
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

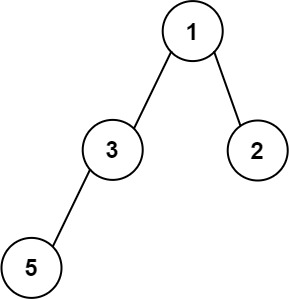
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

解法(层序遍历)
算法思路:
1.第一种思路(会超过内存限制)
既然统计每一层的最大宽度，我们优先想到的就是利用层序遍历，把当前层的结点全部存在队列里面，利用队列的长度来计算每一层的宽度，统计出最大的宽度。但是，由于空节点也是需要计算在内的。因此，我们可以选择将空节点也存在队列里面。
这个思路是我们正常会想到的思路，但是极端境况下，最左边一条长链，最右边一条长链，我们需要存几亿个空节点，会超过最大内存限制。

2.第二种思路(利用二叉树的顺序存储-通过根节点的下标，计算左右孩子的下标):
依旧是利用层序遍历，但是这一次队列里面不单单存结点信息，并且还存储当前结点如果在数组中存储所对应的下标。
这样我们计算每一层宽度的时候，无需考虑空节点，只需将当层结点的左右结点的下标相减再加 1即可。
但是，这里有个细节问题:如果二叉树的层数非常恐怖的话，我们任何一种数据类型都不能存下下标的值。但是没有问题，因为

• 我们数据的存储是一个环形的结构;
• 并且题目说明，数据的范围在 int这个类型的最大值的范围之内，因此不会超出一圈;
• 因此，如果是求差值的话，我们无需考虑溢出的情况。

class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) 
    {
        vector<pair<TreeNode*,unsigned int>> q;//用数组模拟队列
        q.push_back({root,1});
        unsigned int ret=0;

        while(q.size())
        {
            //更新这一层的宽度
            auto&[x1,y1]=q[0];
            auto&[x2,y2]=q.back();
            ret=max(ret,y2-y1+1);

            //让下层进队
            vector<pair<TreeNode*,unsigned int>> tmp;//让下层进入这个队列
            for(auto&[x,y]:q)
            {
                if(x->left)
                    tmp.push_back({x->left,y*2});
                if(x->right)
                    tmp.push_back({x->right,y*2+1});
            }
            q=tmp;
        }
        return ret;        
    }
};

4. 在每个树行中找最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

示例2：

输入: root = [1,2,3]
输出: [1,3]

解法(bfs)
算法思路:
层序遍历过程中，在执行让下一层节点入队的时候，我们是可以在循环中统计出当前层结点的最大值的。
因此，可以在 bfs 的过程中，统计出每一层结点的最大值。 

class Solution {
public:
    vector<int> largestValues(TreeNode* root) 
    {
        queue<TreeNode*> qe;
        vector<int> vv;
        if(root==nullptr)
            return vv;

        qe.push(root);
        int ret=INT_MIN;

        while(qe.size())
        {
            int n=qe.size();

            while(n--)
            {
                TreeNode*head=qe.front();
                ret=max(ret,head->val);
                qe.pop();
                if(head->left)
                    qe.push(head->left);
                if(head->right)
                    qe.push(head->right);
            }
            vv.push_back(ret);
            ret=INT_MIN;
        }

        return vv;
    }
};