map和set(四)——map和set的封装

于 2024-04-01 17:41:25 发布
阅读量783 收藏 21
点赞数 28
文章标签： 开发语言 c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_74515566/article/details/137074072
版权

前言

在一篇文章中我们对红黑树进行了简单的模拟实现

map和set(三)——红黑树-优快云博客

map和set的底层都是红黑树，而map和set中存储的键不同(map是键值对<K,V>；set是键K)，那么如何用一棵红黑树来封装出map和set这两种容器呢?

为适应不同的类型(键/键值对)，也就是泛型编程，之前的红黑树是RBTree<class K,class V>,额现在的红黑树RBTree<class K,class T>,当set调用红黑树时这个T会是K，当map调用时T则是pair<K,V>，是不是挺眼熟的(实际上就是之前学的模板)

一、红黑树模板(封装)

1.1参数模板以及红黑树节点修改

事不宜迟，先上代码

红黑树

template<class K,class T>
class RBTree

map

template<class K,class V>
class map
{

private:
	RBTree<K,pair<K,V>> _t;
};

set

template<class K>
class set
{

private:
	RBTree<K, const K> _t;
};

_t用红黑树模板类构造的对象，到时候可以调用红黑树里面的内容

既然红黑树的模板参数改了，那么红黑树节点的代码自然也要改

	enum Colour
	{
		RED,
		BLACK
	};

	template<class T>
	struct RBTreeNode
	{
		RBTreeNode<T>* _left;
		RBTreeNode<T>* _right;
		RBTreeNode<T>* _parent;
		Color _col;
		T _data;
		RBTreeNode(const T& data = T())
			:_left(nullptr)
			, _right(nullptr)
			, _parent(nullptr)
			, _col(RED)
			, _data(data)
		{}
	};

节点中存数据的对象相比之前的pair<K,V> _kv改成T _data，其它成员函数中new节点或者调用数据时也要记得修改为 data(data的类型)哦

1.2面对不同类型的比较

既然我们对参数模板修改了，且红黑树又是二叉搜索树(比根小的往左走，比根大的往右走)，不同的模板参数要对应不同的比较原则，对于set而言节点之间的比较只需要对比K就行了，那么map其节点之间的比较呢？map里面的pair是如何比较的？

我们不妨看一下库里面是怎么比较的

 first小就小，若first相等则second小就小

这明显不符合我们泛型编程的思路，如果按照这种写法，那么每传一次不同的模板参数，都要根据这个模板参数去实现一个新的比较大小的重载函数

我们可以面对不同的调用(比如map和set)，对其取出不同的值(map中pair里面的first，set中的K)然后再进行比较，具体的怎么取出不同的值可以在要调用红黑树的类中实现(map和set中)

红黑树

	template<class K, class T, class KeyOfT>
	class RBTree
	{
		typedef RBTreeNode<T> Node;

	public:
    //...

    }

 map

template<class K, class V>
class map
{
	struct MapKeyOfT
	{
		const K& operator()(const pair<K, V>& kv)//取出map中pair的first
		{
			return kv.first;
		}
	};
public:
	//...
private:
	RBTree<K, pair<K, V>,MapKeyOfT> _t;
};

set

template<class K>
class set
{
	struct SetKeyOfT
	{
		const K& operator()(const K& key)//取出set中的key
		{
			return key;
		}
	};
public:
	//...
private:
	RBTree<K, const K, SetKeyOfT> _t;
};

 在红黑树的成员函数中所有需要用到比较，或者需要取到所需要的"key"时可以调用对应的方法

可以通过KeyOfT实例化出对象，然后就可以调用所需要的取出"key"的方法，以Find为例吧(比较短)

当然其它的成员函数insert、erase啥的也要 

Node* Find(const T& data)
{
	KeyOfT kot;
	Node* cur = _root;
	while (cur)
	{
		if (kot(cur->_data) > kot(data))
		{
			cur = cur->_left;
		}
		else if (kot(cur->_data) < kot(data))
		{
			cur = cur->_right;
		}
		else
		{
			return cur;
		}
	}
	return nullptr;
}

二、迭代器的实现

2.1迭代器的定义及其构造函数

跟实现过程跟链表差不多，都是节点封装迭代器

template<class T>
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T> Self;
	Node* _pNode;

	RBTreeIterator(Node* pNode)
		: _pNode(pNode)
	{}
}

2.2解引用操作符*和箭头操作符->的重载

// 让迭代器具有类似指针的行为
T& operator*()
{
	return _pNode->_data;
}
T* operator->()
{
	return &_pNode->_data;
}

2.3重载==和！= 

// 让迭代器可以比较
bool operator!=(const Self& s)const
{
	return _pNode != s._pNode;
}
bool operator==(const Self& s)const
{
	return _pNode == s._pNode; ;
}

2.4重载++和-- 

跟链表不同的是++和--，毕竟链表和红黑树的结构不同，往前/后走的方法也就不同

红黑树该怎么往前/后走呢？首先我们要先知道一个点：红黑树中序打印是有序的

中序：左子树、根、右子树

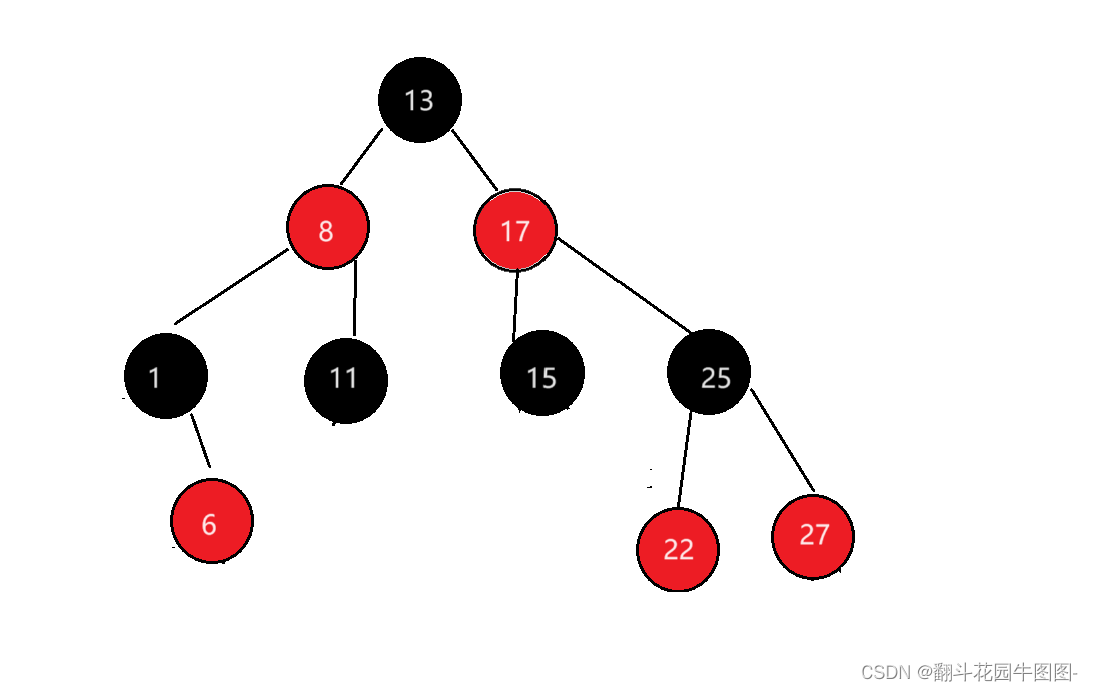
以++为例

假设it是用来遍历的一个节点， it指向的节点右子树不为空，下一个(也就是++后)就是右子树的最左节点

it指向的节点右子树为空，意味着这个节点的子树中序已经访问完了，下一个节点找祖先里面孩子等于父亲左的那个(以上图为例：6的下一个是8；15的下一个是17)

Self& operator++()
{
	if (_pNode->_right)//右不为空
	{
		//右子树的最左节点
		Node* subLeft = _pNode->_right;
		while (subLeft->_left)
		{
			subLeft = subLeft->_left;
		}
		_pNode = subLeft;
	}
	else
	{
		//右为空
		//祖先里面孩子是父亲左的那个
		Node* cur = _pNode;
		Node* parent = cur->_parent;
		while (parent&&cur == parent->_right)
		{
			cur = parent;
			parent = cur->_parent;
		}
		_pNode = parent;
	}
			return *this;
}

当然--和++类似

 如果当前节点(it)的左子树不为空，那么上一个节点(--后)应该找到左子树的最右节点

如果it的左子树为空，则上一个节点应该在祖先节点中孩子等于父亲右的那个

Self& operator--()
{
	if (_pNode->_parent==_pNode&&_pNode->_col==RED)//如果是头节点--那返回
	{
		_pNode = _pNode->_right;
	}
	else if (_pNode->_left)//左不为空
	{
		Node* subRight = _pNode->_left;
		while (subRight->_right)
		{
			subRight = subRight->_right;
		}
		_pNode = subRight;
	}
	else//左为空
	{
		Node* cur = _pNode;
		Node* parent = cur->_parent;
		//往上找
		while (parent&&cur == parent->_left)
		{
			cur = parent;
			parent = cur->_parent;
		}
		_pNode = parent;
	}
	return *this;
}

三、全部代码

myset.h

#pragma once
#include"RBTree.h"

namespace xxx
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K,const K, SetKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		bool insert(const K& key)
		{
			return _t.Insert(key);
		}

	private:
		RBTree<K, const K, SetKeyOfT> _t;
	};
	void test_set1()
	{
		set<int> s;
		int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
		for (auto e : a)
		{
			s.insert(e);
		}

		set<int>::iterator it = s.begin();
		while (it != s.end())
		{
			cout << *it << " ";
			++it;
		}
		cout << endl;
	}
}

mymap.h

#pragma once
#include"RBTree.h"

namespace xxx
{
	template<class K,class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K,V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<K,V>, MapKeyOfT>::iterator iterator;
		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}

		bool insert(const pair<K,V>& kv)
		{
			return _t.Insert(kv);
		}


	private:
		RBTree<K,pair<K,V>, MapKeyOfT> _t;
	};
	void test_map1()
	{
		map<int, int> m;
		int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
		for (auto e : a)
		{
			m.insert(make_pair(e, e));
		}

		map<int, int>::iterator it = m.begin();
		while (it != m.end())
		{
			cout << it->first << ":" << it->second << endl;
			++it;
		}
		cout << endl;
	}
}

 myRBTree.h

#pragma once
#include<iostream>
using namespace std;
namespace xxx
{
	enum Color
	{
		RED,
		BLACK
	};



	template<class T>
	struct RBTreeNode
	{
		RBTreeNode<T>* _left;
		RBTreeNode<T>* _right;
		RBTreeNode<T>* _parent;
		Color _col;
		T _data;
		RBTreeNode(const T& data = T())
			:_left(nullptr)
			, _right(nullptr)
			, _parent(nullptr)
			, _col(RED)
			, _data(data)
		{}


	};

	//迭代器
	template<class T>
	struct RBTreeIterator
	{
		typedef RBTreeNode<T> Node;
		typedef RBTreeIterator<T> Self;
		Node* _pNode;

		RBTreeIterator(Node* pNode)
			: _pNode(pNode)
		{}

		// 让迭代器具有类似指针的行为
		T& operator*()
		{
			return _pNode->_data;
		}
		T* operator->()
		{
			return &_pNode->_data;
		}

		Self& operator++()
		{
			if (_pNode->_right)//右不为空
			{
				//右子树的最左节点
				Node* subLeft = _pNode->_right;
				while (subLeft->_left)
				{
					subLeft = subLeft->_left;
				}
				_pNode = subLeft;
			}
			else
			{
				//右为空
				//祖先里面孩子是父亲的那个
				Node* cur = _pNode;
				Node* parent = cur->_parent;
				while (parent&&cur == parent->_right)
				{
					cur = parent;
					parent = cur->_parent;
				}
				_pNode = parent;
			}
			return *this;
		}

		Self& operator--()
		{
			if (_pNode->_parent==_pNode&&_pNode->_col==RED)//如果是头节点--那返回
			{
				_pNode = _pNode->_right;
			}
			else if (_pNode->_left)//左不为空
			{
				Node* subRight = _pNode->_left;
				while (subRight->_right)
				{
					subRight = subRight->_right;
				}
				_pNode = subRight;
			}
			else//左为空
			{
				Node* cur = _pNode;
				Node* parent = cur->_parent;
				//往上找
				while (parent&&cur == parent->_left)
				{
					cur = parent;
					parent = cur->_parent;
				}
				_pNode = parent;
			}
			return *this;
		}

		// 让迭代器可以比较
		bool operator!=(const Self& s)const
		{
			return _pNode != s._pNode;
		}
		bool operator==(const Self& s)const
		{
			return _pNode == s._pNode; ;
		}

		
	};








	template<class K,class T,class KeyOfT>
	class RBTree
	{
		typedef RBTreeNode<T> Node;

	public:
		typedef RBTreeIterator<T> iterator;
		iterator begin()
		{
			Node* subLeft = _root;
			while (subLeft && subLeft->_left)
			{
				subLeft = subLeft->_left;
			}

			return iterator(subLeft);
		}

		iterator end()
		{
			return iterator(nullptr);
		}
		
		// 在红黑树中插入值为data的节点，插入成功返回true，否则返回false
		// 注意：为了简单起见，本次实现红黑树不存储重复性元素
		bool Insert(const T& data)
		{
			if (_root == nullptr)
			{
				_root = new Node(data);
				_root->_col = BLACK;//根节点为黑色
				return true;
			}
			Node* parent = nullptr;
			Node* cur = _root;
			//找可以插入的节点
			KeyOfT kot;
			while (cur)
			{
				if (kot(cur->_data) < kot(data))
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (kot(cur->_data) > kot(data))
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			//开始插入
			cur = new Node(data);//新增节点为红色


			if (kot(parent->_data) < kot(data))
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			cur->_parent = parent;


			//判断要不要旋转
			while (parent && parent->_col == RED)
			{
				Node* grandfather = parent->_parent;
				if (parent == grandfather->_left)//父节点在左边，uncle在右边
				{
					Node* uncle = grandfather->_right;
					//情况一:uncle存在且为红
					if (uncle && uncle->_col == RED)
					{
						//变色
						parent->_col = uncle->_col = BLACK;
						grandfather->_col = RED;
						cur = grandfather;
						parent = cur->_parent;
					}
					else//情况二:uncle不存在或存在且为黑
					{
						if (cur == parent->_left)      //      g
						{                              //   p      u 
							RotateR(parent);           // c   
							parent->_col = BLACK;
							grandfather->_col = RED;
						}
						else
						{
							//双旋
							RotateL(parent);           //      g
							RotateR(grandfather);      //   p     u
							cur->_col = BLACK;         //    c
							grandfather->_col = RED;
						}
					}
				}
				else//父节点在右边,uncle在左边
				{
					Node* uncle = grandfather->_left;
					//情况一
					if (uncle && uncle->_col == RED)
					{
						parent->_col = uncle->_col = BLACK;
						grandfather->_col = RED;
						cur = grandfather;
						parent = cur->_parent;


					}
					else//不存在或者存在且为黑
					{
						if (cur == parent->_right)
						{
							RotateL(grandfather);           //    g
							parent->_col = BLACK;           //u       p
							grandfather->_col = RED;              //           c 
						}
						else
						{
							RotateR(parent);         //       g
							RotateL(grandfather);    // u           p
							cur->_col = BLACK;       //          c
							grandfather->_col = RED;
						}
						break;
					}
				}
			}
			_root->_col = BLACK;
			return true;
		}


		// 检测红黑树中是否存在值为data的节点，存在返回该节点的地址，否则返回nullptr
		Node* Find(const T& data)
		{
			KeyOfT kot;
			Node* cur = _root;
			while (cur)
			{
				if (kot(cur->_data) > kot(data))
				{
					cur = cur->_left;
				}
				else if (kot(cur->_data) < kot(data))
				{
					cur = cur->_right;
				}
				else
				{
					return cur;
				}
			}
			return nullptr;
		}


		/*获取红黑树最左侧节点*/
		Node* LeftMost()
		{
			Node* cur = _root;
			if (cur == nullptr)
			{
				return _root;
			}

			while (cur->_left)
			{
				cur = cur->_left;
			}

			return cur;
		}

		// 获取红黑树最右侧节点
		Node* RightMost()
		{
			Node* cur = _root;
			if (nullptr == cur)
			{
				return _root;
			}

			while (cur->_right)
			{
				cur = cur->_right;
			}

			return cur;
		}


		// 检测红黑树是否为有效的红黑树，注意：其内部主要依靠_IsValidRBTRee函数检测
		bool IsValidRBTRee()
		{
			if (_root && _root->_col == RED)
			{
				return false;
			}
			int refBlackNum = 0;//黑节点参考值
			Node* cur = _root;
			while (cur)
			{
				if (cur->_col == BLACK)
				{
					refBlackNum++;
				}
				cur = cur->_left;
			}
			return _IsValidRBTRee(_root, 0, refBlackNum);
		}


	private:
		bool _IsValidRBTRee(Node* cur, size_t blackCount, size_t refBlack)
		{
			if (cur == nullptr)
			{
				if (refBlack != blackCount)
				{
					cout << "黑色节点不相等" << endl;
					return false;
				}
				return true;
			}
			if (cur->_col == RED && cur->_parent->_col == RED)
			{
				cout << "存在连续红色节点" << endl;
				return false;
			}
			if (cur->_col == BLACK)
				blackCount++;
			return _IsValidRBTRee(cur->_left, blackCount, refBlack)
				&& _IsValidRBTRee(cur->_right, blackCount, refBlack);
		}
		void RotateL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subR->_left;

			parent->_right = subRL;
			if (subRL)
				subRL->_parent = parent;

			subR->_left = parent;
			Node* ppnode = parent->_parent;
			parent->_parent = subR;

			if (parent == _root)
			{
				_root = subR;
				subR->_parent = nullptr;
			}
			else
			{
				if (ppnode->_left == parent)
				{
					ppnode->_left = subR;
				}
				else
				{
					ppnode->_right = subR;
				}
				subR->_parent = ppnode;
			}
		}
		void RotateR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;

			parent->_left = subLR;
			if (subLR)
				subLR->_parent = parent;

			subL->_right = parent;

			Node* ppnode = parent->_parent;
			parent->_parent = subL;

			if (parent == _root)
			{
				_root = subL;
				subL->_parent = nullptr;
			}
			else
			{
				if (ppnode->_left == parent)
				{
					ppnode->_left = subL;
				}
				else
				{
					ppnode->_right = subL;
				}
				subL->_parent = ppnode;
			}
		}
	private:
		Node* _root = nullptr;
	};


}

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值