本文详细介绍了三种排序算法。快速排序有递归式（hoare、挖坑法、前后指针版本）和非递归实现；归并排序包含递归和非递归方式，递归需注意空间开辟，非递归要修正边界；计数排序通过统计元素出现个数，利用相对映射节省空间，将数存到数组。
一、快速排序
1、递归式
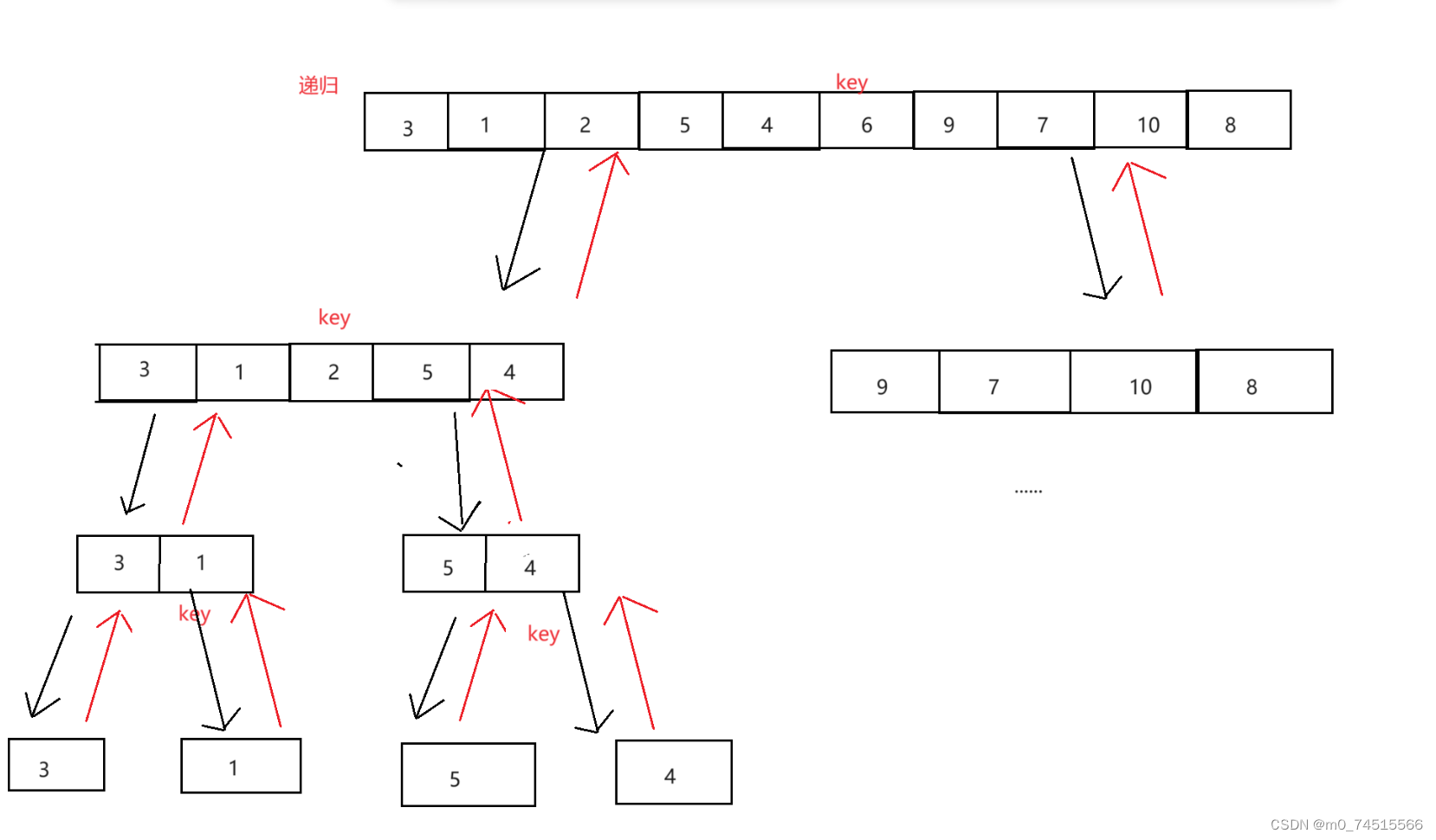
//递归
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
//一趟
//hoare
int keyi = PartSort1(a, begin, end);
//挖坑法
//int keyi = PartSort2(a, begin, end);
//双指针
//int keyi = PartSort3(a, begin, end);
//一趟走完，key会走到正确位置上 所以要排序的范围变成 [begin，keyi-1] [keyi+1，end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi+1, end);
}(1)hoare
思路：
先找key，一般是最左边的元素
右边先往前找比key小的值，右边的值都要大于key嘛，小的值就要移到左边
同理，左边大于key的值就要移到右边，左边往后找比key大的值，找到后和右边比key小的值交换
交换后继续找，直到L和R相遇，交换一下key和相遇位置的值
相遇的位置一定比key小，按照前面的思路：R先走，R停下来时的位置的值比key小，然后相遇时L去跟R相遇，所以相遇位置一定会比key小
如果是L先走的话相遇位置一定比key大
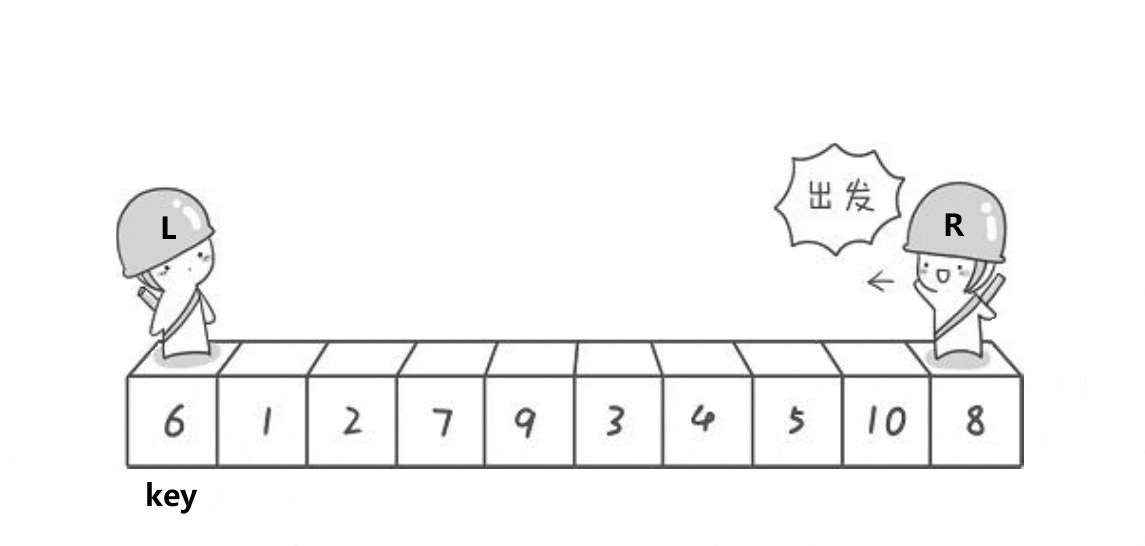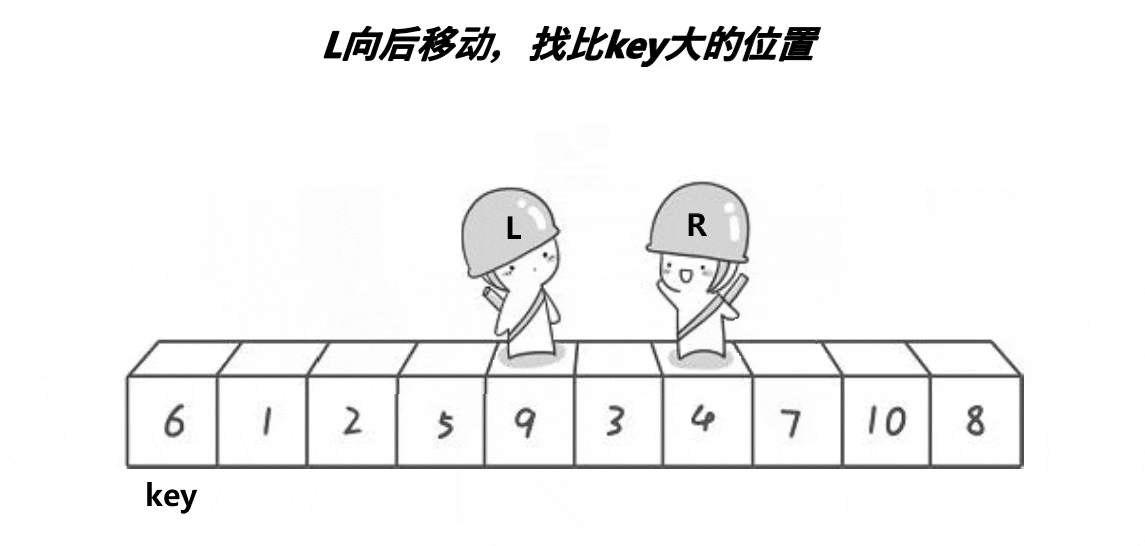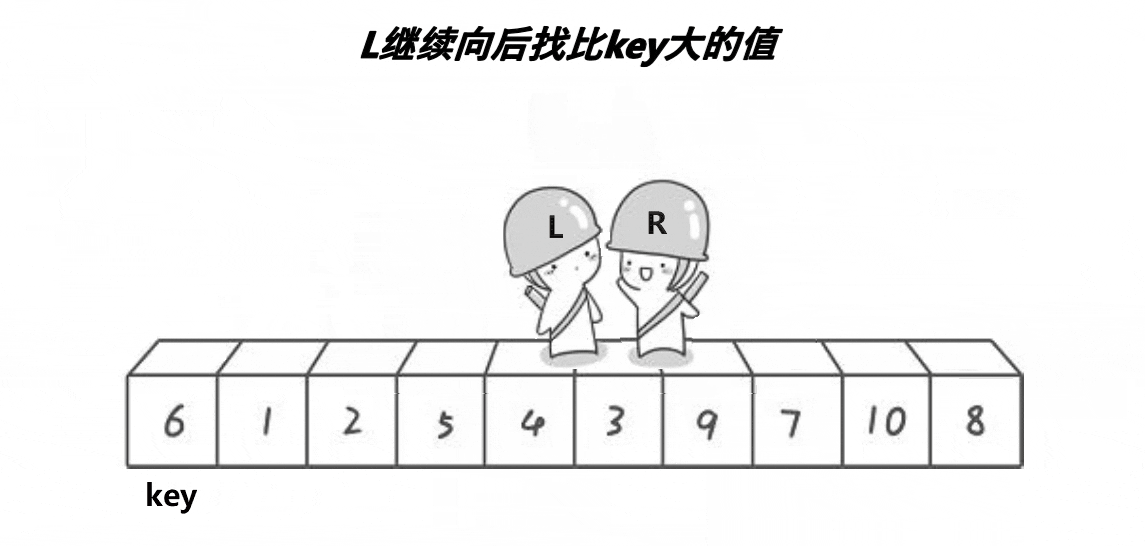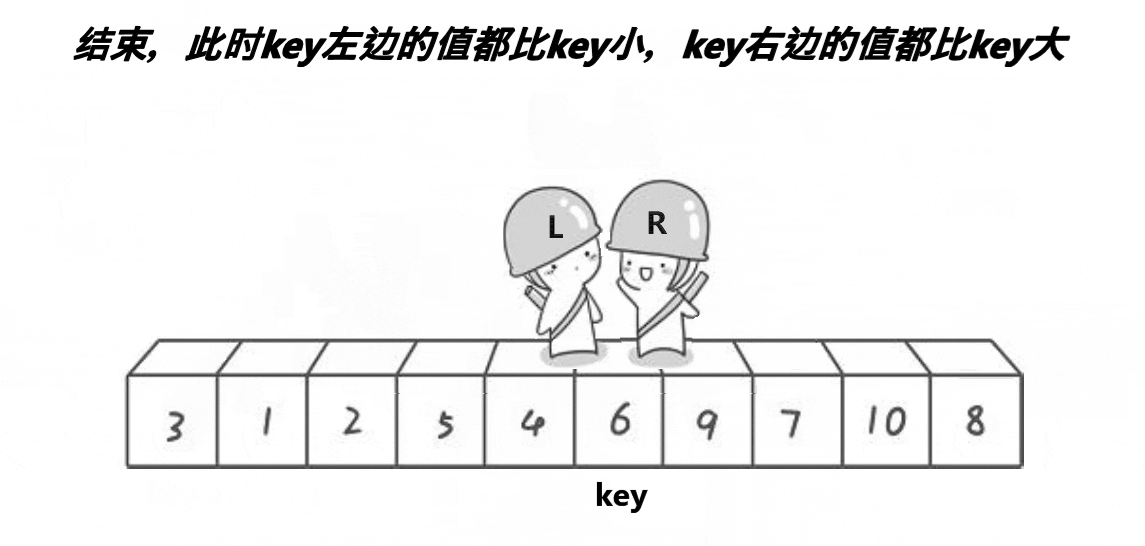
实现
key是数组中的一个元素，找到这个元素需要下标，定义一个变量为keyi存放key元素的下标
根据上面的思路要一直找一直换，直到两边相遇while循环搞定
然后右边找小左边找大，也是while循环，注意循环条件
先判断left是否小于right，再判断右边的值是否大于等于key，都满足right就往前走
停下来说明右边找到比key小的值，左边同理，停下来找到比key大的值
交换一下左右边各自找到的值
当左右两边相遇时交换一下相遇位置(这里下标是left是right都可以，毕竟已经相遇了)
//hoare版
int PartSort1(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
//找小的 如果右边大就往左走
while (left < right && a[right] >= a[keyi])
{
right--;
}
//找大的
while (left < right && a[left] <= a[keyi])
{
left++;
}
//走到这说明右边遇到小于key的；且左边遇到大于key的
//交换
swap(&a[left], &a[right]);
}
//走到这说明left 和 right 相遇 交换key和相遇坐标对应的元素
swap(&a[keyi], &a[left]);
return left;
}(2)挖坑法
思路
和上面的思路相似，但是要先挖个坑，比如在key位置挖坑，创建一个变量把key存起来
还是右边找小，找到把那个小的填到刚才那个坑里
填完右边多了一个坑，左边找大的，找到后填右边的那个坑
填完左边又多了个坑......
边填边挖直到相遇，相遇时是个坑位，然后把我们刚才存的key放到坑里
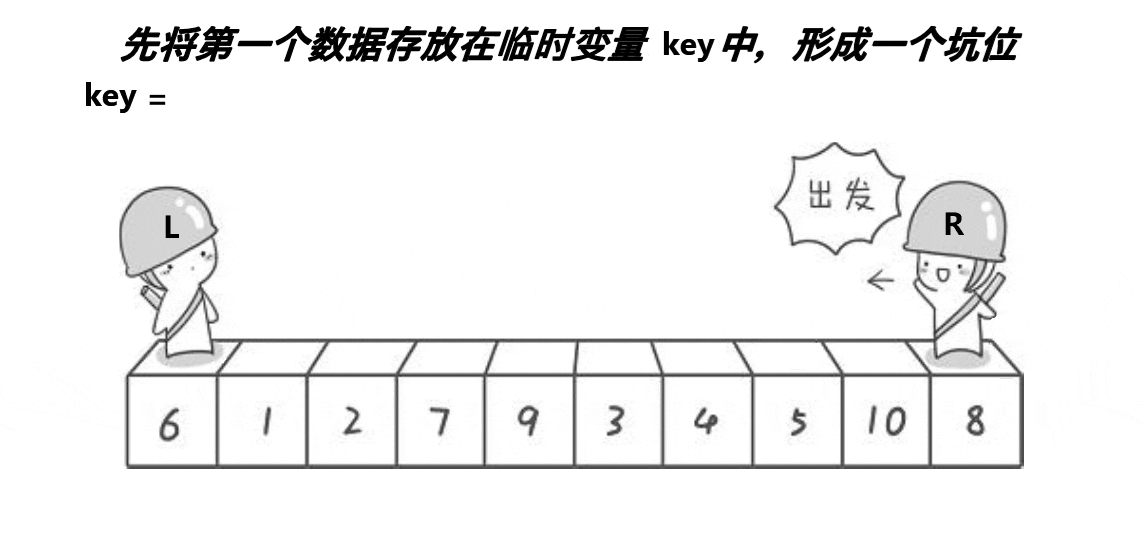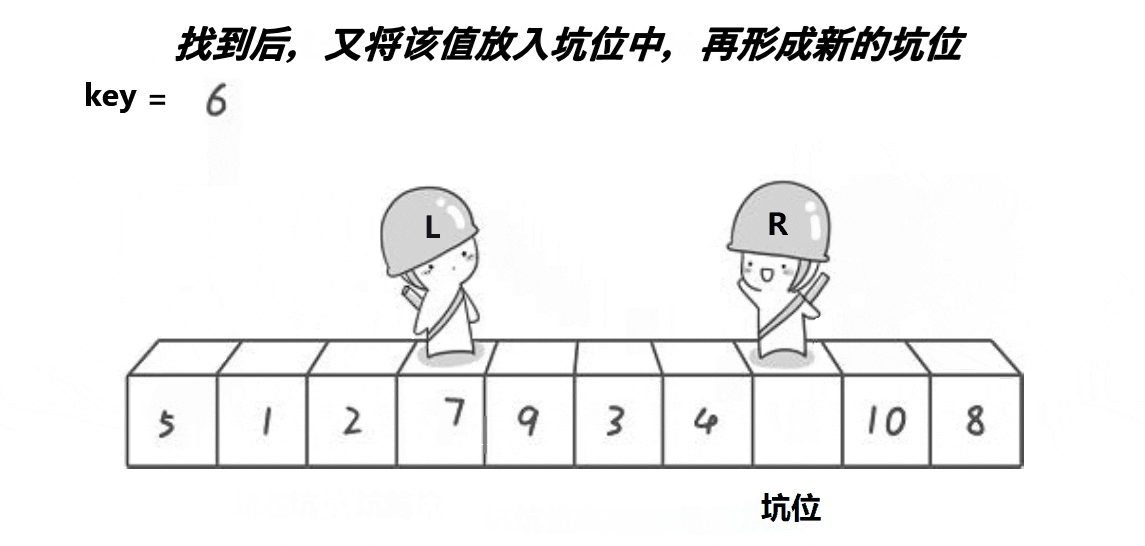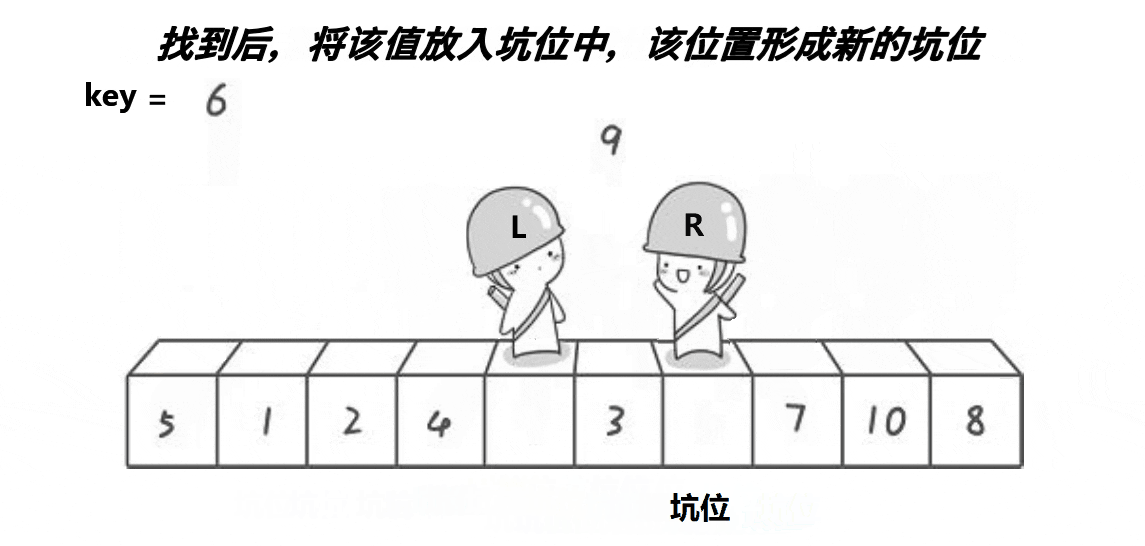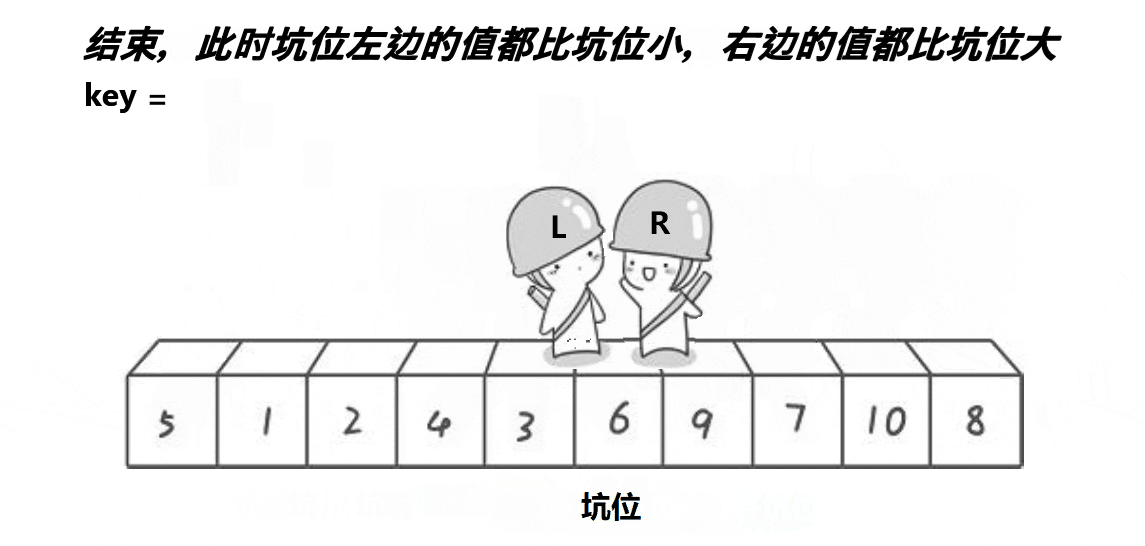
实现
int PartSort2(int* a, int left, int right)
{
//保存key的值
int key = a[left];
int hole = left;//挖坑
while (left<right)
{
//右边先走找小
while (left<right&&a[right]>=key)
{
right--;
}
//找到了 把值填入坑
a[hole] = a[right];
//形成新的坑
hole = right;
//左边走找大
while (left < right && a[left] <= key)
{
left++;
}
//找到填坑
a[hole] = a[left];
//出现新坑
hole = left;
}
//相遇还有坑 把key的值填入坑
a[hole] = key;
return hole;
}(3)前后指针版本
思路
还是先整个key
慢指针指向第一个元素，快指针指向第二个元素
前指针找小，后指针找大，找到后交换
快指针走出数组(越界)说明该换的已经换了
将慢指针指向的元素和key换一下
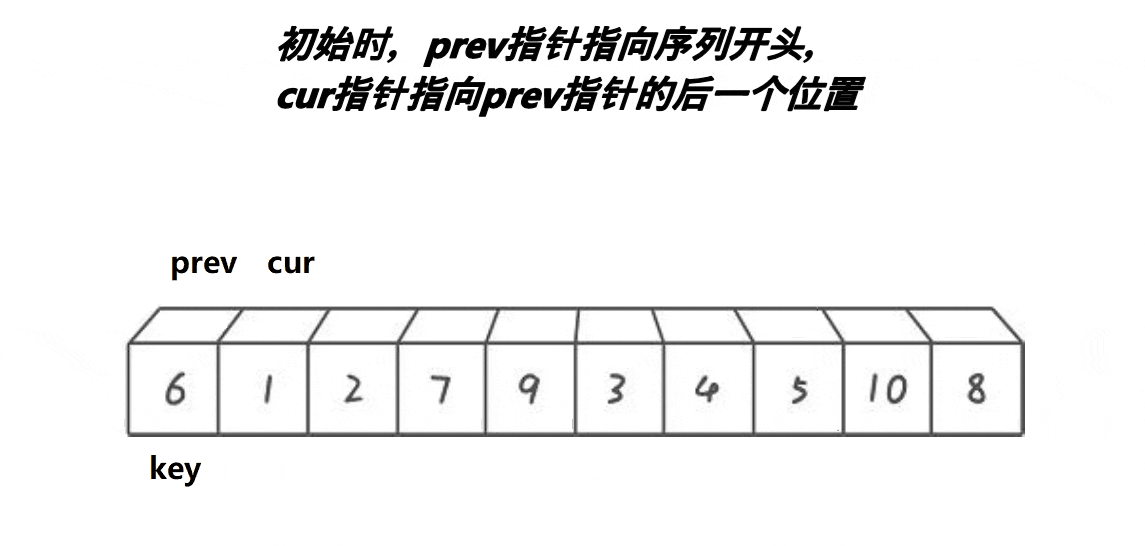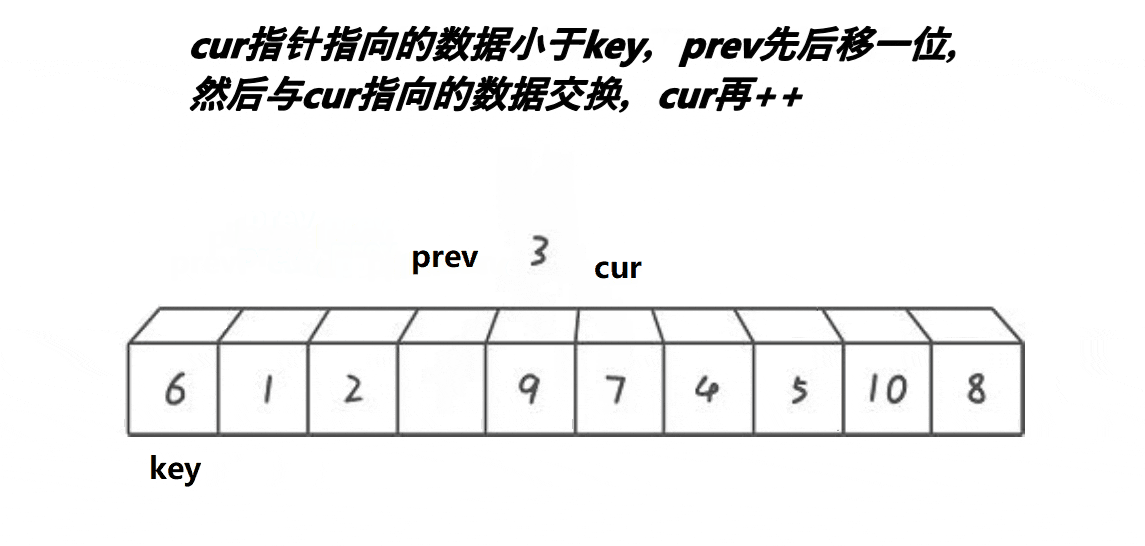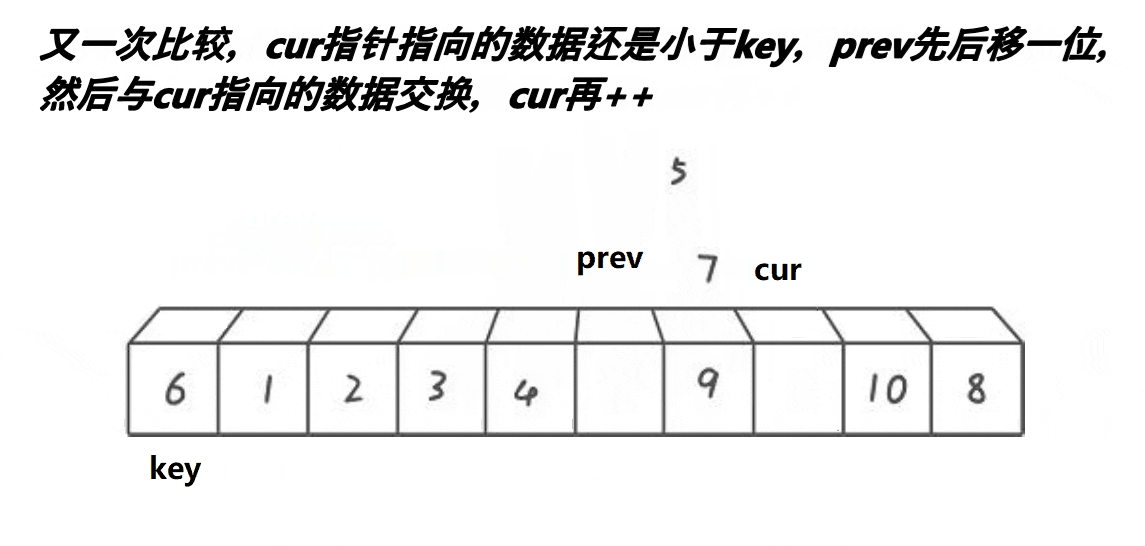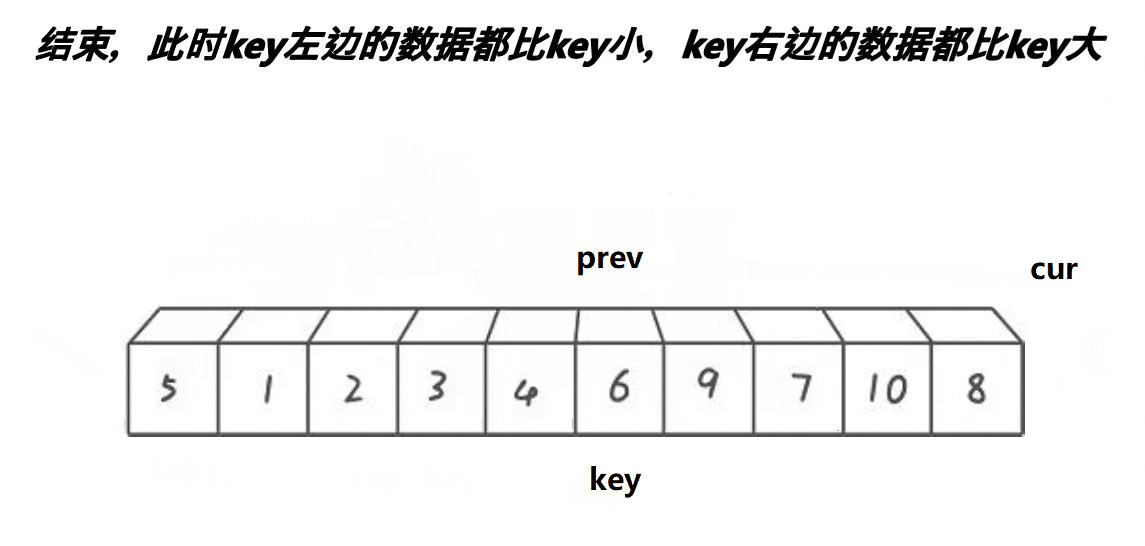
实现
int PartSort3(int* a, int left, int right)
{
int keyi = left;
int slow = left, fast = left + 1;
//快指针走出数组结束
while (fast <= right)
{
//如果快指针指向的值小于key 慢指针先向后走 如果快慢指针不相等 交换两个值
//快指针再往后走
if (a[fast] < a[keyi]&&slow!=fast)
{
slow++;
swap(&a[slow], &a[fast]);
}
//上面条件满不满足快指针都要往后走
fast++;
}
//交换key和慢指针
swap(&a[keyi], &a[slow]);
return slow;
}
2、非递归
思路
非递归需要用栈来辅助实现
把递归(进入函数)看成入栈；区间不存在就视为递归的返回
实现
栈的特点是后进先出，所以我们应该先入右再入左，先走一趟排序
栈非空就走排序
走完一趟后又分有左区间和右区间
还是先入右区间再入左区间，如此反复
区间不存在就不用入了
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
STInit(&st);
//栈是后进先出的 所以按照之前的逻辑 应该先入右边 再入左边
STPush(&st, end);
STPush(&st,begin);
while (!STEmpty(&st))
{
//后入先出
int left = STTop(&st);
STPop(&st);
//先入后出
int right = STTop(&st);
STPop(&st);
int keyi = PartSort1(a, left, right);//一趟
if (keyi + 1 < right)
{
STPush(&st, right);
STPush(&st, keyi+1);
}
if (left < keyi - 1)
{
STPush(&st, keyi-1);
STPush(&st, left);
}
}
STDestroy(&st);
}二、归并排序
1、递归
思路
归并排序也是不断分左区间和右区间
如果左半区间有序，右半区间也有序，归并就是依次比较两区间的数取小的尾插
要尾插到一个新数组然后再拷贝回来
无序的话就继续分割
直到分割到左半区间有序或者只有一个元素(也可以看作有序)，右半区间同理
有序和只有一个元素就又可以归并了(取小尾插)
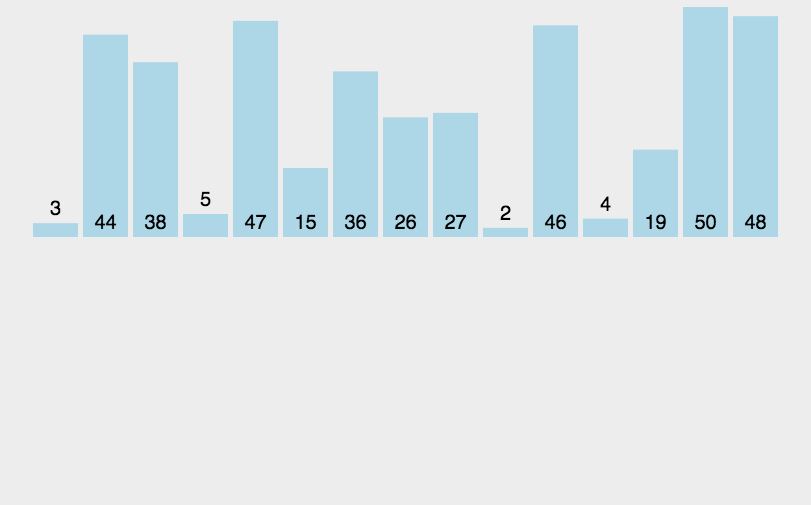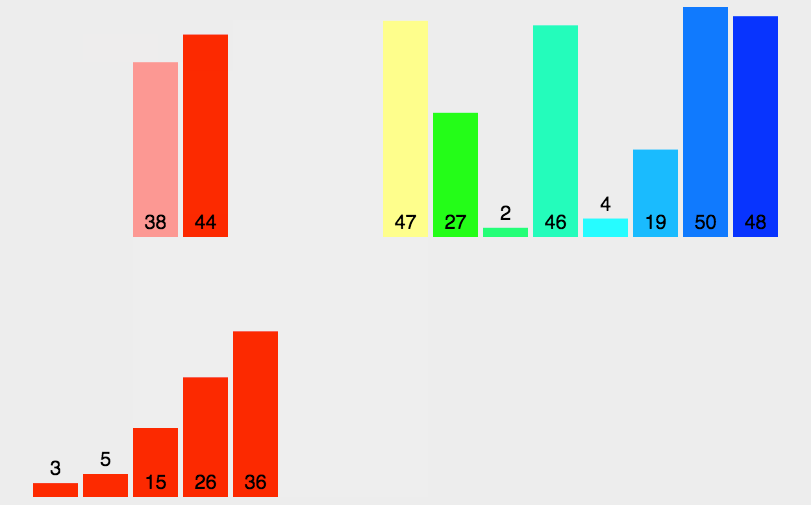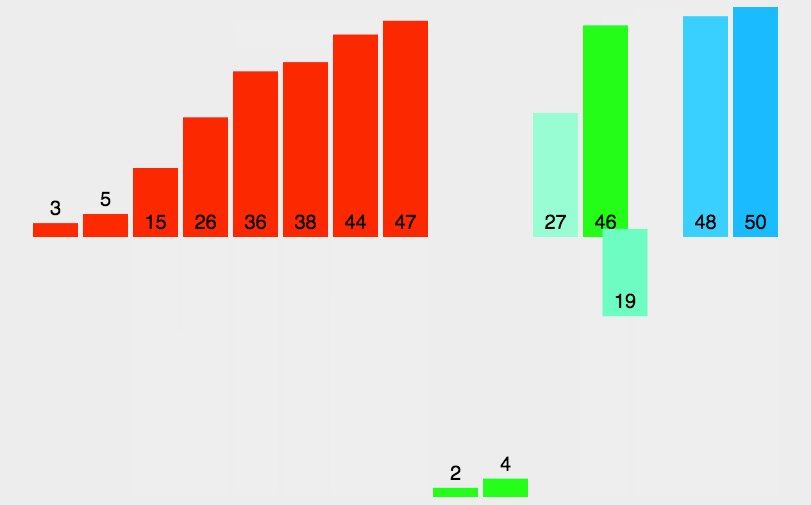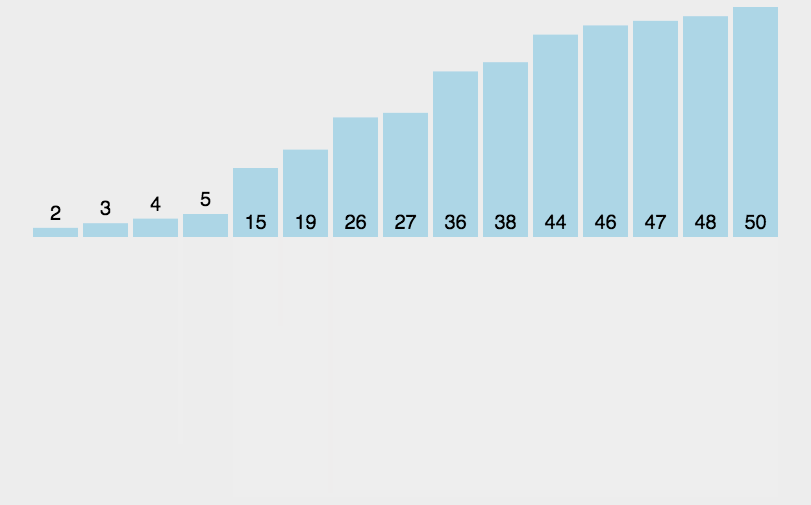
实现
开辟一个空间让我们尾插
注意递归要在子函数中进行，不然每次递归都会开辟新空间
按照前面的思路分到单个元素就不用再分了，也就是不用递归
怎么分呢？先定义一个变量mid存数组的中间元素的下标
然后首元素下标begin到下标mid分为一组(左区间)，下标mid+1到尾元素end分为一组(右区间)
这就分割完了
还要定义一个刚才开辟的数组tmp里面的下标index
然后就进行尾插
判断一下:哪个小哪个入tmp
判断条件是有一个结束就全结束
这就会导致存在一个数组没完全插入的情况，这时候需要判断两个区间是否完全插入
最后把tmp的内容拷贝回去
void mergeson(int* a, int* tmp, int begin, int end)
{
if (end <= begin)
return;
int mid = (begin + end) / 2;
//左右递归
mergeson(a, tmp, begin, mid);
mergeson(a, tmp, mid+1,end);
//分割
int begin1 = begin, end1 = mid;
int begin2 = mid+1, end2 = end;
int index = begin;//tmp里的下标
//一个结束就都结束
while (begin1<=end1 &&begin2<=end2)
{
//分割完哪个小先入tmp
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
//分割后还没录入tmp的
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//把tmp里面排好的拷贝到原来的位置上
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
//子函数 去递归
//不然每次进入函数都会开辟新空间
mergeson(a,tmp,0,n-1);
free(tmp);
}2、非递归
思路
这个排序递归怎么用非递归实现呢？
倒过来看递归分割会变成1个元素和1个元素归并
归并完就变成2个元素和两个元素归并
到最后全部的左区间和全部的右区间归并
那么我们可以定义一个gap，gap等于1就是11归并，等于二就是22归并......以此类推
但是这样的情况只适用于数组元素为2的次方个，一旦数组非2次方个，会越界
所以我们需要修正边界(越界的组就不用归并了)
实现
根据前面的思路如何实现一一归并到nn归并，还有一个小组归并完怎么到另一个小组去呢？
也就是如何分区间
gap最开始是1，gap不能大于n，每次gap需要乘等2
访问数组元素需要用下标，分割数组，也要从数组下标开始分
分组可以i到i+gap-1一组，i+gap到i+2*gap-1一组
我们可以用i=0来做初始下标，for循环每次i加等2*gap来模拟跳到另一个小组
注意：
分区间之后要判断是否越界，判断完才进行归并
[begin1,end1] [begin2,end2]
如果end1 越界或者 begin2 越界 不需要归并了
如果只有end2越界了就修正下标，下标不能超过n，end2的下标改为n-1
然后就到了归并
归并完拷贝回原数组要注意之前递归时写的是拷贝2*gap个
如果是修正完边界还拷贝2*gap个的话会造成越界访问
end2-begin1+1就是数据个数，但是前面begin1++了
所以应该拷贝end2-i+1个
//归并非递归
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += gap * 2)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i+gap, end2 = i + gap*2 - 1;
//越界
if (begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
//归并
int index = i;//tmp里的下标
while (begin1 <= end1 && begin2 <= end2)
{
//分割完哪个小先入tmp
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
//分割后还没录入tmp的
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//把tmp里面排好的拷贝到原来的位置上
memcpy(a + i, tmp + i, (end2-i+1) * sizeof(int));
}
gap *= 2;
}
free(tmp);
}三、计数排序
思路
统计每个元素出现的个数，然后从小到大依次把数存放到数组中
这里为了节省空间我们可以用到相对映射，找到最小值让其对应到下标为0的位置开始
实现
void CountSort(int* a, int n)
{
//找出最大/小值
int max = a[0], min = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
//开空间
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
//初始化
memset(count, 0, sizeof(int) * range);
//统计数字出现次数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//排序
int j = 0;
for (int i = 0; i < n; i++)
{
//count数组中元素是多少就录入多少个
while (count[i]--)
{
a[j++] = i + min;
}
}
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
