数据结构----二叉树

---

一、什么是二叉树？

二叉树的概念

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分 。
二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点 。

二、基本操作（注：图片资料来源b站相关学习视频截图，侵权删）

定义

插入结点

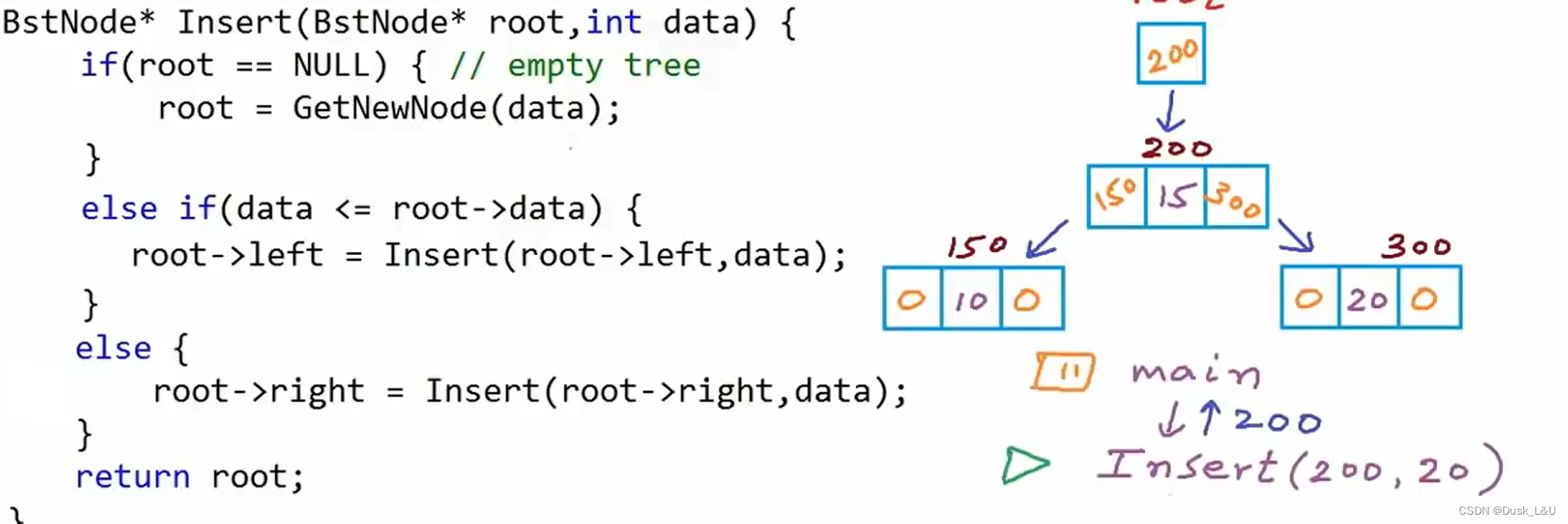
主函数

查找最大值和最小值

有两种方式：
1）迭代，使用循环来找到

最大值同理，找右子树（记得考虑树空和非空两种情况）

2）递归
return FindMin(root->left);

二叉树的高度

结点深度：到根节点的距离
结点高度：到最深叶结点的距离
树的高度：树中任意结点的最大深度

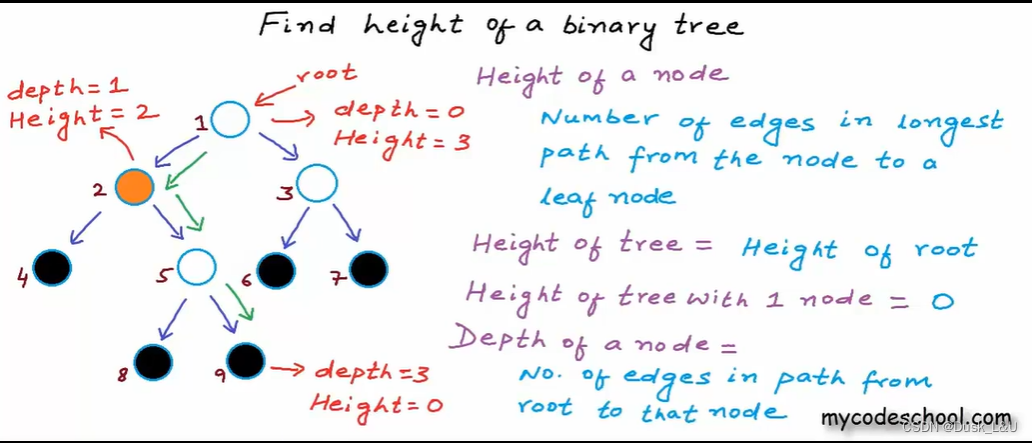
递归计算左子树和右子树的高度

二叉树的遍历—广度优先vs深度优先

层序遍历访问顺序：一层一层向下，从左到右

广度优先方式：对于任意结点，我们首先访问该节点的所有的孩子，然后才去访问它的孙子结点—层序遍历

深度优先方式：对于任意结点，完成整个孩子的子树后，再到下一个孩子（即完成左子树/右子树，所有深度后再去遍历右子树/左子树，根结点访问顺序随意）—前、中、后序遍历

访问一个结点是读取、处理或者打印结点的数据

访问一个结点时，可以把该结点的孩子的引用或者地址放入一个队列之中，这样我们就可以在稍后访问他们。
使用队列有两件事，首先，我们从一个结点开始移动，但不会丢失对它的孩子的引用，因为我们保存了结点的引用，然后因为队列的一个先进先出的结构，所以首先被发现的那个结点，首先插入的结点会被首先访问，因此，我们可以得到我们想要的顺序。在这种方法中，任意时刻，我们把一组地址放在内存中，放在队列之中，而不是仅使用一个结点指针来移动。

层次遍历（使用了头文件 #include《queue》,C++标准模板库）

前中后序遍历

时间复杂度：O（n);
空间复杂度：O(h);----h是树的高度

---

三、总结

二叉树性质：
性质1：二叉树的第i层上至多有2i-1（i≥1）个节点。
性质2：深度为h的二叉树中至多含有2h-1个节点。
性质3：若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1 。
性质4：具有n个节点的满二叉树深为log2n+1。
性质5：若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），那么，对于编号为i（i≥1）的节点：
当i=1时，该节点为根，它无双亲节点 。
当i>1时，该节点的双亲节点的编号为i/2 。
若2i≤n，则有编号为2i的左节点，否则没有左节点 。
若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点 。