最近面试经常遇到的一些算法题,总结一下。
常见的排序算法
2025.2.19腾讯一面、2025.2.21字节一面
快速排序
算法思路分析
方法其实很简单:分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。这里可以用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边(即i=1),指向数字6。让哨兵j指向序列的最右边(即=10),指向数字。

首先哨兵j开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵j先出动,这一点非常重要(请自己想一想为什么)。哨兵j一步一步地向左挪动(即j–),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。


现在交换哨兵i和哨兵j所指向的元素的值。交换之后的序列如下:
6 1 2 5 9 3 4 7 10 8


到此,第一次交换结束。接下来开始哨兵j继续向左挪动(再友情提醒,每次必须是哨兵j先出发)。他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动的,他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下:
6 1 2 5 4 3 9 7 10 8
第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下:
3 1 2 5 4 6 9 7 10 8



到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。之后以6为边界,递归地去“探测”左右子数组,这样就是快速排序的全过程了。
时间复杂度分析
时间复杂度最好情况nlog(n)
最坏情况:log(n2)
对应场景:
- 场景:每次分区后一个子数组长度为 0,另一个为 n−1(例如数组已有序,且始终选择第一个元素为基准)
具体代码实现
//快速排序核心思路
//过选择一个基准元素(这里是数组的第一个元素),将数组分为两部分:一部分小于基准元素,
// 另一部分大于基准元素,然后递归地对这两部分进行排序。
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){return;}
//i 从左向右移动,寻找大于基准元素的元素。
i=low;
//j 从右向左移动,寻找小于基准元素的元素。
j=high;
//temp就是基准位,选择当前数组分段的第一个元素
temp = arr[low];
while (i<j) {
//先看右边,依次往左递减
while (temp<=arr[j]&&i<j) {
j--;
}
//再看左边,依次往右递增
while (temp>=arr[i]&&i<j) {
i++;
}
//如果满足条件则交换
if (i<j) {
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
//最后将基准数与i和j相等位置的数字交换
arr[low] = arr[i];
arr[i] = temp;
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
public static void main(String[] args) {
int[] arr = {10, 7, 8, 9, 1, 5,1};
System.out.println("排序前: " + Arrays.toString(arr));
quickSort(arr, 0, arr.length - 1);
System.out.println("排序后: " + Arrays.toString(arr));
}堆排序
算法思路分析
什么是堆
堆是一种叫做完全二叉树的数据结构,可以分为大根堆,小根堆,而堆排序就是基于这种结构而产生的一种程序算法。
堆的分类
大根堆:每个节点的值都大于或者等于他的左右孩子节点的值

小根堆:每个结点的值都小于或等于其左孩子和右孩子结点的值

两种结构映射到数组为:
大根堆:

小根堆

映射关系如下:
父节点下标i--->左孩子:2*i+1, 右孩子:2*i+2
子节点下标i--->(i-1)/2 (注意得到的结果向下取整)
排序思路
1.首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
注意:升序用大根堆,降序就用小根堆(默认为升序)
构造堆
构造堆的步骤如下:
首先我们给定一个无序的序列,将其看做一个堆结构,一个没有规则的二叉树,将序列里的值按照从上往下,从左到右依次填充到二叉树中。

构建堆首先要找到最后一个非叶子节点所在的位置,对应的索引为arr.len / 2 -1,对于上图数组长度为5,最后一个非叶子节点为5/2-1=1,即为6这个节点
找到最后一个非叶子节点后,比较它的左右节点中最大的一个的值,是否比他大,如果大就交换位置。
在这里5小于6,而9大于6,则交换6和9的位置
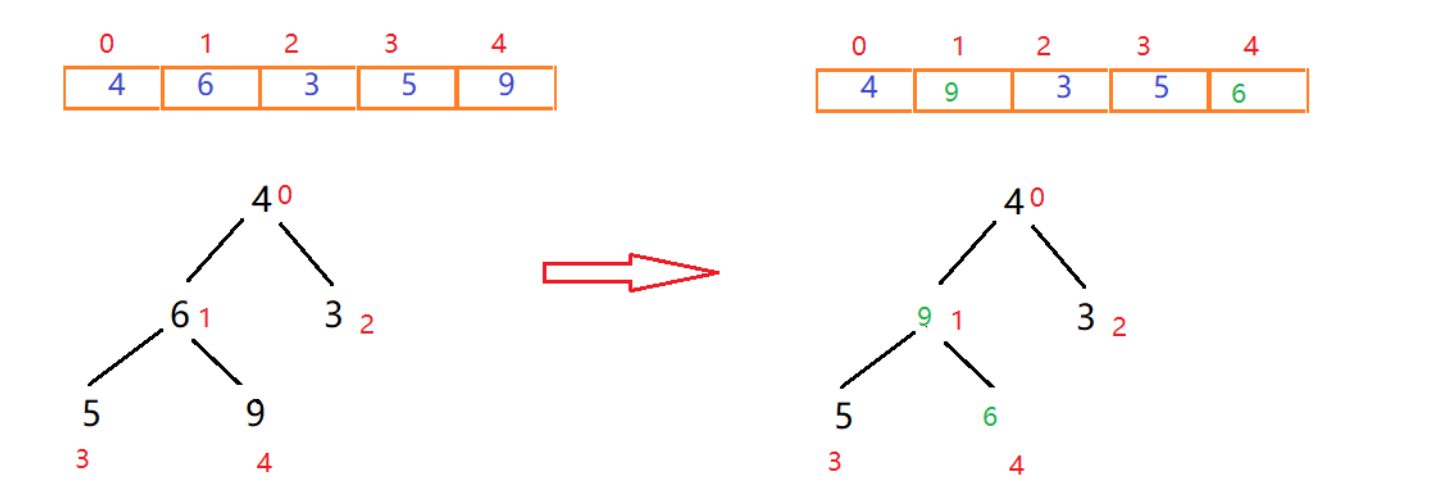
找到下一个非叶子节点4,用它和它的左右子节点进行比较,4大于3,而4小于9,交换4和9位置

此时发现4小于5和6这两个子节点,我们需要进行调整,左右节点5和6中,6大于5且6大于父节点4,因此交换4和6的位置

此时我们就构造出来一个大根堆,下来进行排序
排序
首先将顶点元素9与末尾元素4交换位置,此时末尾数字为最大值。排除已经确定的最大元素,将剩下元素重新构建大根堆
一次交换重构如图:

此时元素9已经有序,末尾元素则为4(每调整一次,调整后的尾部元素在下次调整重构时都不能动)
二次交换重构如图:

最终排序结果:

由此,我们可以归纳出堆排序算法的步骤:
1. 把无序数组构建成二叉堆。
2. 循环删除堆顶元素,移到集合尾部,调节堆产生新的堆顶。
当我们删除一个最大堆的堆顶(并不是完全删除,而是替换到最后面),经过自我调节,第二大的元素就会被交换上来,成为最大堆的新堆顶。
正如上图所示,当我们删除值为9的堆顶节点,经过调节,值为6的新节点就会顶替上来;当我们删除值为6的堆顶节点,经过调节,值为5的新节点就会顶替上来.......
由于二叉堆的这个特性,我们每一次删除旧堆顶,调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶,反复调节二叉堆,所得到的集合就成为了一个有序集合,
时间复杂度分析
堆排序是不稳定的排序,空间复杂度为O(1),平均的时间复杂度为O(nlogn),最坏情况下也稳定在O(nlogn)
具体代码实现
/*
原理:将数组构建成最大堆(或最小堆),然后逐个取出堆顶元素并调整堆。
时间复杂度:
最好情况:O(n log n)
平均情况:O(n log n)
最坏情况:O(n log n)
空间复杂度:O(1)(原地排序)
稳定性:不稳定
*/
// 堆排序入口方法
public static void heapSort(int[] arr) {
int n = arr.length;
// 构建最大堆
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 排序
for (int i = n - 1; i > 0; i--) {
// 将堆顶元素(最大值)与堆的最后一个元素交换
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 调整堆,使其重新满足最大堆的性质
heapify(arr, i, 0);
}
}
// 调整堆
private static void heapify(int[] arr, int n, int i) {
int largest = i; // 初始化最大值为当前节点
int left = 2 * i + 1; // 左子节点
int right = 2 * i + 2; // 右子节点
// 如果左子节点大于当前最大值,更新最大值
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点大于当前最大值,更新最大值
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大值不是当前节点,交换并递归调整
if (largest != i) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
// 递归调整子树
heapify(arr, n, largest);
}
}
// 测试
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6, 7};
System.out.println("排序前: " + Arrays.toString(arr));
heapSort(arr);
System.out.println("排序后: " + Arrays.toString(arr));
}冒泡排序
算法思路分析
冒泡排序基本思想
通过对待排序序列从前向后(从下标较小的元素开始),依次对相邻两个元素的值进行两两比较,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就如果水底下的气泡一样逐渐向上冒。
示例分析
待排序数组:3,9,-1,10,20
(1)3,9,-1,10,20 ----3跟9比较,不交换
(2)3,-1,9,10,20 ----9比 -1大,所以9跟 -1交换
(3)3,-1,9,10,20 ----9跟10比较,不交换
(4)3,-1,9,10,20 ----10跟20比较,不交换
第一轮过后,将20这个最大的元素固定到了最后的位置
因为20的位置已经固定,所以只对前4个进行排序即可:
(1)-1,3,9,10,20 ----3比 -1大,进行交换
(2)-1,3,9,10,20 ----3跟9比较,不交换
(3)-1,3,9,10,20 ----9跟10比较,不交换
第二轮过后,将第二大的元素固定到了倒数第二个位置
10和20的位置已经确定,只需对前三个进行排序
(1)-1,3,9,10,20 ----3和-1比较,不交换
(2)-1,3,9,10,20 ----3和9比较,不交换
第三轮过后,将第三大的元素位置确定
只对前两个元素进行排序
(1)-1,3,9,10,20 ----3和-1比较,不交换
第四轮过后,将第四大的元素位置确定,此时总共5个元素,已经排序好4个,从而最后一个自然而然就是排好序的了
时间复杂度分析
| 最好 | O(n) | 输入数组已完全有序 | 1轮扫描,n-1次比较 |
| 最坏 | O(n²) | 输入数组完全逆序 | Σ(n-1 + n-2 + ... +1) = n(n-1)/2 |
| 平均 | O(n²) | 随机排列数组 | 约需要n²/2次比较 |
具体代码实现
public class BubbleSort {
public void bubbleSort(int[] arr) {
if (arr == null || arr.length <= 1) return;
int n = arr.length;
// 外层循环控制排序轮次(n-1轮)
for (int i = 0; i < n - 1; i++) {
boolean swapped = false; // 优化标记
// 内层循环进行相邻元素比较(每轮少比较i个已排序元素)
for (int j = 0; j < n - 1 - i; j++) {
// 前 > 后时交换(实现升序排序)
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
swapped = true; // 标记发生交换
}
}
// 本轮未发生交换说明已完全有序,提前终止
if (!swapped) break;
}
}
// 交换数组元素
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] arr = {5, 2, 9, 1, 5, 6};
new BubbleSort().bubbleSort(arr);
System.out.println(Arrays.toString(arr)); // 输出:[1, 2, 5, 5, 6, 9]
}
}

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










