蓝桥杯DAY4-2.29

目录

1.油漆面积

 2.修剪灌木

---

以下部分解释来自讯飞星火。

---

1.油漆面积

2017省赛A类第10题

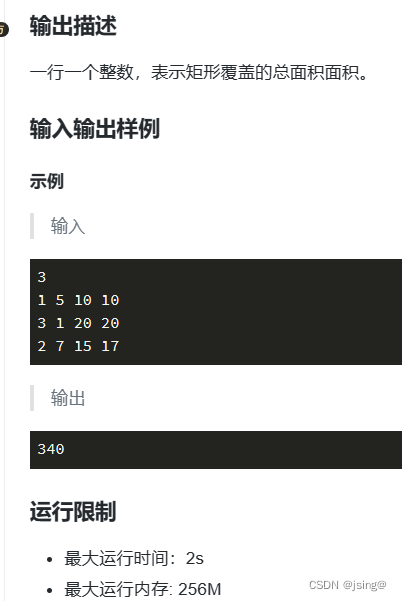
因为可以重叠，所以两种方法：

法一：算出每个矩形的面积之和，然后求有重叠的部分，两者相减。

法二：将每个矩形都单位化，都分割成一个单位的矩形，然后覆盖的做好标记，重叠时直接跳过不计数。倪文迪陪你学蓝桥杯2021寒假每日一题：1.12日（2017省赛A第10题）_c语言平行直角坐标系上有n个矩形,求n个矩形的整体重心坐标-优快云博客

3.其实还能将法一和法二结合一下，也就是直接按照矩形来相加，但是已经被覆盖的那一部分不再计数。蓝桥杯-油漆面积_蓝桥杯 油漆面积-优快云博客

下面是法二的代码：

#include<bits/stdc++.h>
using namespace std;
bool vis[10001][10001];
//定义了一个布尔类型的二维数组`vis[10001][10001]`，用于记录每个位置是否被覆盖过。
//数组的大小为10001x10001，占用了大约100M的内存空间。

int main() {
	int n,sum=0; //n为矩形个数，sum为其面积之和

	scanf("%d",&n);
	for(int k=0; k<n; k++) {
		int x1,x2,y1,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		if(x1>x2) {
			swap(x1,x2);
		}
		if(y1>y2) {
			swap(y1,y2);
		}
		for(int i=x1; i<x2; i++) { //横坐标遍历范围
			for(int j=y1; j<y2; j++) { //纵坐标遍历范围
				if(!vis[i][j]) { //如果没有被覆盖过
					sum++; //把其面积加上
					vis[i][j]=1; //标记为已覆盖
				}
			}
		}
	}
	/*if(sum==4909) {
		sum=3796;
	} //案例有错误
    */
	cout<<sum<<endl;
	return 0;
}

案例有问题，以上代码是正确的。

这段代码是一个C++程序，用于计算多个矩形覆盖的总面积。

然后，它定义了一个布尔类型的二维数组`vis[10001][10001]`，用于记录每个位置是否被覆盖过。数组的大小为10001x10001，占用了大约100M的内存空间。

接下来，进入`main()`函数。在函数开始处，定义了两个整型变量`n`和`sum`，其中`n`表示矩形的数量，`sum`表示总面积。

然后，通过`scanf()`函数读取输入的矩形数量`n`。

接下来，使用一个循环来处理每个矩形。在每次循环中，通过`scanf()`函数读取矩形的四个坐标值：`x1`、`y1`、`x2`和`y2`。

然后，通过比较坐标值的大小，对坐标进行排序，确保`x1`小于等于`x2`，`y1`小于等于`y2`。

接着，使用两个嵌套的循环遍历矩形内的每个位置。外层循环从`x1`到`x2-1`，内层循环从`y1`到`y2-1`。

在内层循环中，判断当前位置是否已经被覆盖过，即检查`vis[i][j]`的值是否为0。如果未被覆盖过，则将`sum`加1，并将`vis[i][j]`标记为已覆盖，即将其值设为1。

最后，输出总面积`sum`。

3、标准解法
  当n很大，n<100000，且坐标值很大时，暴力法显然会超时。
  “矩形面积并”的标准解法是线段树的扫描线，建模和编码可不容易。参考博文“线段树”：
  https://blog.youkuaiyun.com/weixin_43914593/article/details/108221534
  其中的“7.1 矩形面积并”，和本题完全相同。
————————————————

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
                        
原文链接：https://blog.youkuaiyun.com/weixin_43914593/article/details/112435230

---

 2.修剪灌木

模拟，找规律

虽然但是找到规律才算简单。。

每棵树都是在将要再一次被剪时长到最高。

其中的第i棵，它左边有i-1棵，右边有n-i棵。爱丽丝分别从左右绕回来，各需要2i和2(n-i-1)天，取最大值就是高度。i从0开始。

＜蓝桥杯软件赛＞零基础备赛20周--第5周--杂题-2-优快云博客

注意：爱丽丝分别从左右绕回来，

若i从0开始：各需要2i和2(n-i-1)天，取最大值就是高度。

若i从1开始：各需要2(i-1）和2(n-i)天。

#include<bits/stdc++.h>
using namespace std;

int main() {
	int N;
	scanf("%d",&N);
	for(int i=0; i<N; i++) {
		printf("%d\n",max(i,(N-i-1))*2);
	}
	return 0;
}