Codeforces Round 987 (Div. 2)(E，补题+续写上一篇)

我就不覆上文章了，这里丢一个链接Problem - E - Codeforces

题意:对于题意我是读了很久才懂，但是别人说的都很简洁明了我还是需要自己去推一遍样例，构造一棵最小深度的完全二叉树与给定的树同构。

同构的意思我去查了一下，好像就是节点随意交换排序后跟另一颗树完全相同就行(欢迎反驳一起讨论)

思路:考虑从给的树去构造完全二叉树。我们求的是某个节点假设为根节点时操作成为完全二叉树的最小深度。

假设某个节点的儿子>=2

这里给读者画个图方便理解👇

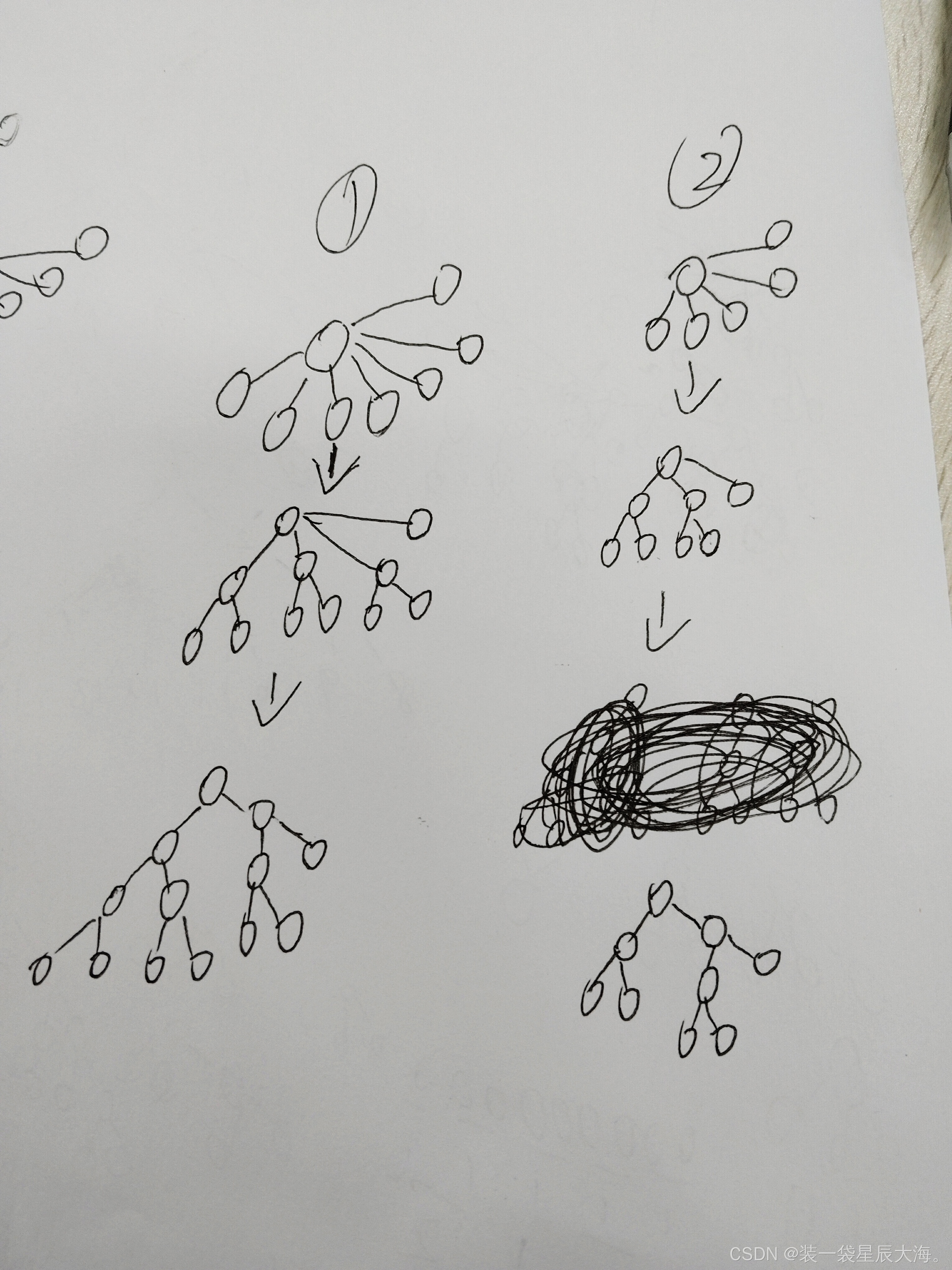
假设当前要求的是上面树的某两个节点操作后的最小深度，最理想的是操作后会变成最下面的样子

可以发现要删掉两个儿子就要加一个节点a，让那两个儿子(深度最小的两个儿子)成为节点a的儿子，然后如果根节点有超过2个的节点a就要再加一个节点b，让两个节点a(深度最小的两个节点a)去成功这个节点b的儿子，然后如果根节点有超过2个节点b就要继续....这样。可以发现这两个节点操作后的最小深度为3

我们肯定不是要去模拟然后求出答案，这里只是让读者知道我26行写的代码为什么就会求出来。当然到根节点也要这样操作。

然后根节点肯定会有<=2个儿子，每个儿子节点就都会有设为当前节点为根节点时操作成为完全二叉树的最小深度的值a和值b。这样答案就是max(a,b)+1。

假设某个节点的儿子<=1的话，这个情况就很简单。这里直接看代码吧。

#include<bits/stdc++.h>
#define ed '\n'
#define IOS ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
using namespace std;
const int g=1e6+10;
vector<int>ve[g];
void solve()
{
    int n=0;cin>>n;
    for(int i=2;i<=n;i++)
    {
        int x=0;cin>>x;
        ve[x].push_back(i);
    }
    
    auto dfs=[&](auto dfs,int now,int fa)->int
    {
        if(ve[now].size()==0)return 0;   //儿子为0的情况
        priority_queue<int,vector<int>,greater<int>>qu;  //小根堆，这里肯定是要从深度最小的开始构建，图上已经说明。
        
        for(auto to:ve[now])qu.push(dfs(dfs,to,now));
        
        if(qu.size()==1)return qu.top()+1;//儿子为1的情况。
        else                              //儿子>=2的情况
        {
            while(qu.size()>=2)           //求出以当前节点为根节点操作成完全二叉树的最小深度。
            { 
                int k1=qu.top();qu.pop();
                int k2=qu.top();qu.pop();
                qu.push(max(k1,k2)+1);
            }
            return qu.top();             //返回这个值到它的父亲。
        }
    };
    
    cout<<dfs(dfs,1,0)<<ed;
    for(int i=1;i<=n;i++)ve[i].clear();
    return ;
}
signed main()
{
    IOS;
    
    int t=1;
    
    cin>>t;
    
    while(t--)
    {
        solve();
    }
    return 0;
}

完结。

附:思路借鉴于Codeforces Round 987 (Div. 2)（前五道）_penchick and bbq buns-优快云博客

大佬。