非递归遍历二叉树

二叉树结构

//二叉树结构
typedef struct BitNode{
    char data;
    struct BitNode *lchild; //左孩子
    struct BitNode *rchild;  //右孩子
}BitNode,*BiTree;

二叉树的非递归遍历，要用到栈先进后出的结构

栈结构如下

//栈的结构
typedef struct tree
{
    int top;//栈顶
    int base;//栈底
    BiTree *arr; //因为我们后序遍历要判断地址是否为空，所以我们用二级指针
}stank;

   初始化栈

//初始化栈
void Initie(stank &s){
    s.arr=(BiTree*) malloc (Max*sizeof(BitNode));
   if(!s.base)
       exit(0);
    s.top=s.base=0;
}

判断栈是否为空

//判断栈是否为空
int Empty(stank &s){
    if(s.top==s.base)
        return 0;
    else
        return 1;
}

入栈

//入栈
void Enter(stank &s,BiTree T){
    s.arr[s.top]=T;
            s.top++;
}

出栈

//出栈
void Go_out(stank &s){
        s.top--;
}

构建一颗二叉树

//构建一颗二叉树
BiTree CreeatBiTree(){
    BiTree T;
    char ch;
    scanf("%c",&ch);
    getchar(); //吸收空格
    if(ch=='0')  //当输入0时，代表某有孩子
    {
        T=NULL;
    }
    else
    {
        T=(BiTree) malloc (sizeof(BitNode));
        T->data=ch;
        printf("请输入%c的左孩子：",T->data);
        T->lchild=CreeatBiTree();
        printf("请输入%c的右孩子：",T->data);
        T->rchild=CreeatBiTree();
    }
    return T;
}

基本的框架已经构建完成，现在讲解遍历

一、先序遍历，根左右

先序遍历，我们一开始先让根节点进栈，在将根节点出栈，剩下的一次进栈，先进后出

所以理解成根节点不用栈的结构

因为我们把根节点A一进栈就出栈，所以现在B出栈完，C在出战

void Preorder(BiTree L){
    stank s;
    BiTree B;
    //给B开辟空间
    B=(BiTree) malloc (sizeof(BitNode));
    Initie(s);//初始化栈
    if(L==NULL){
        return;
    }
    else
    {
    //先把根节点进栈
        Enter(s,L);
        while(Empty(s)){//栈空退出循环
            B=s.arr[s.top-1];//B来接收
            printf("%c ",B->data);
            //出栈
            Go_out(s);
            if(B->rchild)
            {
                Enter(s, B->rchild);
            }
            if(B->lchild)
            {
                Enter(s, B->lchild);
            }
        }
    }
}

二、中序遍历，左根右

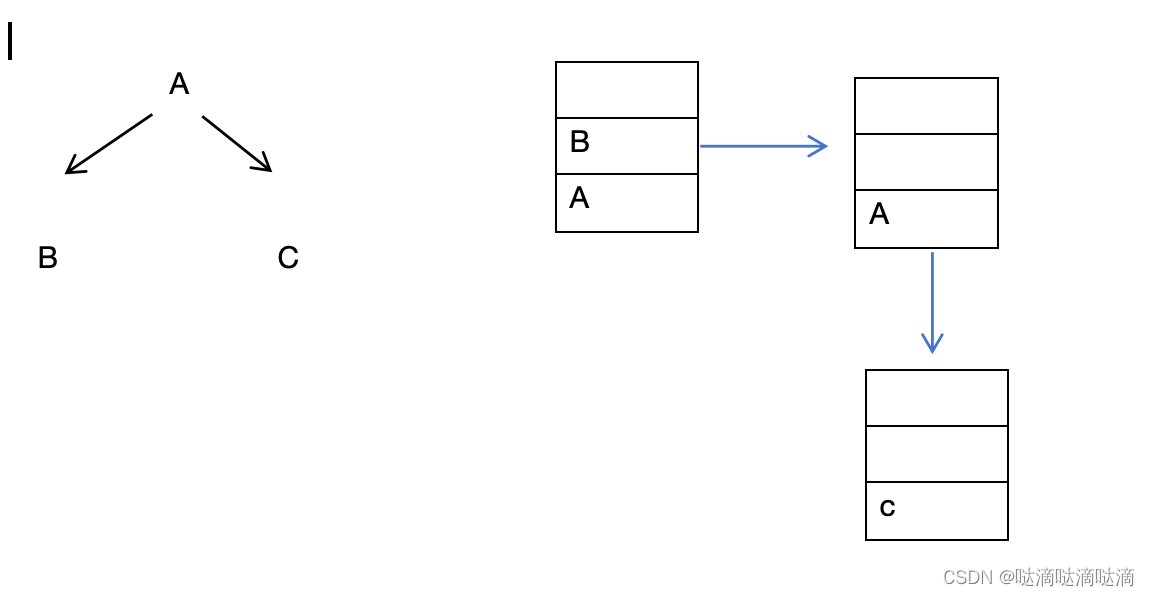
先将根节点A入栈，在依次递归将A的左孩子进栈，一直把左孩子进栈完，在依次从下往上出栈，出栈一个就要判断右孩子是否为空

在依次往上将做孩子的右孩子入栈

//中序遍历,左根右
void InOrder(BiTree L){
    BiTree B;
    stank s;
    Initie(s); //初始化栈
    if(!L){
        return;
    }
    B=L;
    while(B!=NULL || Empty(s))
    {
        while(B!=NULL)
        {
            Enter(s,B);//进栈
            B=B->lchild;//左孩子全部进栈
        }//退出循环是指针指向的左孩子为空
        B=s.arr[s.top-1];
        printf("%c ",B->data);
        Go_out(s);//出栈
        B=B->rchild;//指向右孩子
    }
}

三、后序遍历，左右根

还是先把根节点入栈，在把左孩子全部入栈，然后依次出栈左孩子，出栈一次，就要判断左孩子是否有右孩子，有右孩子就要入栈

//后序遍历
void Postorder(BiTree L){
    if(!L){
        return;
    }
    BiTree B=L;
    BiTree H=NULL;
    stank s;
    Initie(s);//初始化栈
    while(B ||Empty(s))
    {
        while(B)
        {
            Enter(s, B);
            B=B->lchild;
        }
       BiTree C=s.arr[s.top-1];
        if( C->rchild==NULL || C->rchild==H )
        {
            printf("%c ",C->data);
            Go_out(s);
            H=C;//记录当前结点
            C=NULL;
        }
        else
        {
            B=C->rchild;
        }
    }
}

注意这个条件if( C->rchild==NULL || C->rchild==H )

当只有三个值时，就剩A未出栈，A的右孩子也不为null，所以要记录好A的右孩子，这样就可以进入if条件

 

四、全部代码如下

//二叉树的非递归遍历，前，中，后
#include <stdio.h>
#include <stdlib.h>
#define Max 100
//二叉树结构
typedef struct BitNode{
    char data;
    struct BitNode *lchild; //左孩子
    struct BitNode *rchild;  //右孩子
}BitNode,*BiTree;

//栈的结构
typedef struct tree
{
    int top;//栈顶
    int base;//栈底
    BiTree *arr;
}stank;

//初始化栈
void Initie(stank &s){
    s.arr=(BiTree*) malloc (Max*sizeof(BitNode));
   if(!s.base)
       exit(0);
    s.top=s.base=0;
}

//判断栈是否为空
int Empty(stank &s){
    if(s.top==s.base)
        return 0;
    else
        return 1;
}
//入栈
void Enter(stank &s,BiTree T){
    s.arr[s.top]=T;
            s.top++;
}
//出栈
void Go_out(stank &s){
        s.top--;
}
//构建一颗二叉树
BiTree CreeatBiTree(){
    BiTree T;
    char ch;
    scanf("%c",&ch);
    getchar(); //吸收空格
    if(ch=='0')  //当输入0时，代表某有孩子
    {
        T=NULL;
    }
    else
    {
        T=(BiTree) malloc (sizeof(BitNode));
        T->data=ch;
        printf("请输入%c的左孩子：",T->data);
        T->lchild=CreeatBiTree();
        printf("请输入%c的右孩子：",T->data);
        T->rchild=CreeatBiTree();
    }
    return T;
}

//先序遍历，根左右
void Preorder(BiTree L){
    stank s;
    BiTree B;
    //给B开辟空间
    B=(BiTree) malloc (sizeof(BitNode));
    Initie(s);
    if(L==NULL){
        return;
    }
    else
    {
    //先把根节点进栈
        Enter(s,L);
        while(Empty(s)){//栈空退出循环
            B=s.arr[s.top-1];//B来接收
            printf("%c ",B->data);
            //出栈
            Go_out(s);
            if(B->rchild)
            {
                Enter(s, B->rchild);
            }
            if(B->lchild)
            {
                Enter(s, B->lchild);
            }
        }
    }
}
//中序遍历,左根右
void InOrder(BiTree L){
    BiTree B;
    stank s;
    Initie(s); //初始化栈
    if(!L){
        return;
    }
    B=L;
    while(B!=NULL || Empty(s))
    {
        while(B!=NULL)
        {
            Enter(s,B);//进栈
            B=B->lchild;//左孩子全部进栈
        }//退出循环是指针指向的左孩子为空
        B=s.arr[s.top-1];
        printf("%c ",B->data);
        Go_out(s);//出栈
        B=B->rchild;//指向右孩子
    }
}
//后序遍历
void Postorder(BiTree L){
    if(!L){
        return;
    }
    BiTree B=L;
    BiTree H=NULL;
    stank s;
    Initie(s);//初始化栈
    while(B ||Empty(s))
    {
        while(B)
        {
            Enter(s, B);
            B=B->lchild;
        }
       BiTree C=s.arr[s.top-1];
        if( C->rchild==NULL || C->rchild==H )
        {
            printf("%c ",C->data);
            Go_out(s);
            H=C;//记录当前结点
            C=NULL;
        }
        else
        {
            B=C->rchild;
        }
    }
}

int main() {
    BiTree T;
    printf("请按先序依次输入树的结点：\n");
    printf("请输入根节点：");
    T = CreeatBiTree();
    printf("前序遍历结果\n");
    Preorder(T);
    printf("\n");
    printf("中序遍历结果\n");
    InOrder(T);
    printf("\n");
    printf("后序遍历结果\n");
    Postorder(T);
    printf("\n");
    return 0;
}

运行结构如下

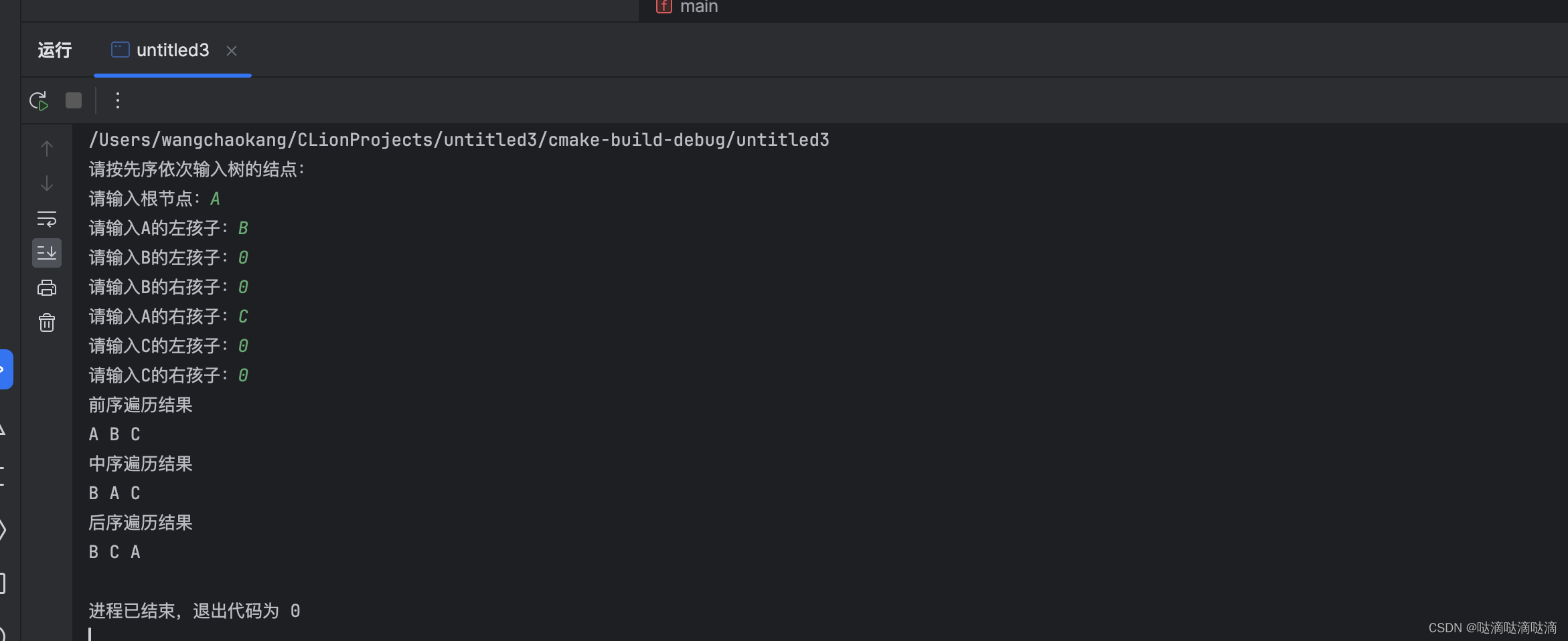
欢迎来讨论