代码随想录算法训练营第二十九天 | 39.组合总和、40.组合总和 II、131.分割回文串-优快云博客

class Solution:

    def backtracking(self, candidates, target, total, startIndex, path, result):
        if total > target:
            return
        if total == target:
            result.append(path[:])
            return

        for i in range(startIndex, len(candidates)):
            total += candidates[i]
            path.append(candidates[i])
            self.backtracking(candidates, target, total, i, path, result)  # 不用i+1了，表示可以重复读取当前的数
            total -= candidates[i]
            path.pop()

    def combinationSum(self, candidates, target):
        result = []
        self.backtracking(candidates, target, 0, 0, [], result)
        return result

40.组合总和 II

本题开始涉及到一个问题了：去重。

注意题目中给我们集合是有重复元素的，那么求出来的组合有可能重复，但题目要求不能有重复组合。

题目链接/文章讲解：代码随想录

视频讲解：回溯算法中的去重，树层去重树枝去重，你弄清楚了没？| LeetCode:40.组合总和II_哔哩哔哩_bilibili

思路

每一个元素用过就不能再用了，而且每一层里面不能取重复的数。在39题的基础上稍微修改一下就可以了。

代码

class Solution:


    def backtracking(self, candidates, target, total, startIndex, path, result):
        if total == target:
            result.append(path[:])
            return

        for i in range(startIndex, len(candidates)):
            if i > startIndex and candidates[i] == candidates[i - 1]:
                continue

            if total + candidates[i] > target:
                break

            total += candidates[i]
            path.append(candidates[i])
            self.backtracking(candidates, target, total, i + 1, path, result)
            total -= candidates[i]
            path.pop()

    def combinationSum2(self, candidates, target):
        result = []
        candidates.sort()
        self.backtracking(candidates, target, 0, 0, [], result)
        return result

131.分割回文串

本题较难，大家先看视频来理解分割问题，明天还会有一道分割问题，先打打基础。

代码随想录

视频讲解：带你学透回溯算法-分割回文串（对应力扣题目：131.分割回文串）| 回溯法精讲！_哔哩哔哩_bilibili

思路

拿着笔画一画其实可以知道大概，看图大概就可以看懂了，横向使用for循环，判断每一层切割位置，纵向是递归在当前这种切割的情况下后面的字符串的分割。

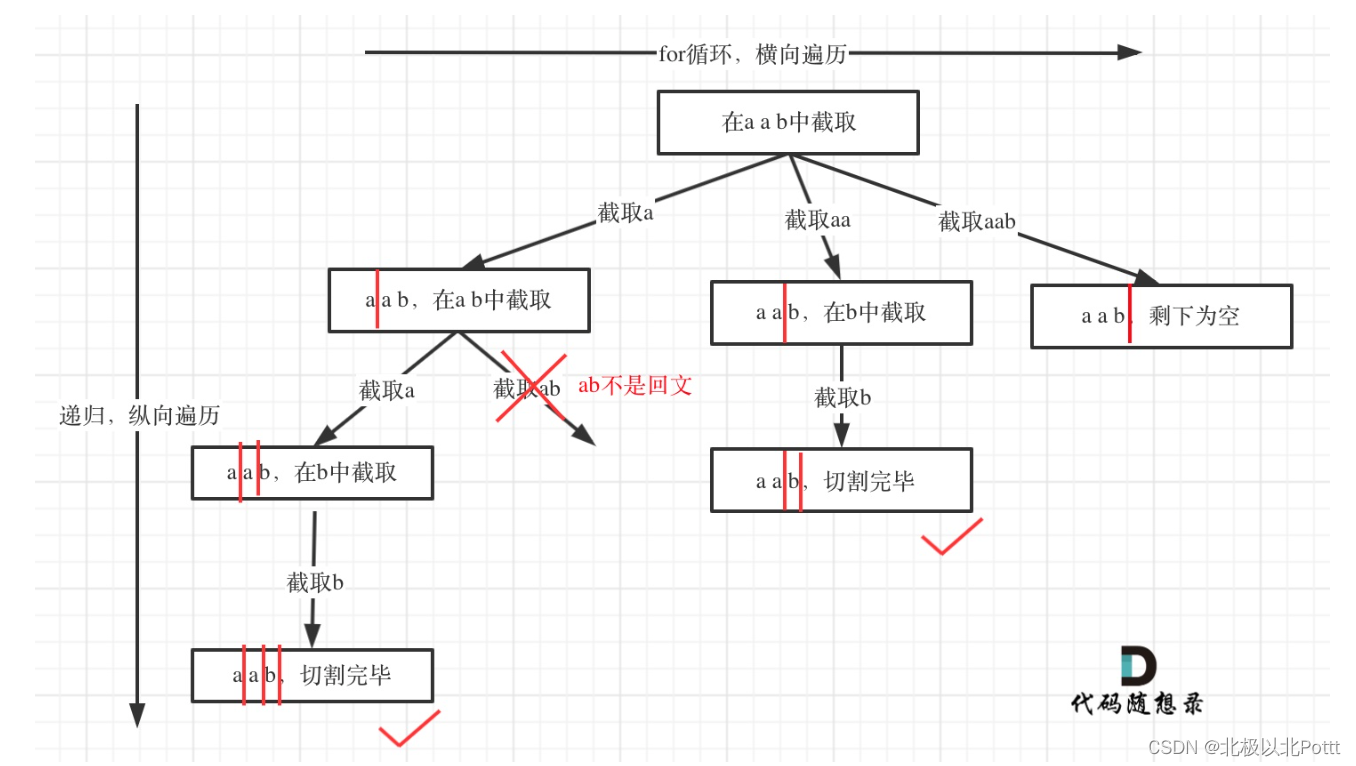
代码

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        result = []
        isPalindrome = [[False] * len(s) for _ in range(len(s))]  # 初始化isPalindrome矩阵
        self.computePalindrome(s, isPalindrome)
        self.backtracking(s, 0, [], result, isPalindrome)
        return result

    def backtracking(self, s, startIndex, path, result, isPalindrome):
        if startIndex >= len(s):
            result.append(path[:])
            return

        for i in range(startIndex, len(s)):
            if isPalindrome[startIndex][i]:   # 是回文子串
                substring = s[startIndex:i + 1]
                path.append(substring)
                self.backtracking(s, i + 1, path, result, isPalindrome)  # 寻找i+1为起始位置的子串
                path.pop()           # 回溯过程，弹出本次已经添加的子串

    def computePalindrome(self, s, isPalindrome):
        for i in range(len(s) - 1, -1, -1):  # 需要倒序计算，保证在i行时，i+1行已经计算好了
            for j in range(i, len(s)):
                if j == i:
                    isPalindrome[i][j] = True
                elif j - i == 1:
                    isPalindrome[i][j] = (s[i] == s[j])
                else:
                    isPalindrome[i][j] = (s[i] == s[j] and isPalindrome[i+1][j-1])

你知道这个任务是几号应该完成的吗，15号，你要不要看看这篇文章是什么时候发出来的。。。事情真是太多了，不扯了。每日崩溃（1/1）