CRC并行编码的纠错电路分析（计组）

​

CRC并行编码电路如图：

​

22位CRC编码，数据位16位，5位校验码，另设1位总校验码

其中的纠错电路：

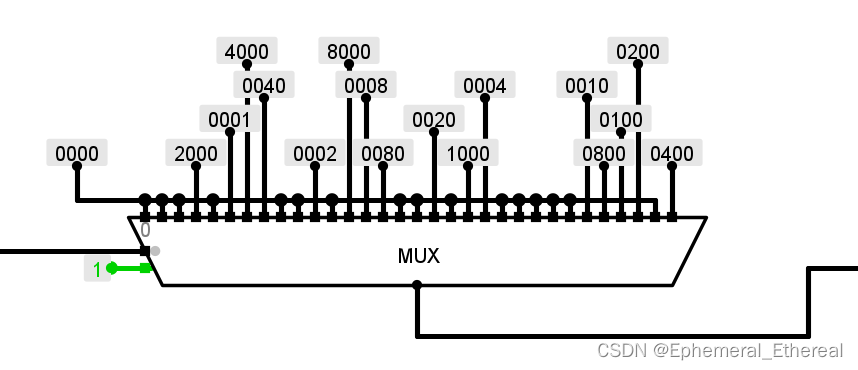
各个选择的数值是如何来的？

---

结论：一个一个算出来的

只考虑发生一位错的情况下，将每一位出错情况的余数和校验码异或，根据异或的结果输入到多路选择器中，多路选择器输出哪一位出错

① 令CRC编码的第 n 位发生错误，得到一个余数值

② 将该余数值与其他余数值、校验码（正确的余数值）异或，得到异或结果

③ 根据异或结果，选择哪一位出错（第 n 位）出错 （这一步需要人工确定选择）

事实上，观察多路选择器的所有选择，除了 0000，其余的都是只有1位是1，比如4000 H= 0100 0000 0000 0000 B，也就是说只能纠正一位错

比如，第 6 位发生错误，算出来的异或结果是 ，是多路选择器第 10 个选择，此时的选择是0002 H

也就是数据位的第2位发生了错误，可以看到第 6 位确实是数据位的第 2 位（数据范围：第 5 ~ 20 位，第 21 位即最高位设为总校验码）

计算出每一位出错的选择之后，剩下的位置就是多位错和校验码错的情况，这两种情况我们不对数据纠错，因此选择为0000

用选择器得到余数的原理

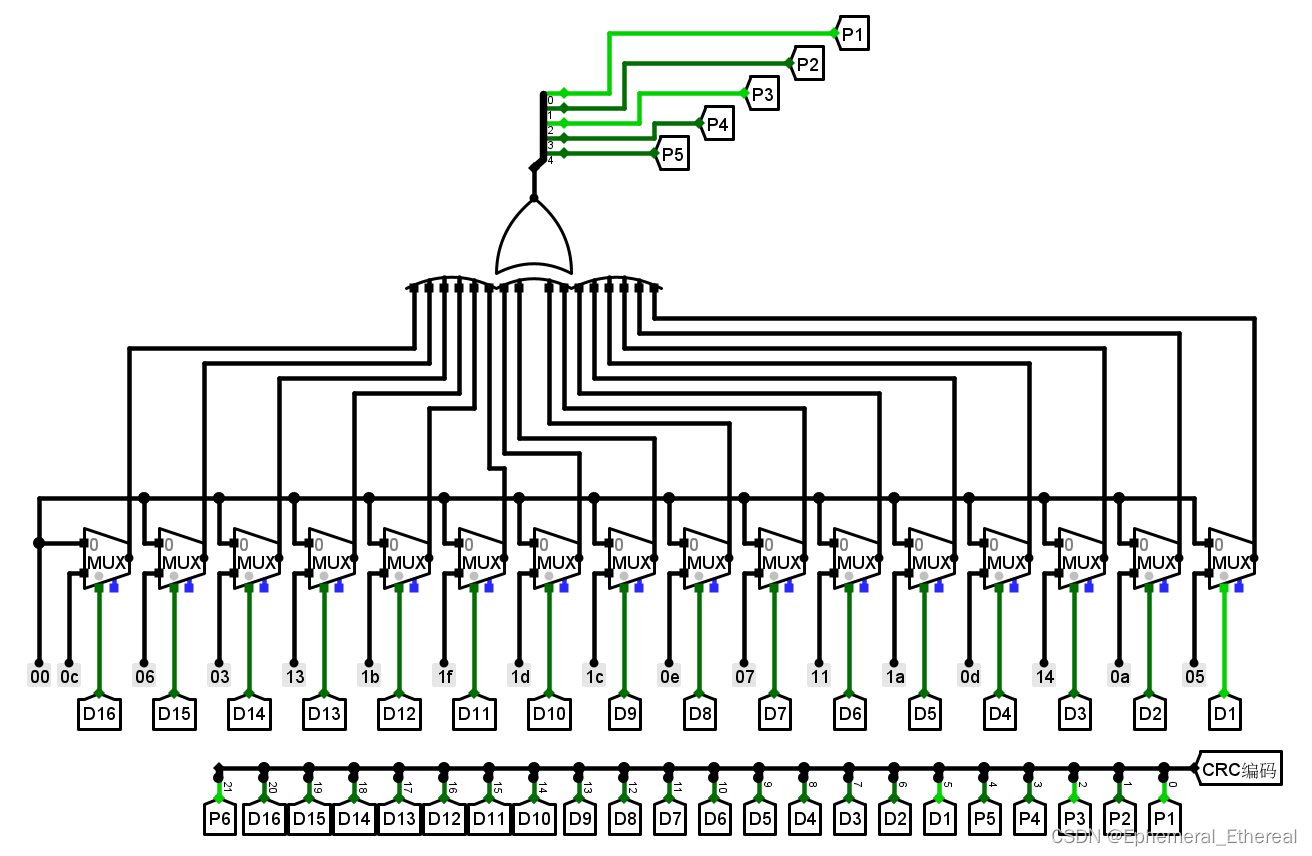
选择器的每个选择，如 0cH、06H、13H是如何算出来的？

——异或与模2除法满足结合律

放在CRC编码上看就是，将 M(x) 和生成多项式 G(x) 进行模2除法，可以先将 M(x) 划分成 ，有：

划分： ​，保持每个项只有一个1

因此选择器上面的0cH、06H、03H……是将数据（16位）划分成16份后对 G(x) 取余数的结果
根据结合律，最后的余数，也就是校验码就是每个划分的余数异或的结果，

从上图可以看到所有余数异或起来，再用分线器就得到了最终余数（校验码）