【动态规划————买股票的最佳时机含冷冻期LeedCode.309】

买股票的最佳时机含冷冻期LeedCode.309

题目网址

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。​设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
输入: prices = [1]
输出: 0

题目解析

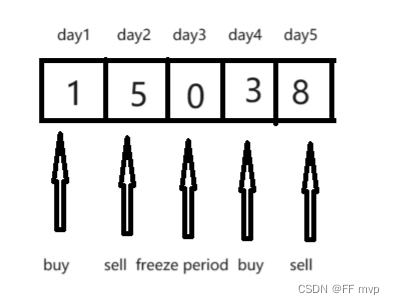
第一天买入，第二天卖出，然后第三天处于冷冻期，然后第四天买入，第五天卖出。就可以的到最大利润。因为再买股票时必须出售之前的，所以第三天不可买入。
这里我们可以采取动态规划的算法来完成。

所以我们可以创建一个二维的dp表，有prices.size()-1行，3列的dp表，第一列表示是买入操作，第二列卖出操作，第三列卖出后冷冻期操作。

dp[i][0]表示第i天买入,dp[i][1]表示第i天卖出然后冷冻期，dp[i][2]表示第i天冷冻期后

dp[i][0] = max(dp[i - 1][0],dp[i - 1][2] - prices[i]);
//买入状态，如果不能达到最大利润，可以是保持前一天的状态，如果持有保持持有，如果不持有就保持持有，等待到可以买入的状态，即冷冻期过后买入
dp[i][1] = dp[i - 1][0] + prices[i];
//卖出后状态处于冷冻期
dp[i][2] = max(dp[i - 1][2],dp[i - 1][1])
//如果是冷冻期即前一天是dp[i - 1][1]状态，如果不是冷冻期即dp[i - 1][2]状态（自身前一天状态）

初始化

第一天我们可以进行买入操作，所以dp[0][0]我们可以初始化为-prices[0]。
dp[0][1]表示卖出，因为是第一天，可以是0。

遍历顺序

因为dp表有i-1的下标，然后我们对下标为0的都进行了初始化，所以我们从第下标为1的prices的数组进行遍历。

返回值

如果在最后一天结束之后，手上仍然持有股票，那么显然是没有任何意义的。
所以我们需要在dp[n-1][1]和dp[n-1][2]取最大值

代码实现

int maxProfit(vector<int>& prices) {
    int n = prices.size();
     vector<vector<int>> dp(n,vector<int>(3));
     dp[0][0] = -prices[0];
     dp[0][1] = 0;
     dp[0][2] = 0;
     for(int i = 1;i < n;i++)
     {
         dp[i][0] = max(dp[i - 1][0],dp[i - 1][2] - prices[i]);
         //dp[i][1] = max(dp[i - 1][1],dp[i - 1][0] + prices[i]);
         dp[i][1] = dp[i - 1][0] + prices[i];
         dp[i][2] = max(dp[i - 1][2],dp[i - 1][1]);
         //dp[i][2]就是让dp[i][1]卖出后的一天不进行任何操作
     }
     return max(dp[n - 1][1],dp[n - 1][2]);
 }