人群接触网络中的SIR疫情模拟——Python实现

一、SIR模型

SIR模型是一种传播模型，是传染病模型中最经典的模型，其中S表示易感者，I表示感染者，R表示移出者。

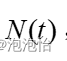设易感者的数量为,感染者的数量为移出者的数量为,总人口为,则有

 

 SIR模型的建立基于三个假设：①.人口总数不变，始终保持一个常数；②.假设t时刻单位时间内，一个病人能传染的易感者数目与此环境内易感者总数成正比，比例系数为；③.t 时刻，单位时间内从感染者中移出的人数与感染者数量成正比，比例系数为。

 用微分方程表示为：

 

def SIR(y,t,beta,gamma):
    S,I,R=y
    dSdt=-S*(I/(S+I+R))*beta
    dIdt=beta*S*I/(S+I+R)-gamma*I
    dRdt=gamma*I
    return [dSdt,dIdt,dRdt]
seed=123 #随机种子数
days=100 #模拟的天数
beta=0.30
gamma=0.10
N=150 #人群大小
I0=1 #初始感染人群
R0=0 #初始恢复人数
S0=N-I0-R0
y0=[S0,I0,R0]
from scipy.integrate import odeint
solution=odeint(SIR,y0,range(0,days),args=(beta,gamma))
import matplotlib.pyplot as plt
import pandas as pd
solution_df=pd.DataFrame(solution,columns=["S","I","R"])
color_dict={"S":"orange","I":"red","R":"green"}
solution_df.plot(figsize=(9,6),color=[color_dict.get(x) for x in solution_df.columns])

结果如图所示： 

 

 

from pyecharts.charts import Line,Grid
import pyecharts
import pyecharts.options as opts
SIR_line=Line().add_xaxis(xaxis_data=solution_df.index)
for col in solution_df.columns:
    print(col,color_dict[col])
    SIR_line.add_yaxis(series_name=col,y_axis=solution_df[col].values,
symbol_size=3, symbol='none', label_opts=opts.LabelOpts(is_show=False),
linestyle_opts=opts.LineStyleOpts(width=1.5,color=color_dict[col]),is_smooth=True)
     SIR_line.set_global_opts(axispointer_opts=opts.AxisPointerOpts(is_show=True,link=[{"xAxisIndex": "all"}]),legend_opts=opts.LegendOpts(is_show=False))
SIR_line.render_notebook()

 结果如图所示;

 

 

二、网络中的SIR模型

利用python中的network库模拟疫情传播网络，将每一个人简化为一个节点，节点的颜色代表不同的人群——黄色代表易感者、红色代表感染者、绿色代表移出者，并根据时间的推移，计算这三类人群的数量及其动态变化。

import networkx as nx
random_network=nx.barabasi_albert_graph(100,2)
nx.draw_networkx(random_network,with_labels=True,pos=nx.spring_layout(random_network,random_state=1))

 结果如图所示·：

 对网络节点和整个网络的状态进行实时更新

import random
def updateNodeState(G,node,beta,gamma):
    if G.nodes[node]["state"]=="I":
        p=random.random()
        if p<gamma:
   G.nodes[node]["state"]="R"
    elif G.nodes[node]["state"]=="S":
        p=random.random()
        k=0
        for neibor in G.adj[node]:
            if G.nodes[neibor]["state"]=="I":
                k=k+1
        if p<1-(1-beta)**k:
            G.nodes[node]["state"]="I"
def updateNetworkSate(G,beta,gamma):
    for node in G:
        updateNodeState(G,node,beta,gamma)
## 计算三类人群的数量
def countSIR(G):
    S=0
    I=0
    for node in G:
        if G.nodes[node]["state"]=="S":
            S=S+1
        elif G.nodes[node]["state"]=="I":
            I=I+1
    return S,I,len(G.nodes)-S-I

## 每个节点的颜色列表
def get_node_color(G):
    color_list=[]
    for node in G:
        color_list.append(color_dict[G.nodes[node]["state"]])
    return color_list

## 初始化网络
ba=nx.barabasi_albert_graph(N,2,seed=seed)
for node in ba:
    ba.nodes[node]["state"]="S"
ba.nodes[55]["state"]="I"

## 在days=100天期间内每天都更新网络节点状态
import time
SIR_list=[]
for t in range(0,days):
    updateNetworkSate(ba,beta,gamma)
    SIR_list.append(list(countSIR(ba)))

## 可视化网络状态变化
df=pd.DataFrame(SIR_list,columns=["S","I","R"])
df.plot(figsize=(9,6),color=[color_dict.get(x) for x in df.columns])

结果如图所示：

 对比SIR模型的结果：

solution_df.plot(figsize=(9,6),color=[color_dict.get(x) for x in df.columns])

结果如图所示：

nx.draw_networkx(ba,with_labels=True,node_color=get_node_color(ba),pos=nx.spring_layout(ba,random_state=1))

 结果如图所示：

fig,ax=plt.subplots(figsize=(15,10))
pos=nx.spring_layout(ba,random_state=1)
ax.axis("off")
plt.box(False)
nx.draw_networkx(ba,with_labels=True,font_color="white",node_color=get_node_color(ba),edge_color="#D8D8D8",pos=pos,ax=ax)

 结果如图所示：

动态展示

for node in ba:
    ba.nodes[node]["state"]="S"
ba.node[55]["state"]="I"

fig,ax=plt.subplots(figsize=(15,10))

def graph_draw(i,G,pos,ax,beta,gamma):
    ax.axis("off")
    ax.set_title("day"+str(i)+"黄色（易感者），红色（感染者），绿色（恢复者）")
    plt.box(False)
    if i==0:
        nx.draw_networkx(G,with_labels=True,font_color="white",
                         node_color=get_node_color(G),edge_color="#D8D8D8",pos=pos,ax=ax)
    else:
        updateNetworkSate(G,beta,gamma)
        nx.draw_networkx_nodes(G,with_labels=True,font_color="white",
                         node_color=get_node_color(G),pos=pos,ax=ax)
    plt.close()

import matplotlib.animation as animation
from IPython.display import HTML

plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

animator=animation.FuncAnimation(fig,graph_draw,frames=range(0,days),
                                 fargs=(ba,pos,ax,beta,gamma),interval=200)
HTML(animator.to_jshtml())

 结果如图所示：