图 (最小)生成树概念、算法思路，最短路径之dijkstra算法思路及代码

纯笔记，给自己看的

生成树

生成树：无向连通图 的极小连通子图
含n个顶点的图最多有$n^{n-2}$棵最小生成树

树型生成图:有向弱连通图？ 的极小弱连通子图

最小生成树

带权图的总权值最小的生成树

 Kruskal算法：

将边按权值排序，依次选择不会成环的权值最小的边，直到有n-1条边
 实现代码：
Q：如何判断一条边的加入是否会成环？
A：判断两点是否已经由之前的点连通
Q：如何判断判断两点是否已经由之前的点连通？
A：维护一个并查集数组

 Prim算法：

选一个点为最小生成树，找此树的所有非自己的邻接点的“距离”（权值），连最小的，将连通的顶点加入最小生成树，直到连完n个顶点
 实现代码：
Q：如何判断邻接点是不是已经在生成树里？
A：维护一个（visit之类的）标记数组
Q：如何确认最小的邻接距离（权值）
A：维护一个顶点到最小生成树的最小距离（权值）的数组（不邻接就是无穷远）,每插入一个新顶点入树，就更新对应的顶点的其他边的权值

最短路径之dijkstra算法

这个算法是单元最短路径算法，只能找到一个顶点到其他顶点的最短路径

本质上是慢慢走，在 能走的路中找最短的 ，看看能走到哪里，先走到的就算进去一个点， 是目前最近的 ，在这个基础上，重复，找下一个相对最近的点，依此类推，直到找完所有的点，这样保证最后确定的路径是最短路径

 原理：

源点到某点的最短路径，一定也是经过该路径的点对应的最短路径
找的过程中，存在“已经在最短路径上”和“只有目前所知最短路径”的两种顶点
过程中只要知道所有最短路径顶点在最短路径上的前驱，连起来，就是所有点的最短路径

 实现：

dist[N]存所有已知顶点到源点的最短路径长度
v[N]存顶点是否“已经在最短路径上”
pre[N]存各个顶点对应最短路径的前驱

代码实现:

#include<iostream>
using namespace std;
const int INF = 65535;
const int N = 110;
int 
dist[N],    //用来存“目前” start 到 i 点的最短路径
v[N],       //用来标记顶点是否纳入最短路径
pre[N],     //标记判断顶点dist的路径中，此顶点的“前驱”
g[N][N];    //图的邻接矩阵

void initGraph(int n,int m)
{
    int va=1;
    int vb=1;
    
    for (int i = 0; i < n; i++)
    {
       for (int j = 0; j < n; j++)
       {
            if(i == j)
                g[i][j] = 0;
            else
                g[i][j] = INF;
       }
    }
    for (int i = 0; i < m; i++)
    {

        cin >> va >> vb;
        cin >> g[va][vb];
        g[vb][va] = g[va][vb];
    }
}

void dijkstra(int start,int n)
{
    for (int i = 0; i < n; i++)//初始化三个标记数组
    {
        dist[i] = g[start][i];
        v[i] = 0;
        pre[i] = start;
    }
    v[start] = 1;//出发点已经纳入最短路径
    int p = start;//标记循环中，每次新纳入最短路径的顶点
    int count = 1;
    while(1)
    {
        int minW = INF;
        int pMin = -1;
        for (int i = 0; i < n; i++)//找到第一个最近顶点
        {
            if(v[i] == 0 && dist[i] < minW)
            {
                minW = dist[i];
                pMin = i;
            }
        }
        if(pMin != -1)
        {
            v[pMin] = 1;
            p = pMin;
            count++;
            if(count == n)
                return;
        }
        else
        {
            cout<<"failed , not all vex connected\n";
            return;
        }
        for (int i = 0; i < n; i++)//更新dist
        {
            if(v[i]==0 && dist[i] > dist[p] + g[p][i])
            {
                dist[i] = dist[p] + g[p][i];
                pre[i] = p;//在刷新dist的时候，（pre）前驱数组也应刷新！！！！！！！！！！！
            }
        }
    }
}

int main()
{
    int n,m;
    cin >> n >> m;
    initGraph(n,m);
    dijkstra(0,n);
    for (int i = 0; i < n; i++)
    {
        cout<< "shortest path from \'" << i << "\' to \'" << 0 << "\' =\"";
        int p = i;
        cout << p;
        while(pre[p] != p)//输出的是倒叙
        {
            p = pre[p];
            cout << p;
        }
        cout <<"\" , length = " << dist[i] << "\n";
    }
    

}

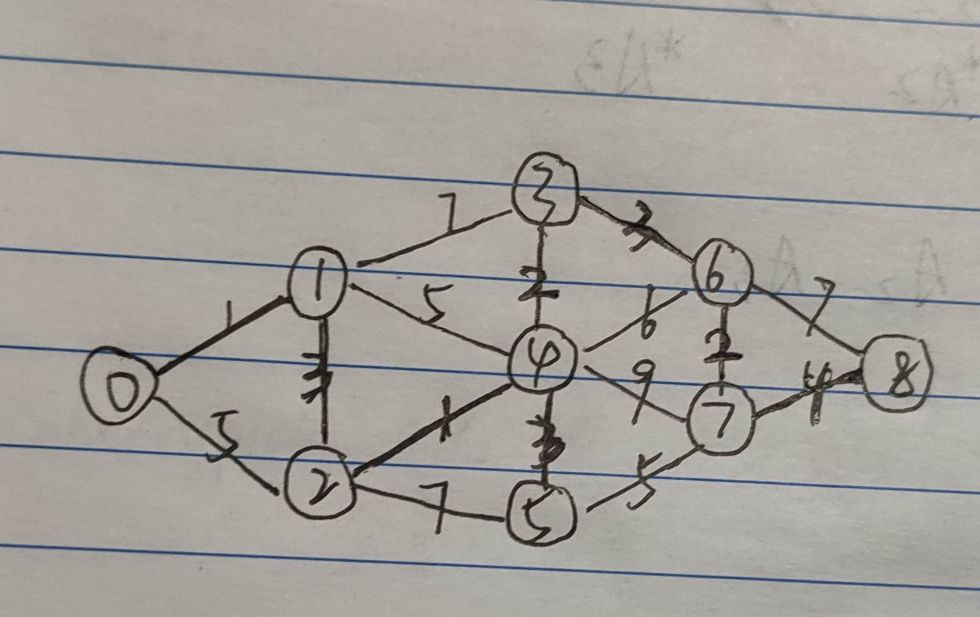
输入案例

/*
9 16
0 1 1
0 2 5
1 2 3
1 4 5
1 3 7
2 4 1
2 5 7
3 4 2
3 6 3
4 5 3
4 6 6
4 7 9
5 7 5
6 7 2
6 8 7
7 8 4
*/

输出结果

案例图示：