奈氏图与伯德图之间的关系

奈奎斯特稳定判据是通过判断奈氏图环绕（-1，0）的圈数，及环路增益（loop gain）在右平面是否有零点来判断闭环传递函数是否在右平面有极点来判断稳定性的。（ N= P- Z, where N equals the number of counterclockwise rotations of contour B about the origin; P equals the number of poles of 1 +G s H s inside contour A, and Z equals the number of zeros of 1+ G s H s inside contour A.）

先举一个绘制奈氏图的例子：

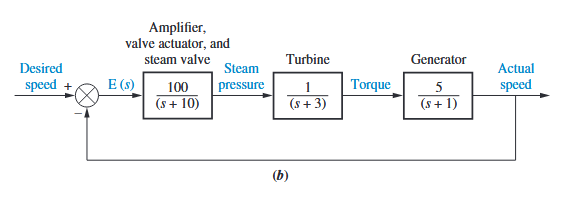
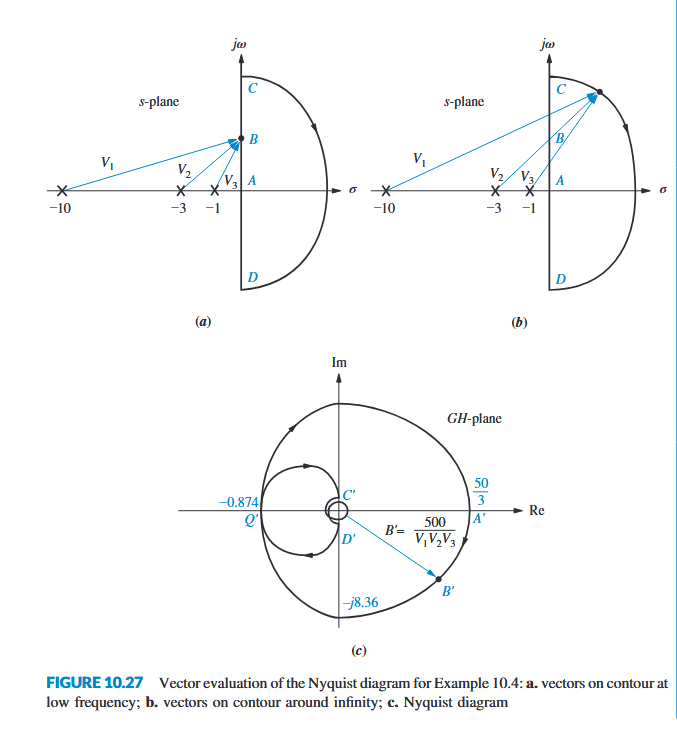
绘制从A到C的奈氏图：

绘制从C到D的图：

绘制从D到A的图：

从奈奎斯特稳定判据可以得知，我们绘制奈氏图的目的，是为了观察曲线围着（-1，0）点逆时针环绕了几圈，对于从C到D点对应的奈氏图，由于环路增益的分母的阶数比分子的阶数高很多（对于一般的系统都是这样），因此环路增益的模值应该是一个无穷小量，无论再怎么改变K,模都是在原点附近；

对于D到A的图，可以根据环路增益的实部和虚部的奇偶性直接对称得到。

因此，分析的着重点应该为对应从A到D的奈氏图，是否环绕（-1，0）点。

这一段即G(jw)，把幅值和相角分别绘制出来就是伯德图（奈氏图可以理解为一个极坐标图）。