目录
1.堆排序
首先我们了解一下什么是堆?
堆的介绍
堆是一种叫做完全二叉树的数据结构,可以分为大根堆,小根堆,而堆排序就是基于这种结构而产生的一种程序算法。
堆的分类
大根堆:每个结点的值都大于其的左孩子和右孩子节点的值。 如下图所示的是大根堆:
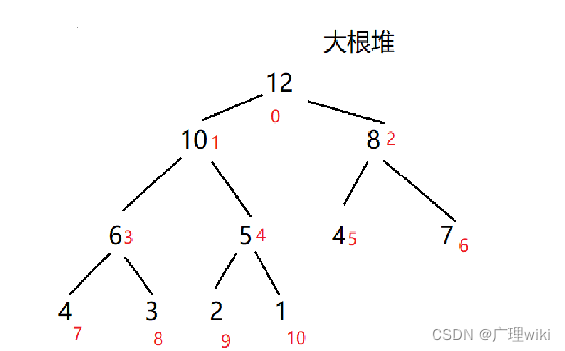
小根堆:每个结点的值都小于其左孩子和右孩子结点的值。 如下图所示的是小根堆:
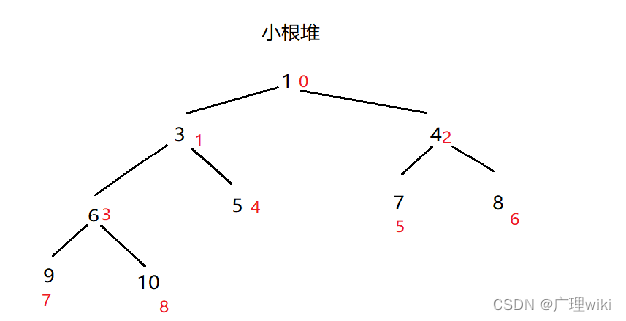
两种结构映射到数组为:
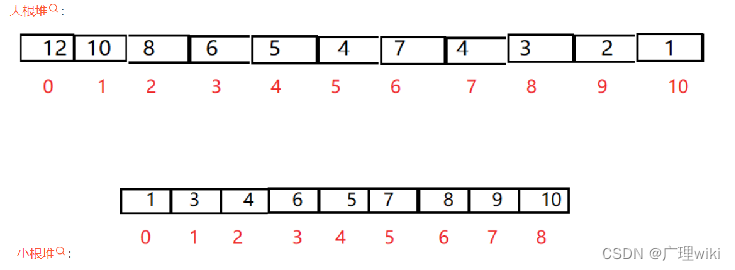
还有一个基本概念:查找数组中某个数的父结点和左右孩子结点,比如已知索引为i的数(索引就是数组的下标,这里的从0开始),那么:
1.父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
2.左孩子索引:2*i+1 3.右孩子索引:2*i+2
所以上面两个数组可以脑补成堆结构,因为他们满足堆的定义性质: 大根堆:arr(i)>arr(2*i+1) && arr(i)>arr(2*i+2) 小根堆:arr(i)<arr(2*i+1) && arr(i)<arr(2*i+2)。
排序思想:
1.首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端 。
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1 。
3.将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组 。
注意:升序用大根堆,降序就用小根堆(默认为升序)
那如何构造大根堆?

接下来就来讲一个例子来让大家更好地理解!
首先我们给定一个无序的序列,将其看做一个堆结构,一个没有规则的二叉树,将序列里的值按照从上往下,从左到右依次填充到二叉树中。
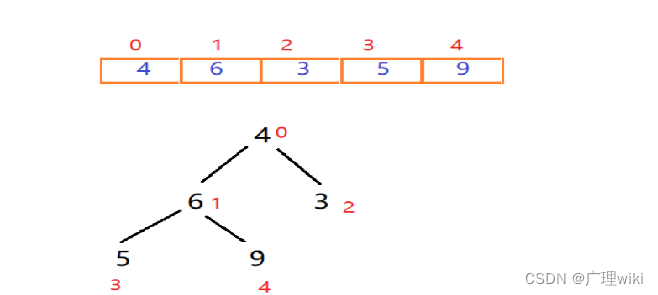
对于一个完全二叉树,在填满的情况下(非叶子节点都有两个子节点),每一层的元素个数是上一层的二倍,根节点数量是1,所以最后一层的节点数量,一定是之前所有层节点总数+1,所以,我们能找到最后一层的第一个节点的索引,即节点总数/2(根节点索引为0),这也就是第一个叶子节点,所以第一个非叶子节点的索引就是第一个叶子结点的索引-1。那么对于填不满的二叉树呢?这个计算方式仍然适用,当我们从上往下,从左往右填充二叉树的过程中,第一个叶子节点,一定是序列长度/2,所以第最后一个非叶子节点的索引就是 arr.len / 2 -1,对于此图数组长度为5,最后一个非叶子节点为5/2-1=1,即为6这个节点 那么如何构建呢? 我们找到了最后一个非叶子节点,即元素值为6的节点,比较它的左右节点中最大的一个的值,是否比他大,如果大就交换位置。
在这里5小于6,而9大于6,则交换6和9的位置,如下图所示:
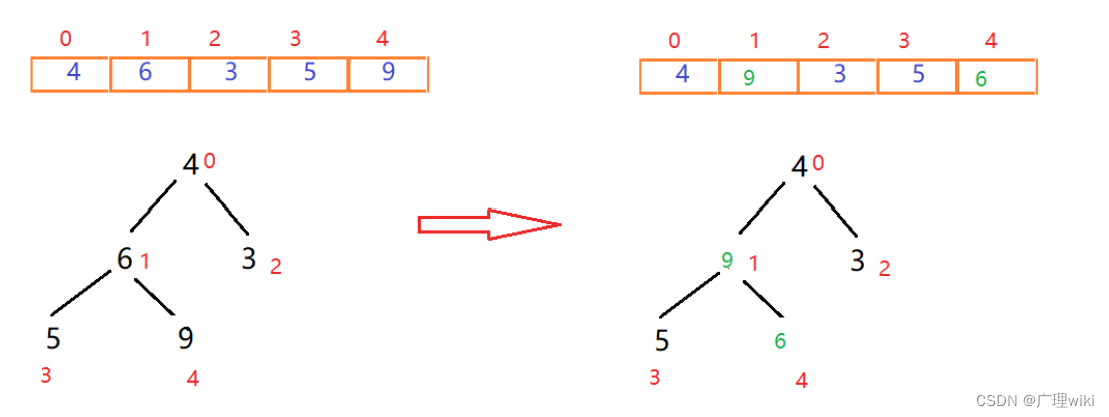
找到下一个非叶子节点4,用它和它的左右子节点进行比较,4大于3,而4小于9,交换4和9位置,如下图所示:
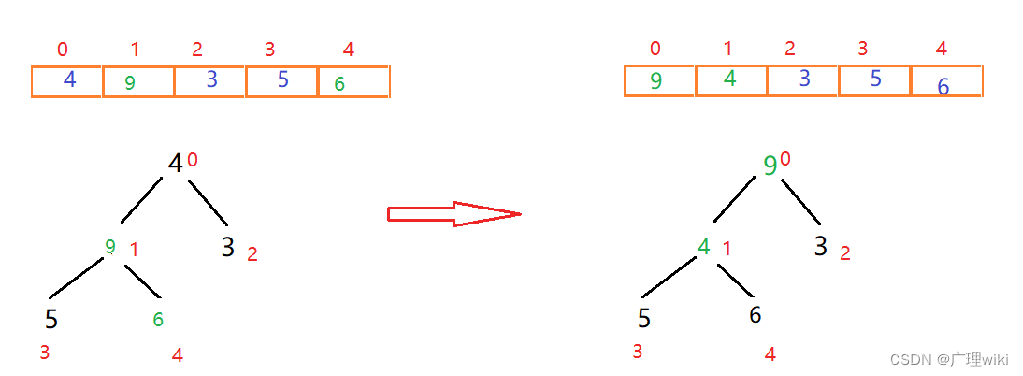
此时发现4小于5和6这两个子节点,我们需要进行调整,左右节点5和6中,6大于5且6大于父节点4,因此交换4和6的位置,如下图所示:
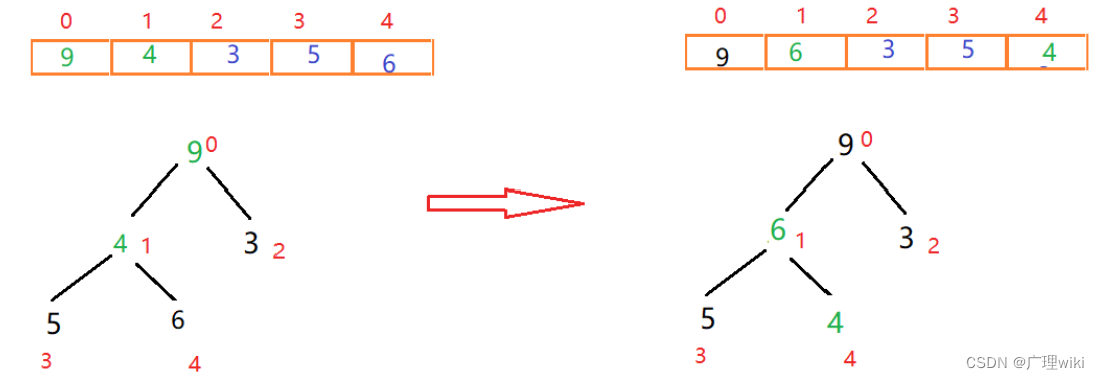
此时我们就构造出来一个大根堆,接下来进行排序:
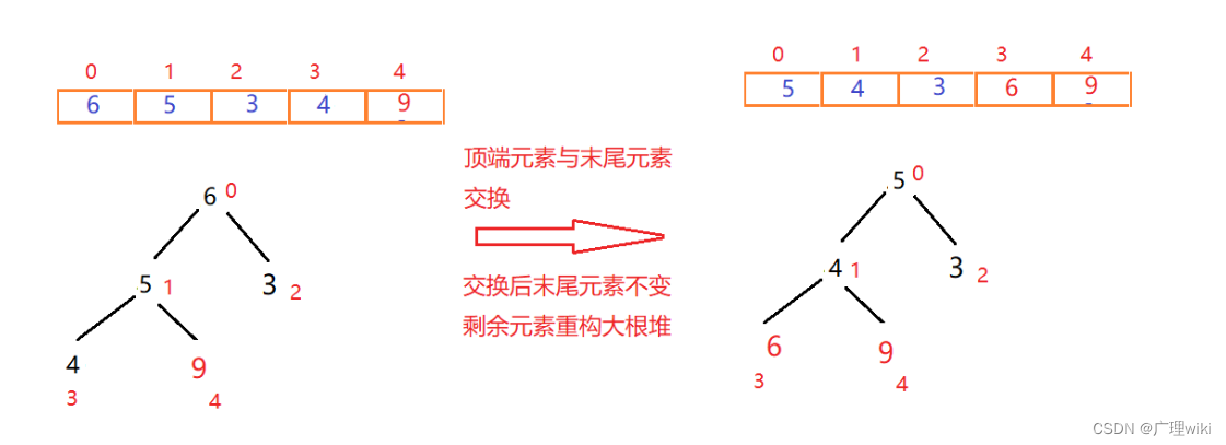
首先将顶点元素9与末尾元素4交换位置,此时末尾数字为最大值。排除已经确定的最大元素,将剩下元素按上面的方法再重新构建大根堆。 一次交换重构如图:
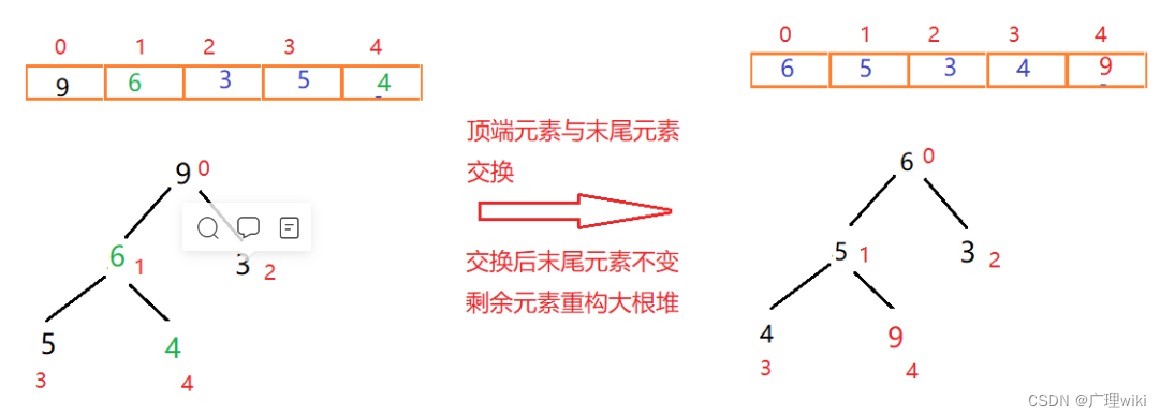
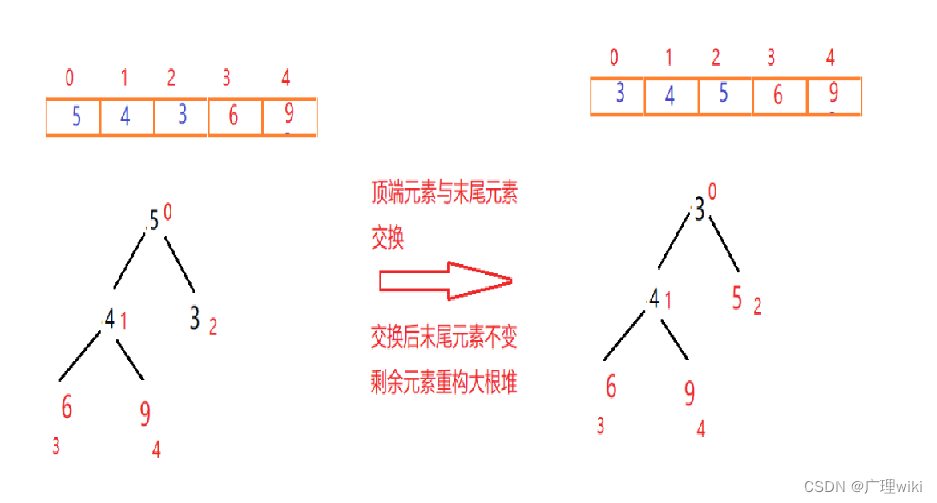
此时元素9已经有序,末尾元素则为4(每调整一次,调整后的尾部元素在下次调整重构时都不能动)。 二次交换重构如图:
最终排序结果如下图所示:
由此,我们可以归纳出堆排序算法的步骤:
1. 把无序数组构建成二叉堆。
2. 循环删除堆顶元素,移到集合尾部,调节堆产生新的堆顶。
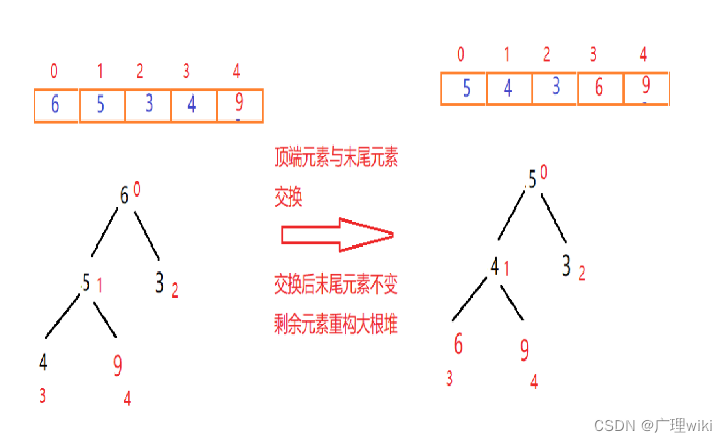
当我们删除一个最大堆的堆顶(并不是完全删除,而是替换到最后面),经过自我调节,第二大的元素就会被交换上来,成为最大堆的新堆顶。
正如下图所示,当我们删除值为9的堆顶节点,经过调节,值为6的新节点就会顶替上来;当我们删除值为6的堆顶节点,经过调节,值为5的新节点就会顶替上来.......
由于二叉堆的这个特性,我们每一次删除旧堆顶,调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶,反复调节二叉堆,所得到的集合就成为了一个有序集合, 堆排序是不稳定的排序,空间复杂度为O(1),平均的时间复杂度为O(nlogn),最坏情况下也稳定在O(nlogn) 。
void HeapAdjust(int* arr, int start, int end)
{
int tmp = arr[start];
for (int i = 2 * start + 1; i <= end; i = i * 2 + 1)
{
if (i < end&& arr[i] < arr[i + 1])//有右孩子并且左孩子小于右孩子
{
i++;
}//i一定是左右孩子的最大值
if (arr[i] > tmp)
{
arr[start] = arr[i];
start = i;
}
else
{
break;
}
}
arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{
//第一次建立大根堆,从后往前依次调整
for(int i=(len-1-1)/2;i>=0;i--)
{
HeapAdjust(arr, i, len - 1);
}
//每次将根和待排序的最后一次交换,然后在调整
int tmp;
for (int i = 0; i < len - 1; i++)
{
tmp = arr[0];
arr[0] = arr[len - 1-i];
arr[len - 1 - i] = tmp;
HeapAdjust(arr, 0, len - 1-i- 1);
}
}
int main()
{
int arr[] = { 9,5,6,3,5,3,1,0,96,66 };
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
printf("排序后为:");
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
return 0;
}2.哈(赫)夫曼树
1.路径 一个结点到另外一个结点的通路,称为路径 。(祖先结点到子孙结点)
2.路径长度: 每经过一个结点,路径长度就增加1,不包括起始结点的。
3.结点权值:对于结点赋予一个数值,表示结点的权值 比较:结点元素出现的次数。
4.带权路径长度: 从根点出发到该结点的路径长度 乘以 该结点的权值。
5.树的带权路径长度 (WPL): 树中所有叶子结点的带权路径长度之和。
6.哈夫曼树:最优二叉树,由n个叶结点组成的二叉树的带权路径长度最短。
7.结点相同,构成的哈夫曼树可能不唯一,但树的带权路径长度相等。
8.把n个结点构成哈夫曼树,这n个结点必然作为叶子结点,需要添加n-1个分支结点。
构造哈(赫)夫曼树:
遵循的原则:权重越大离根结点越近
算法描述过程:
1.把n个叶结点看作n棵独立的树,构成森林F。
2.创建一个新的结点,然后从森林F中选取两棵根结点权值最小的树作为新结点的左右子树,并且把新的结点的权值设置为这两棵树根结点权值之和。
3.从森林F中把刚才选取两棵树删除,并且把新的结点作为树的根结点加入到森林中。
4.重复2和3的步骤,直到森林中只剩下一棵树为止。
接下来就来讲讲一道例题方便大家理解吧!
例题:将题目给的这些数字构造成哈(赫)夫曼树:2,8,7,6,5。
首先对这些数字进行排序:2,5,6,7,8。
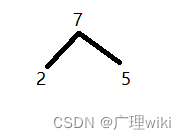
选择其中最小的两个数:2,5组成左右子树,它们的和成为子树的根结点,如下图:
构造完后将2,5从那些排好序的数字里面删除,将它们的和7加入这些数字中并重新排序:
6,7,7,8。
重新排完序后再选择其中最小的两个数:6,7组成左右子树,它们的和成为子树的根结点,如下图(两种结构):
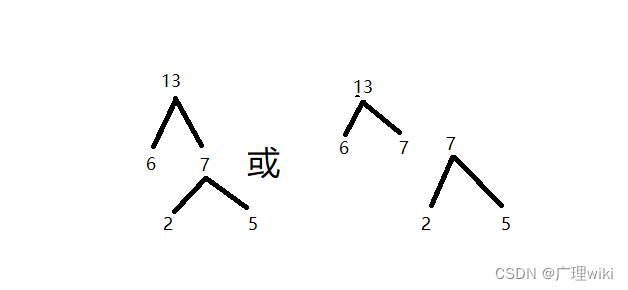
构造完后将6,7从那些排好序的数字里面删除,将它们的和13加入这些数字中并重新排序:
7,8,13。
重新排完序后再选择其中最小的两个数:7,8组成左右子树,它们的和成为子树的根结点,如下图(两种结构):
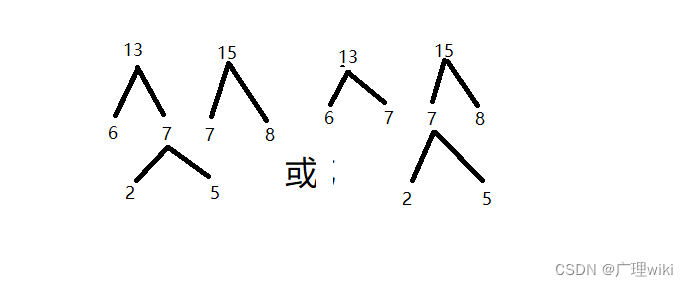
构造完后将7,8从那些排好序的数字里面删除,将它们的和15加入这些数字中并重新排序:13,15。
重新排完序后再选择其中最小的两个数:13,15组成左右子树,它们的和成为子树的根结点,如下图(两种结构),这个也是最终的结果:
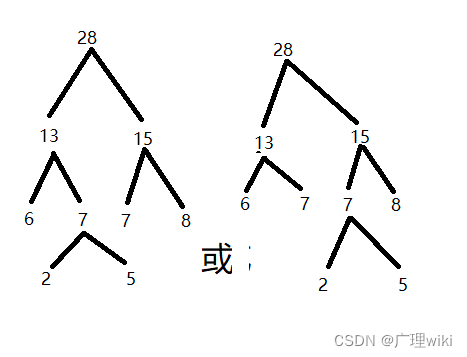
WPL=2*3+5*3+6*2+7*2+8*2=63。
最后希望大家都能够学会看懂上面这些内容,并多多关注我的文章谢谢大家!





 本文详细介绍了堆排序算法的原理和步骤,包括如何构建大根堆和进行排序,并通过实例演示了排序过程。同时,讲解了哈夫曼树的概念,包括带权路径长度、最优二叉树等,并通过示例展示了哈夫曼树的构造过程。堆排序的时间复杂度为O(nlogn),而哈夫曼树是用于优化路径长度的数据结构。
本文详细介绍了堆排序算法的原理和步骤,包括如何构建大根堆和进行排序,并通过实例演示了排序过程。同时,讲解了哈夫曼树的概念,包括带权路径长度、最优二叉树等,并通过示例展示了哈夫曼树的构造过程。堆排序的时间复杂度为O(nlogn),而哈夫曼树是用于优化路径长度的数据结构。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








