LeetCode练习数据结构（53、最大子数组和）

题目

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组 是数组中的一个连续部分。

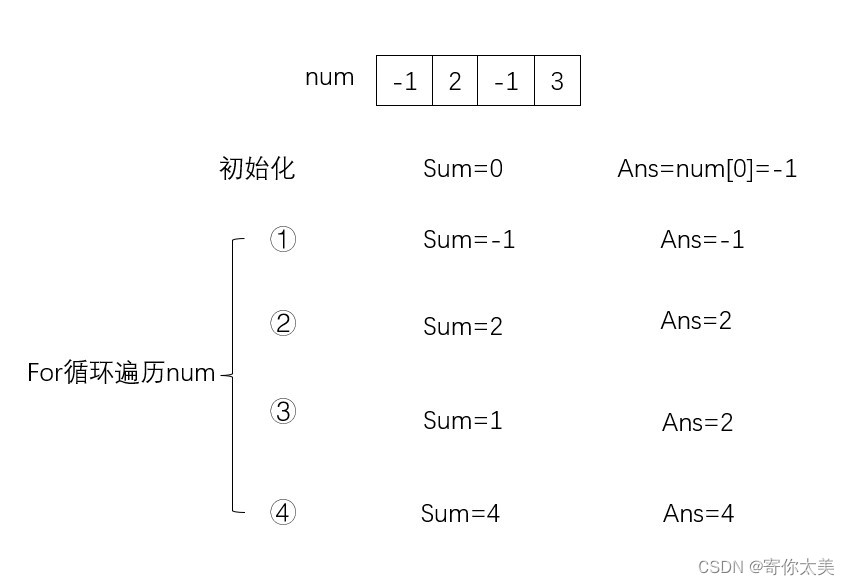
思路一 将数组从头遍历到尾

主要定义两个变量，第一个变量记录每一次加上数组中的下一个元素后和下一个元素的最大值，另一个变量记录最终结果

思路二 分治法 

子序列的结果只可能在这三部分中产生——左半部分、右半部分、中间部分，利用递归的思想不断地将数组从中间等分从而求得左半部分和右半部分中产生的子序列，而中间部分产生的子序列则是从中间开始向左右两边延伸求得的两个最大值之和

代码如下（思路一、二）

class Solution:

    #思路一
    def maxSubArray(self, nums: list[int]) -> int:
        sum=0
        ans=nums[0]
        for i in range(len(nums)):#遍历数组
            sum=max(sum+nums[i],nums[i])
            ans=max(sum,ans)#更新最终结果
        return ans


    #思路二
    #分治法
    def maxSubArray_other(self, nums: list[int]) -> int:
        count=len(nums)            #获取列表长度
        if count==1:                    #若列表中只有一个元素，则直接输出，同时也是递归的终止条件
            return nums[0]
        else:
            leftans=self.maxSubArray_other(nums[0:count//2])#递归求得左边部分的子序列最大值
            rightans=self.maxSubArray_other(nums[count//2:count])#递归求得右边部分的子序列最大值

        #若最大的子序列不再左边也不在右边，则一定在中间
        mid_left=nums[count//2-1]#左边最多可以延伸到哪里
        sum=0
        for i in range(count//2-1,-1,-1):#遍历左边求左边最大值
            sum+=nums[i]
            mid_left=max(mid_left,sum)
        sum=0
        mid_right=nums[count//2]#右边最多可以延伸到哪里
        for i in range(count//2,count,1):#遍历右边求右边最大值
            sum+=nums[i]
            mid_right=max(mid_right,sum)
        return max(leftans,rightans,mid_left+mid_right)#最大值一定在左边、右边、中间三者中产生


if __name__ == '__main__':
    s=Solution()
    nums=[-2,1,-3,4,-1,2,1,-5,4]
    print(s.maxSubArray(nums))
    print(s.maxSubArray_other(nums))

动态规划的思想是最适合的

分治法虽然也很但是如果这个题省级一下，改成求出这个子数组呢？

使用动态规划，代码如下：

不能写成>=