目录
前言
前面学习了一些关于机器学习的知识,本篇来说一说有关深度学习方面的东西——多层感知器,下面来看一些例子。
對比邏輯回歸
可以參考之前的文章:邏輯回歸

前面也说过类似问题,这里我们可以通过建立一个逻辑回归模型来实现任务,它的边界曲线大概是这样的(下图)
可以看到,边界曲线不是规则的圆或椭圆,看起来还是比较复杂的,这并不是简单的二次型能够解决的问题了,需要用到多次项来求解,这就需要我们生成多项式属性了。但如果边界曲线更复杂,初始数据属性更多,那么数据将非常庞大,运算速度就会很慢(看下一个例子)

前面我们也说过类似例子,是采用的数据降维的方法,先暂且不说这个,我们再来看一个任务
与我们人的直观判断不同,计算机看到的是一个点一个点对应的数值(灰度值)
假设有这样一张输入图片

计算机看到的是这样的

对于这样的数据计算机是如何进行二分类的?我们来简化一下

这时我们就可以通过p1、p2的灰度建立模型、给出决策边界进而求解了,如果边界是二阶的,就有右边的5项,当然高阶的项数更多,这是我们实现图片二分类问题的一个简化思路。实际上我们是要对所有的点都进行二分类的。

像400*500像素这样的一个图片,将有200000个输入数据(第一行从1到500,第二行从501到1000,以此类推)这么庞大的数据,其计算量和运行速度可想而知,所有我们需要一个更好的模型去解决该问题
多层感知器(Multi-Layer Perceptron)
簡介
多层感知器(MLP,Multilayer Perceptron)是一种前馈人工神经网络模型,其将输入的多个数据集映射到单一的输出的数据集上。

以下來自學習筆記
從邏輯回歸推導
如果学过生物的话,应该都学过人的神经元结构,其中有两个很重要的部分(树突和轴突末端)



当人看到图片时,神经元间就会进行一些信息传递进而判断出图片类别。所以当我们模仿人体神经元时,可以想象将神经元信号数值化

即是说给通过输入数据,再经过相关公式,最后生成一个新的数值信号。看到这儿,是不是感觉和逻辑回归有一些相似之处,那就再回顾一下逻辑回归模型框架

可以看到左边是我们的输入数据,中间是我们的公式,右边就是我们求得的概率了。
虽然有些相似,但人的神经元有一个不同的点就是它并不是一个单一的神经元,也可以理解成它并不是一个单一的逻辑回归结构,而是由很多个神经元组成的神经网络。那么我们能把逻辑回归组成一个网络吗?

这里我们可以这样理解,从输入神经元开始到第一个隐含神经元这样一个计算过程,是通过逻辑回归计算的,然后第一个隐含神经元和第二个隐含神经元间也是通过逻辑回归计算的(这里第一个隐含神经元的相关数据可以看作是新的输入),同理,第二个隐含神经元和输出神经元间也是通过逻辑回归计算的。
还是一样,来看一个简化的MLP模型结构

来回忆一下逻辑回归模型的一些数学公式

这里z可以是x乘以θ
那这个简化的结构的y怎么计算呢?
我们是先计算a的值然后再计算y的值(这里x0是常数项)

这里就和前面的z=xθ相同了

詳述MLP原理
前言
神经网络是当前机器学习领域普遍所应用的,例如可利用神经网络进行图像识别、语音识别等,从而将其拓展应用于自动驾驶汽车。它是一种高度并行的信息处理系统,具有很强的自适应学习能力,不依赖于研究对象的数学模型,对被控对象的的系统参数变化及外界干扰有很好的鲁棒性,能处理复杂的多输入、多输出非线性系统,神经网络要解决的基本问题是分类问题。
神经网络的变种目前有很多,如误差反向传播(Back Propagation,BP)神经网路、概率神经网络、卷积神经网络(Convolutional Neural Network ,CNN-适用于图像识别)、时间递归神经网络(Long short-term Memory Network ,LSTM-适用于语音识别)等。但最简单且原汁原味的神经网络则是多层感知器(Multi-Layer Perception ,MLP),只有理解经典的原版,才能更好的去理解功能更加强大的现代变种
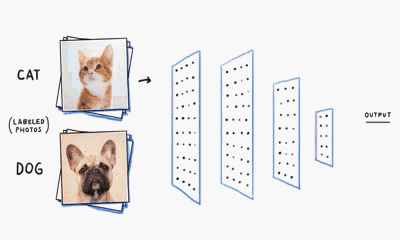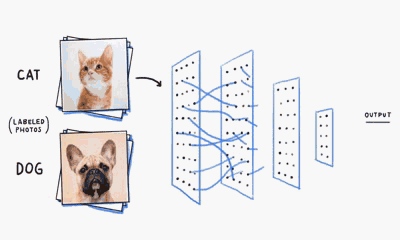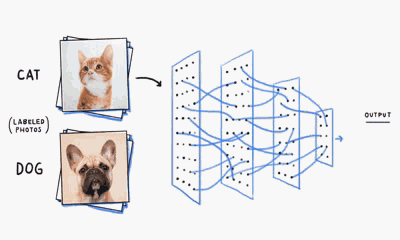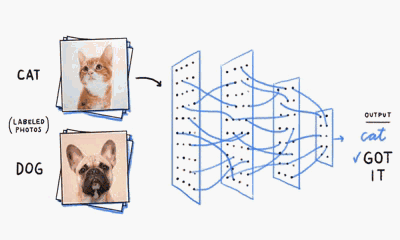
MLP神经网络的结构和原理
理解神经网络主要包括两大内容,一是神经网络的结构,其次则是神经网络的训练和学习,其就好比我们的大脑结构是怎么构成的,而基于该组成我们又是怎样去学习和识别不同事物的,这次楼主主要讲解第一部分,而训练和学习则放到后续更新中。
神经网络其实是对生物神经元的模拟和简化,生物神经元由树突、细胞体、轴突等部分组成。树突是细胞体的输入端,其接受四周的神经冲动;轴突是细胞体的输出端,其发挥传递神经冲动给其他神经元的作用,生物神经元具有兴奋和抑制两种状态,当接受的刺激高于一定阈值时,则会进入兴奋状态并将神经冲动由轴突传出,反之则没有神经冲动。

我们基于生物神经元模型可得到多层感知器MLP的基本结构,最典型的MLP包括包括三层:输入层、隐层和输出层,MLP神经网络不同层之间是全连接的(全连接的意思就是:上一层的任何一个神经元与下一层的所有神经元都有连接)。
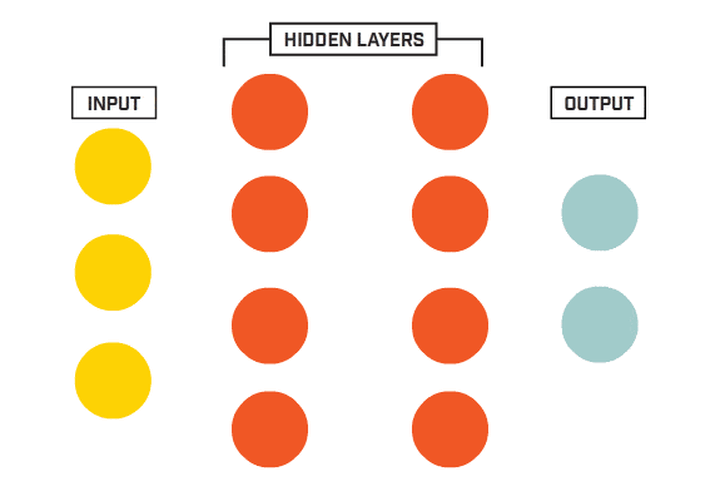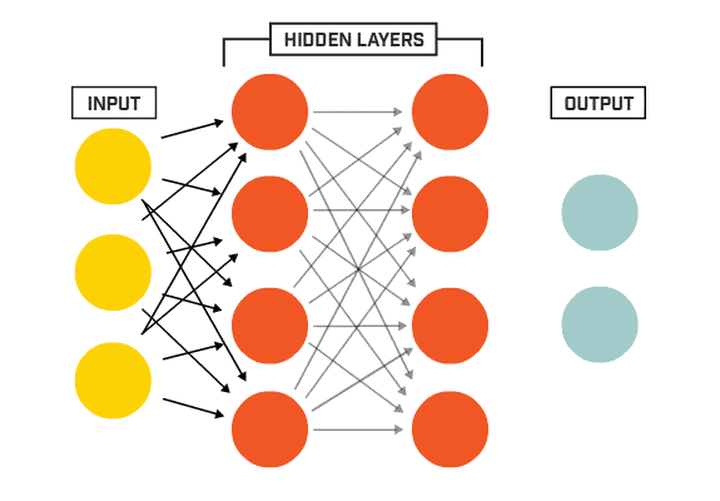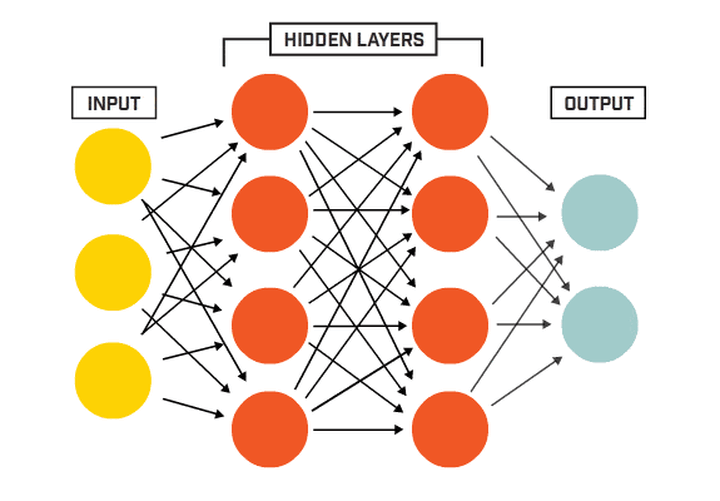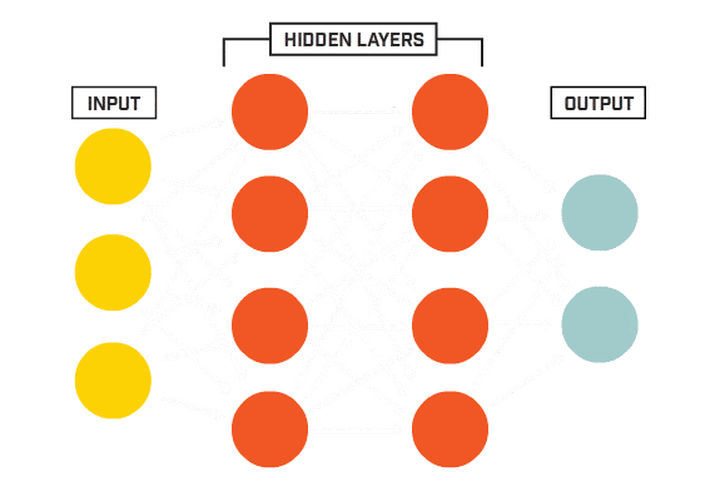

由此可知,神经网络主要有三个基本要素:权重、偏置和激活函数
-
权重:神经元之间的连接强度由权重表示,权重的大小表示可能性的大小
-
偏置:偏置的设置是为了正确分类样本,是模型中一个重要的参数,即保证通过输入算出的输出值不能随便激活。
-
激活函数:起非线性映射的作用,其可将神经元的输出幅度限制在一定范围内,一般限制在(-11)或(01)之间。最常用的激活函数是Sigmoid函数,其可将(-∞,+∞)的数映射到(0~1)的范围内。
从上图可以看到,多层感知机层与层之间是全连接的。多层感知机最底层是输入层,中间是隐藏层,最后是输出层。
隐藏层的神经元怎么得来?首先它与输入层是全连接的,假设输入层用向量X表示,则隐藏层的输出就是 f (W1X+b1),W1是权重(也叫连接系数),b1是偏置,函数f 可以是常用的sigmoid函数或者tanh函数
为嘛使用激活函数?
-
不使用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。
-
使用激活函数,能够给神经元引入非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以利用到更多的非线性模型中。
激活函数需要具备的性质
-
连续并可导(允许少数点上不可导)的非线性函数。 可导的激活函数可以直接利用数值优化的方法来学习网络参数。
-
激活函数及其导函数要尽可能的简单,有利于提高网络计算效率。
-
激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性。
sigmod 函数

导数为:



函數圖

Tanh 函数

導數

取值范围为[-1,1]
tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
与sigmod的区别是 tanh 是0 的均值,因此在实际应用中tanh会比sigmod更好。
在具体应用中,tanh函数相比于Sigmoid函数往往更具有优越性,这主要是因为Sigmoid函数在输入处于[-1,1]之间时,函数值变 化敏感,一旦接近或者超出区间就失去敏感性,处于饱和状态。
函數圖

输出层与隐藏层的关系
其实隐藏层到输出层可以看成是一个多类别的逻辑回归,也即softmax回归,所以输出层的输出就是softmax(W2X1+b2),X1表示隐藏层的输出f(W1X+b1)。
MLP整个模型就是这样子的,上面说的这个三层的MLP用公式总结起来就是,函数G是softmax。
因此,MLP所有的参数就是各个层之间的连接权重以及偏置,包括W1、b1、W2、b2。对于一个具体的问题,怎么确定这些参数?求解最佳的参数是一个最优化问题,解决最优化问题,最简单的就是梯度下降法了(SGD):首先随机初始化所有参数,然后迭代地训练,不断地计算梯度和更新参数,直到满足某个条件为止(比如误差足够小、迭代次数足够多时)。这个过程涉及到代价函数、规则化(Regularization)、学习速率(learning rate)、梯度计算等。
从上面可知下层单个神经元的值与上层所有输入之间的关系可通过如下方式表示,其它以此类推。

圖例
MLP的最经典例子就是数字识别,即我们随便给出一张上面写有数字的图片并作为输入,由它最终给出图片上的数字到底是几。
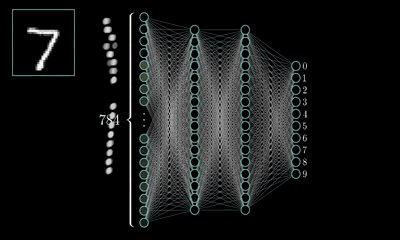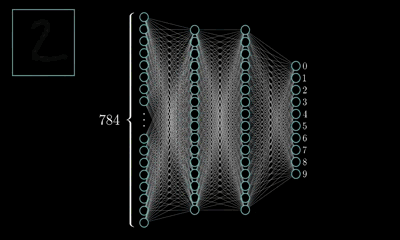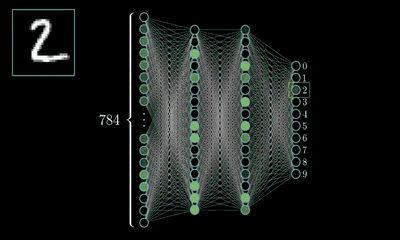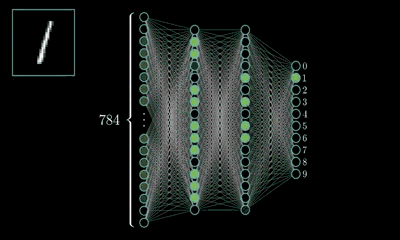
对于一张写有数字的图片,我们可将其分解为由28*28=784个像素点构成,每个像素点的值在(0~1)之间,其表示灰度值,值越大该像素点则越亮,越低则越暗,以此表达图片上的数字并将这786个像素点作为神经网络的输入。
視頻解析
而输出则由十个神经元构成,分别表示(09)这十个数字,这十个神经元的值也是在(01)之间,也表示灰度值,但神经元值越大表示从输入经判断后是该数字的可能性越大。
視頻解析
隐层的层数和神经元的选择需根据具体情况选择,此例选择两层隐层,每层16个神经元。那么根据上面的叙述,根据权重、偏置的个数此神经网络将会有13002个参数需要去调节,而如何调整这些参数,从而使神经网络有较好的学习效果则正是下篇更新的神经网络训练和学习的内容。
視頻解析
通过上面的叙述,该图像识别问题最终可通过线性方程的方式表示出来,从而来描述本篇通过MLP神经网络进行数字识别的案例,并通过建立的问题描述模型来编程实现。
視頻解析
實戰
好壞質檢二分類mlp實戰
基於data.csv數據,建立mlp模型,計算其在測試數據上的準確率,可視化模型預測結果:
- 進行數據分離: test_size=0.33,random_state=10
- 模型結構: 一層隱藏層, 有20個神經元
加載數據
#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('mlp_data.csv')
data.head()
定義X和y
#define the X and y
X = data.drop(['y'],axis=1)
y = data.loc[:,'y']
X.head()

可視化看一下
#visualize the data
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(5,5))
passed = plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1])
failed = plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0])
plt.legend((passed,failed),('passed','failed'))
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('raw data')
plt.show()

使用sklearn劃分測試集和訓練集
#split the data
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.33, random_state=10)
print(X_train.shape, X_test.shape, X.shape)
test_size為測試集比例,從維度可以看出訓練集占67%,測試集占33%

加載keras的順序模型添加各層網絡
#set up the model
from keras.models import Sequential
from keras.layers import Dense,Activation
mlp = Sequential()
mlp.add(Dense(units=20, input_dim=2, activation='sigmoid')) # units:隱藏層有20個神經元,input_dim:一開始輸入維度有x1 x2兩個
mlp.add(Dense(units=1, activation='sigmoid'))
mlp.summary()
mlp.summary():看模型結構

可以看出只有一個隱藏層,隱藏層神經元數量為20,訓練參數有60個;一個二分類任務輸出層當然只有一個神經元了;一共訓練參數有81個,從這也可以大概感覺出mlp模型訓練參數會特別多特別慢
配置模型
#compile the model
mlp.compile(optimizer='adam',loss='binary_crossentropy') # optimizer:優化方法, loss:損失函數
訓練模型
#train the model
mlp.fit(X_train,y_train,epochs=3000) # 可以發現損失函數越來越小
先迭代3000次試試看,後面可以看出效果一般,而且很耗時

make prediction and calculate the accuracy
#make prediction and calculate the accuracy
# y_train_predict = mlp.predict_classes(X_train) # Tensorflow 2.6 版本,删除了predict_classes() 这个函数,2.6以上會報錯
# Tensorflow 2.6以上版本,網上大部分說使用這個辦法,但是我發現這樣概率很低不知道是什麽原因
# y_train_predict = mlp.predict(X_train)
# print(y_train_predict)
# y_train_predict=np.argmax(y_train_predict,axis=1)
# print(y_train_predict)
# 使用以下辦法np.around(mlp.predict())取代predict_classes()好像概率正常點
y_train_predict = np.around(mlp.predict(X_train))
from sklearn.metrics import accuracy_score
accuracy_train = accuracy_score(y_train,y_train_predict)
print(accuracy_train)
從下圖可以看出準確率有91%,也還可以了

根据测试数据进行预测
#make prediction based on the test data
y_test_predict = np.around(mlp.predict(X_test))
accuracy_test = accuracy_score(y_test,y_test_predict)
print(accuracy_test)
测试数据準確率也有91%,看來沒有過擬合

print(y_train_predict)
y_train_predict_form = pd.Series(i[0] for i in y_train_predict)
print(y_train_predict_form)

生成绘图的新数据
# generate new data for plot
xx, yy = np.meshgrid(np.arange(0,1,0.01), np.arange(0,1,0.01))
x_range = np.c_[xx.ravel(), yy.ravel()]
y_range_predict = np.around(mlp.predict(x_range))
print(type(y_range_predict))
格式化
# format the output
y_range_predict_form = pd.Series(i[0] for i in y_range_predict)
print(y_range_predict_form)
fig2 = plt.figure(figsize=(5,5))
passed_predict = plt.scatter(x_range[:,0][y_range_predict_form==1],x_range[:,1][y_range_predict_form==1])
failed_predict = plt.scatter(x_range[:,0][y_range_predict_form==0],x_range[:,1][y_range_predict_form==0])
passed = plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1])
failed = plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0])
plt.legend((passed,failed,passed_predict,failed_predict),('passed','failed','passed_predict','failed_predict'))
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('raw data')
plt.show()
可視化看一下
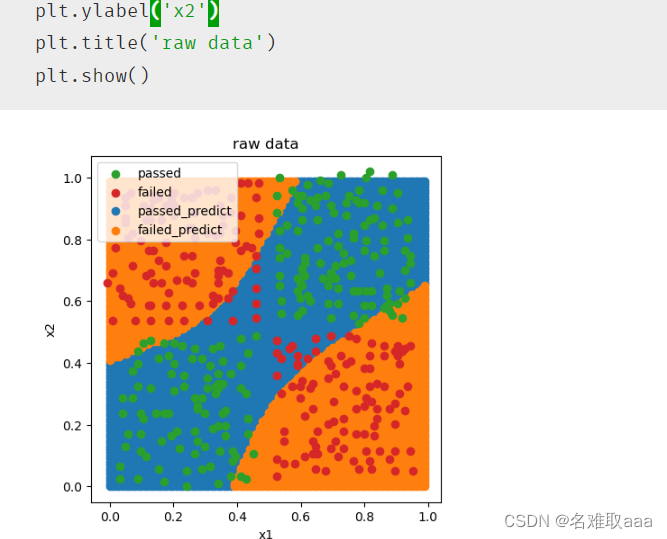
可以看出效果還不錯
再訓練3000次試試看效果

對比上面的損失函數好像沒有差別

不過看一下準確率99%倒是提高不少了
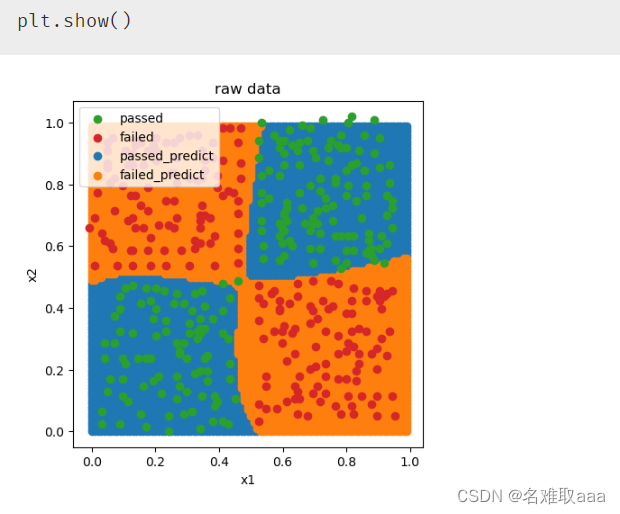
再可視化看一下,可以看出迭代6000次效果就很不錯了,只有一個點沒預測到,但是耗很多時間
總結
好壞質檢二分類mlp實戰summary:
- 通過mlp模型,在不增加特徵項的情況下,實現了非綫性二分類任務
- 掌握了mlp模型的建立、配置與訓練方法,並實現基於新數據的預測
- 熟悉了mlp分類的預測數據格式,並實現格式轉換
- 核心算法參考鏈接:https://keras-cn.readthedocs.io/en/latest/#30skeras
這就是本次學習深度學習之多層感知器(MLP)的筆記
附上本次實戰的數據集和源碼:
鏈接:https://github.com/fbozhang/python/tree/master/jupyter








 本文介绍了多层感知器(MLP)的基本概念,从逻辑回归出发解释了神经网络的构建,强调了激活函数的重要性,并探讨了Sigmoid和Tanh函数。通过实例展示了MLP在二分类问题中的应用,包括模型结构、训练过程和性能评估。
本文介绍了多层感知器(MLP)的基本概念,从逻辑回归出发解释了神经网络的构建,强调了激活函数的重要性,并探讨了Sigmoid和Tanh函数。通过实例展示了MLP在二分类问题中的应用,包括模型结构、训练过程和性能评估。

















 4871
4871

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








