代码随想录算法训练营第27天｜leetcode455.分发饼干、leetcode376.摆动序列、leetcode53.最大子序和

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。常识性推导加上举反例

1.455. 分发饼干 - 力扣（LeetCode）

不赘述，思路很简单了。但是我下面写复杂了....这么简单的题写的这么复杂...没有保持循环不变量。饼干和胃口同时变了，得固定一个。。。

    int findContentChildren(vector<int> &g, vector<int> &s)
    {
        sort(g.begin(), g.end()); // 胃口从小到大
        sort(s.begin(), s.end()); // 饼干从小到大
        int result = 0;
        int idx = 0;
        for (int i = 0; i < g.size(); i++)
        {
            while(idx<s.size()&&s[idx]<g[i]){
                idx++;
            }
            if (idx < s.size() && s[idx] >= g[i])
            {
                result++;
                idx++;
                continue;
            }
            else
            {
                break;
            }
        }
        return result;
    }

所以下面固定了胃口，用饼干去循环，如果s[i]>=g[idx]，再移动到下一个孩子的胃口。

    int findContentChildren(vector<int> &g, vector<int> &s)
    {
        sort(g.begin(), g.end()); // 胃口从小到大
        sort(s.begin(), s.end()); // 饼干从小到大
        int result = 0;
        int idx = 0;
        for (int i = 0; i < s.size(); i++)
        {
            if (idx < g.size() && s[i] >= g[idx])
            {
                result++;
                idx++;
            }
        }
        return result;
    }

2.376. 摆动序列 - 力扣（LeetCode）

贪心算法
考虑三种情况：上下坡有平坡；数组收尾两端；单调平坡有平坡

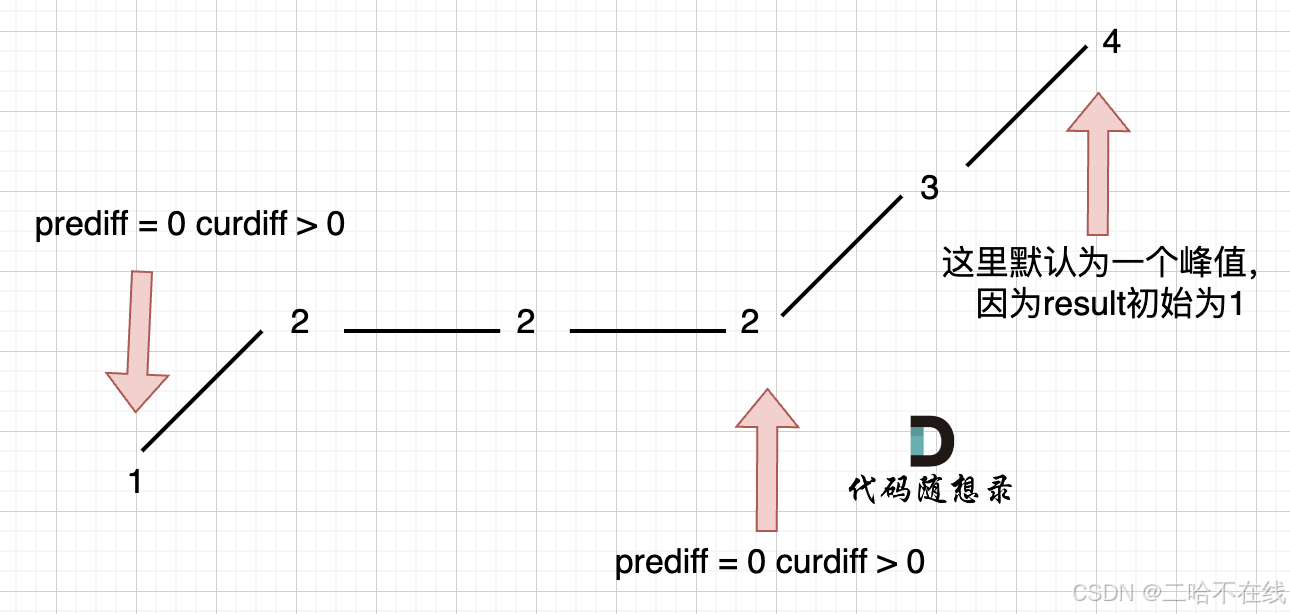
 int wiggleMaxLength(vector<int> &nums)
    {
        if (nums.size() <= 1)
            return nums.size();
        int curdiff = 0; // 当前差值
        int prediff = 0; // 前一个差值
        int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值
        for (int i = 0; i < nums.size() - 1; i++)
        {
            curdiff = nums[i + 1] - nums[i];
            if (prediff <= 0 && curdiff > 0 || prediff >= 0 && curdiff < 0)
            {//扣住极值点条件！！！
                result++;
                prediff = curdiff;
            }   
        }
        return result;
    }

3.53. 最大子数组和 - 力扣（LeetCode）

思路1：贪心算法，
sum = max(nums[1]，nums[i]+sum);           res = max(res,sum);
比如说 1 -2  3. 3比-1大的话，sum直接就🟰3.然后每次这个局部最优的sum与全局的res去比较。逐步的从局部最优转向全局最优

    int maxSubArray(vector<int> &nums)
    {
        if (nums.size() <= 1)
            return nums[0];
        int res = INT32_MIN;
        int sum = 0;
        for (int i = 0; i < nums.size(); i++)
        {
            sum = max(nums[i], nums[i] + sum);
            res = max(res, sum);
        }
        return res;
    }