文章介绍了位图在海量数据存储中的应用，通过位运算高效判断元素是否存在，同时讨论了布隆过滤器的概念、实现以及误判概率，重点讲解了如何选择哈希函数数量和位图长度以优化性能。
目录
一、位图
1.1 位图概念
我们先来看一个问题：
给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在 这40亿个数中。
我们先来考虑两种解决方案：
- set
- 排序+二分查找
但是这里是40亿个整数，1个整数4个字节，那么它总共就需要160亿个字节1G=1024MB=1024*1024KB=1024*1024*1024B（2^30B） ，这样计算下来就需要大概16G的内存，如果用set那么消耗的空间就更大了，因为它底层是红黑树，牵扯到的数据更加多了。
那应该怎么办呢？
这就需要用到位图了，题目中的要求是只判断在不在，那么我们就可以用二进制的比特位来表示数据是否存在的信息了，如1代表存在，0代表不存在。
所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用 来判断某个数据存不存在的。
因此对于这道题，我们先开2^32个比特位，即2^29个字节，上面写出1G是2^30个字节，这里只需要0.5G的空间。
1.2 位图的实现
那我们要如何具体实现？这里的问题在于就代码而言我们无法实现直接对比特位进行操作，假设我们开的是一个存放int数据的vector，我们需要控制的是比特位，但实际操作的是整型，因此我们要把握的是在int数据中找到对应的比特位。 
如图，每一个int类型的数据有4个字节，即32个比特位，那么对于给定的数 x ，我们将 x/32就可以知道它是在第几个整型上，那么它在整型的第几个比特位呢？我们只需将 x%32 即可。
找到位置，我们就要用位运算对其做置0或置1的操作了。
先来看置1：
假设我们要把红色的位置（记作 j ）置1，那么只需要一个新的全0空间（只有对应位置是1），然后对它们进行或操作。这要就能保证其他位不变，目标位置1。如何创造这样的空间呢？只需要将1<< j 个单位就可以啦。
//将存在的位置置1
void set(size_t x)
{
//第几个整型上
size_t i = x / 32;
//整型的第几个比特位上
size_t j = x % 32;
_a[i] |= 1 << j;
}对于置0：
要置0，只需要如图操作，将二者&一下即可，那么如何获取下面的空间呢?只需要置1中的这种空间取反就可以了。要注意是按位取反~
//将不存在的位置置0
void reset(size_t x)
{
//第几个整型上
size_t i = x / 32;
//整型的第几个比特位上
size_t j = x % 32;
_a[i] |= ~(1 << j);
}bool Test(size_t x)
{
size_t i = x / 32;
size_t j = x % 32;
return _a[i] & (1 << j);
}这里的设计也很巧妙，可以仔细思考一下。
整体代码：
namespace lee
{
template<size_t N>
class bitset
{
public:
bitset()
{
//除完向上取整
_a.resize(N / 32 + 1);
}
//将存在的位置置1
void set(size_t x)
{
//第几个整型上
size_t i = x / 32;
//整型的第几个比特位上
size_t j = x % 32;
_a[i] |= 1 << j;
}
//将不存在的位置置0
void reset(size_t x)
{
//第几个整型上
size_t i = x / 32;
//整型的第几个比特位上
size_t j = x % 32;
_a[i] |= ~(1 << j);
}
bool Test(size_t x)
{
size_t i = x / 32;
size_t j = x % 32;
return _a[i] & (1 << j);
}
private:
vector<int> _a;
};
}
那么对于开头的问题，我们要开多大的空间呢？
我们需要开42亿字节的空间，虽然题目里只有40亿个无符号整数，但是他们的数值可能会大于40亿。
有以下三种开辟的方法：
lee::bitset<UINT32_MAX> bs;
lee::bitset<-1> bs;
lee::bitset<0xffffffff> bs;1、3种就不用解释了，第2种是因为-1在遇到size_t（无符号）时，会发生类型转换，最后是补码全1。
1.3 位图应用
1.3.1
我们再来看一道问题：给定100亿个整数，设计算法找到只出现一次的整数。
如果想用哈希表统计次数，也是不行的。这里不妨想想用两个位来表示，两个位可以表示4种状态：00、01、10、11，在这里我们甚至只需用到前三个：00（没有出现）、01（出现一次）。10（出现两次及以上）
我们可以将原先的位图中32位分成16位，2为表示一种状态，还可以用两个原先的位图来达到目的：
class twobitset
{
public:
void set(size_t x)
{
// 00->01
if (!_bs1.test(x) && !_bs2.test(x))
{
_bs2.set(x);
}
// 01->10
else if (!_bs1.test(x) && _bs2.test(x))
{
_bs1.set(x);
_bs2.reset(x);
}
}
bool is_once(size_t x)
{
// 01为出现一次
return !_bs1.test(x) && _bs2.test(x);
}
private:
bitset<N> _bs1;
bitset<N> _bs2;
};1.3.2
给两个文件，分别有100亿个整数，但只有1G内存，如何找到这两个文件的交集？
可以分别先把100亿个整数是否存在的结果放入两个位图中，这样对于重复的数字也能达到去重的效果，如果两个位图的同一位置都存在，那么这个位置就是两个文件的交集。
int a1[] = { 1,2,3,3,4,4,4,4,4,2,3,6,3,1,5,5,8,9 };
int a2[] = { 8,4,8,4,1,1,1,1 };
lee::bitset<10> bs1;
lee::bitset<10> bs2;
// 去重
for (auto e : a1)
{
bs1.set(e);
}
// 去重
for (auto e : a2)
{
bs2.set(e);
}
for (int i = 0; i < 10; i++)
{
if (bs1.test(i) && bs2.test(i))
{
cout << i << " ";
}
}
cout << endl;二、布隆过滤器
上述问题我们解决的问题都是利用整型来完成的，假如我们要存的是字符串呢？
那么我们就需要将字符串映射到位图当中，即将字符串转为整型，再放入位图：
但是这样的方式存在一个致命的问题：不同的字符串可能会对应到相同的整型，这便会引发冲突： 对于在的元素可能存在误判，但是不存在的元素是肯定不存在的。
而通过一定的方式是可以减少误判概率的，就是接下来要学习的布隆过滤器。
2.1 布隆过滤器的概念
布隆过滤器是由布隆在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你“某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间
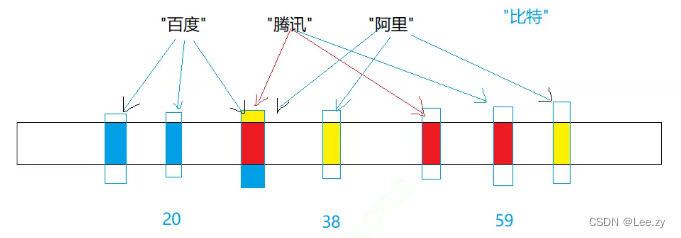
如图，一个字符串映射到多个位置，如果每个位置都为1，才会引发冲突，这样就降低了误判率但不是完全消除误判。
2.2 布隆过滤器的实现
class BloomFilter
{
public:
void Set(const K& key)
{
size_t hash1 = Hash1()(key) % N;
_bs.set(hash1);
size_t hash2 = Hash2()(key) % N;
_bs.set(hash2);
size_t hash3 = Hash3()(key) % N;
_bs.set(hash3);
/* cout << hash1 << endl;
cout << hash2 << endl;
cout << hash3 << endl << endl;*/
}
bool Test(const K& key)
{
//只要有一个位置不存在就返回false
size_t hash1 = Hash1()(key) % N;
if (_bs.test(hash1) == false)
return false;
size_t hash2 = Hash2()(key) % N;
if (_bs.test(hash2) == false)
return false;
size_t hash3 = Hash3()(key) % N;
if (_bs.test(hash3) == false)
return false;
return true;
}
private:
bitset<N> _bs;
};2.3 布隆过滤器的删除
布隆过滤器是不支持删除操作的，因为一个数据的删除可能会影响其他数据。
一种支持删除的方法：将布隆过滤器中的每个比特位扩展成一个小的计数器，插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一，删除元素时，给k个计数器减一，通过多占用几倍存储空间的代价来增加删除操作。
2.4 如何选择哈希函数个数和布隆过滤器的长度
通过查阅资料发现，哈希函数越多，误判率会越低。
我们可以根据这个公式来选择合适的k和m。
扫一扫
1187
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
