卷积神经网络

目录

一、引入卷积神经网络原因

二、网络结构

2.1 卷积层正向传播过程

2.1.1 卷积

数学公式表示

2.1.2 填充（Padding）

2.1.3 步幅（stride）

2.1.4 输出特征图的尺寸计算公式

2.1.5 卷积参数共享

2.1.6 多层卷积核

2.1.6 感受野

2.2 池化层正向传播过程

池化（Pooling） 操作

池化好处

2.2 全连接层正向传播过程

三、训练算法

3.1 卷积层反向传播算法

3.2 池化层反向传播算法

平均池化

最大池化

四、残差连接

五、卷积神经网络实现手写数字识别代码

4.1 代码分块

1）数据处理

2）模型设计

3）训练模型

4）保存模型

5）测试模型

4.2 完整代码 

---

一、引入卷积神经网络原因

手写数字识别任务中使用全连接网络进行特征提取， 将一张图片上的所有像素点展开成一个 1 维向量输入网络， 这种方式存在如下两个问题：

• 模型参数过多， 容易发生过拟合。 在全连接前馈网络中， 隐藏层的每个神经元都要跟该层所有输入的神经元相连接。 随着隐藏层神经元数量的增多，参数的规模也会急剧增加， 导致整个神经网络的训练效率非常低， 也很容易发生过拟合。
• 难以提取图像中的局部不变性特征。 自然图像中的物体都具有局部不变性特征， 比如尺度缩放、 平移、 旋转等操作不影响其语义信息。 而全连接前馈网络很难提取这些局部不变性特征。

为了解决上述问题， 引入了卷积神经网络进行特征提取， 既能提取到相邻像素点之间的特征模式， 又能保证参数的个数不随图片尺寸变化。

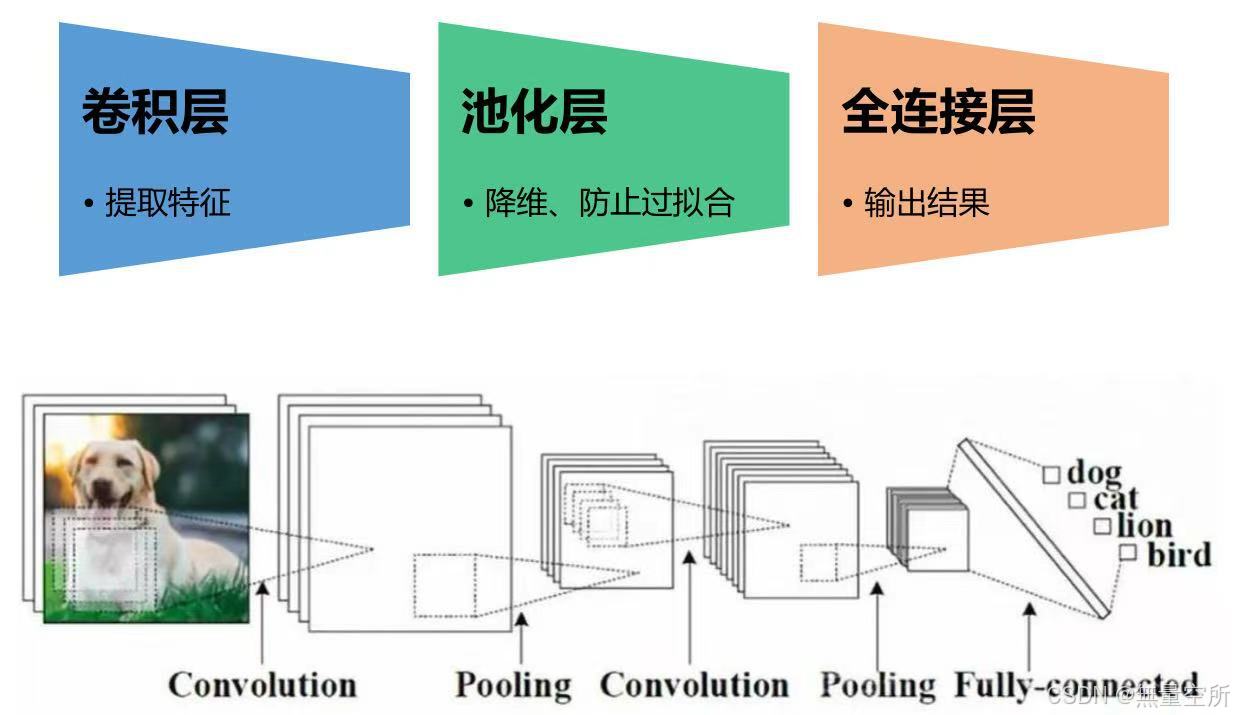
二、网络结构

卷积神经网络在标准的前馈型神经网络的基础上加了一些卷积层和池化层。
典型的卷积神经网络由卷积层、 池化层、 全连接层构成，中间可以有多个卷积层+池化层，最后用全连接层输出结果。

卷积网络层数 = 卷积层数 + 1（全连接层）

2.1 卷积层正向传播过程

2.1.1 卷积

在数字图像处理领域， 卷积是一种常见的运算。 它可以用于图像去噪、 增强、边缘检测等问题， 还可以用于提取图像的特征。

卷积运算用一个称为卷积核（滤波器） 的矩阵从上到下、 从左到右在图像上滑动， 将卷积核矩阵的各个元素与它在图像上覆盖的对应位置的元素相乘， 然后求和， 得到输出值。 

过程如下图所示：

在图像处理中， 卷积核矩阵的数值是根据经验人工设计的， 也可以通过机器学习的手段来自动生成这些卷积核，例如Sobel 算子、 Roberts 算子、 Prewitt 算子等。

卷积神经网络是通过自学习的手段来得到各种有用的卷积核。

经过卷积运算之后图像尺寸变小了， 如果原始图像是 m× n， 卷积核为 s× s，不考虑填充、步幅等，则卷积结果图像的尺寸为：

每个卷积核提取特定特征，图像处理时共享其权重。单卷积层只能处理单一尺度，因此需要多个卷积层来捕捉不同尺度和层次的特征。每个卷积层包含多个卷积核，以提取多样化的特征。

数学公式表示

假设输入图像的子图像在(i , j)位置的像素值为 ， 卷积核矩阵在位置(p , q)的元素值为 。 卷积核作用于图像的某一位置， 得到的输出为：

其中， f 为激活函数， b 为偏置项。 使用激活函数是为了保证非线性。 卷积核参数与偏置项通过学习得到， 与普通神经元类似，卷积核参数即为连接权重， 偏置和普通神经网络的偏置相同， 激活函数也一样。
 

2.1.2 填充（Padding）

当卷积核尺寸大于 1 时， 输出特征图的尺寸会小于输入图片尺寸。 如果经过多次卷积， 输出图片尺寸会不断减小， 边界和角落像素丢失越来越多， 导致模型训练效果不佳。 且当卷积核的高度和宽度不同时， 也可以通过填充(padding)使输入和输出具有相同的宽和高。 填充如下图所示：

2.1.3 步幅（stride）

卷积核每次滑动的大小。上面的例子卷积核每次滑动一个像素点， 步幅为 1。
下图为步幅为 2 的卷积过程：

2.1.4 输出特征图的尺寸计算公式

尺寸 m*m 的特征图，经过 k*k 的卷积层，步幅（stride）=s，填充（padding）=p

输出尺寸：

2.1.5 卷积参数共享

32*32*3的图像，用10个5*5*3的filter来进行卷积操作，一共需要多少个参数

5*5*3*10+10 = 760

最后一个10是偏置项，易忘记 

2.1.6 多层卷积核

前面讲述的是单通道图像卷积， 输入是二维数组。

实际应用时遇到的经常是多通道图像， 如 RGB 彩色图像有3个通道即有3种特征，因此处理时需要有3个卷积核，产生的输出也是多通道的特征图像。

具体做法是用卷积核的各个通道分别对输入图像的各个通道分别对输入图像的各个通道进行卷积， 然后把对应位置处的像素值按照各个通道累加。

由于每一层允许有多个卷积核， 故卷积操作后会输出多张特征图像， 因此， 第  个卷积层每个卷积核的通道数必须与输入特征图像的通道数相同， 即第 层的卷积核通道数等于第 层卷积核的个数。

多通道卷积（1个卷积核）的示意图：

多通道卷积（2个卷积核）的示意图：

2.1.6 感受野

定义：感受野指卷积核在一次卷积操作时对原图像的作用范围， 即神经网络中神经元“看到的” 输入区域， 不同的卷积层有不同的感受野。

网络前面的卷积层感受野小， 用于提取图像细节的信息； 后面的卷积层感受野更大， 用于提取更大范围的、 高层的抽象信息， 这是多层卷积网络的设计初衷。

如下图所示， kernel size 均为 3× 3， 滑动步长均为 1， 绿色标记的是 Layer2 卷积结果每个元素表示的区域， 黄色标记的是 Layer3 表示的区域。

• Layer2 卷积结果每个元素可表示 Layer1 上 3× 3 大小的区域；
• Layer3 卷积结果每个元素表示 Layer2 上 3 × 3 大小的区域， 该区域对应的是 Layer1 上 5× 5 大小的区域。这就对应了前边所说越往后的卷积层感受野越大

3个3*3卷积核感受野 = 1个7*7卷积核感受野，但VGG网络选择3个3*3卷积核

原因：

假设输入大小都是h*w*c，并且都使用c个卷积核(得到c个特征图)，可以来计算-下其各自所需参数:

• 一个7*7卷积核所需参数: Cx(7x7xC)=49 C^2
• 3个3*3卷积核所需参数: 3xCx(3x3xC)= 27 C^2

很明显，堆叠小的卷积核所需的参数更少一些，并且卷积过程越多，特征提取也会越细致，加入的非线性变换也随着增多，还不会增大权重参数个数，这就是VGG网络的基本出发点，用小的卷积核来完成体特征提取操作。

2.2 池化层正向传播过程

通过卷积操作， 完成了对输入图像的降维和特征提取， 但特征图像的维数还是很高。 维数高不仅计算耗时， 而且容易导致过拟合。池化可以完成降维操作，对特征进行精炼操作。

注：维数是描述数据集中的特征数量或空间中独立变量的数量，降维即减少数据的特征数量

池化（Pooling） 操作

进行无重叠的两种 2× 2 池化操作：

平均池化一般在最后一步使用，每一维进行全局平均池化，就可以将一个多维特征图转变成多维向量，用于后续操作 

池化好处

• 降低图像尺寸
• 一定程度的平移、 旋转不变性，因为输出值由图像的一片区域计算得到， 对于小幅度的平移和旋转不敏感。
  如下图所示， 左边是一个标准的 x 图像， 右边是一个被旋转了的 x 图像， 如果我们使用最大池化或均值池化操作， 黄色框里边池化后的值是不变的， 因此， 其对小幅度的旋转是不敏感的。

池化层实现时是在进行卷积操作之后对得到的特征图像进行分块， 图像被划分成不相交的块， 计算这些块内的最大值或平均值， 得到池化后的图像。 均值池化和最大池化都可以完成降维操作， 一般情况下最大池化有更好的效果。

2.2 全连接层正向传播过程

卷积神经网络的全连接层和全连接神经网络相同。

卷积神经网络的正向传播算法与全连接神经网络类似， 只不过输入的是二维或者更高维的图像， 输入数据依次经过每个层， 最后产生输出。 卷积层、 池化层的正向传播计算方法就是前面所说卷积计算和池化操作的过程， 再结合全连接层的正向传播方法， 可以得到整个卷积神经网络的正向传播算法。

三、训练算法

卷积核矩阵为 K：

输入图像为：

卷积之后产生的输出图像是：

对应的误差项为：

3.1 卷积层反向传播算法

rot180 表示矩阵顺时针旋转 180° 的操作。 至此可以根据误差项计算卷积层损失函数对权重和偏置项的偏导数， 并且把误差项通过卷积层传播到了前一层。

3.2 池化层反向传播算法

池化层没有权重和偏置项， 因此， 无需计算本层参数的偏导数以及执行梯度下降更新操作， 所要做的是将误差传播到前一层。

平均池化

将  的每一个元素都扩充为 s× s 个元素

最大池化

对于扩充 s× s 块， 最大值位置处的元素设为 ， 其他位置全部置为 0：

四、残差连接

网络中遇到问题：层数越多，错误率越高

解决方法：引入残差连接，保证至少不比原来差

五、卷积神经网络实现手写数字识别代码

设计一个 3 层的卷积神经网络， 输入图像尺寸为 28× 28；

• 第一个卷积层有 6 个卷积核， 每个卷积核的大小为 5× 5； 第一个池化层采用无重叠的 2× 2最大池化；
• 第二个卷积层有 16 个卷积核， 每个卷积核的大小为 5× 5； 第二个池化层同样采用无重叠的 2× 2 最大池化；
• 最后一层为全连接层， 其神经元个数为16× 5 × 5， 也就是第二个池化层输出的 16 个通道的 5× 5 的图像。
• 卷积层的激活函数使用 ReLU， 输出层的激活函数为 softmax。

4.1 代码分块

1）数据处理

# 定义超参数
num_epochs = 1
batch_size = 64
learning_rate = 0.01

# 加载和预处理数据
train_dataset = MNIST(root='./', train=True, transform=transforms.ToTensor(), download=False)
test_dataset = MNIST(root='./', train=False, transform=transforms.ToTensor(), download=False)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)

2）模型设计

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2)
        self.relu1 = nn.ReLU()
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        self.relu2 = nn.ReLU()
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.fc1 = nn.Linear(in_features=16*5*5, out_features=10)

    def forward(self, x):
        x = self.pool1(self.relu1(self.conv1(x)))
        x = self.pool2(self.relu2(self.conv2(x)))
        x = x.view(-1, 16*5*5)  # Flatten
        x = self.fc1(x)
        return nn.functional.softmax(x, dim=1)

3）训练模型

# 训练模型
def train(model, train_loader, optimizer, criterion, epochs):
    model.train()
    for epoch in range(epochs):
        for i, (images, labels) in enumerate(train_loader):
            optimizer.zero_grad()
            outputs = model.forward(images)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            if i % 100 == 0:
                print(f"Epoch [{epoch + 1}/{epochs}], step {i + 1}/{len(train_loader)}, Loss: {loss.item()}")

# 初始化模型、损失函数和优化器
model = CNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

# 训练模型
train(model, train_loader, optimizer, criterion, epochs=num_epochs)

4）保存模型

# 模型保存
torch.save(model.state_dict(), 'cnn_state_dict.pth')

5）测试模型

# 测试模型
def predict(model, test_loader):
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for images, labels in test_loader:
            outputs = model.forward(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print(f'Accuracy on test set: {100 * correct / total:.2f}%')

# 加载模型
model = CNN()
model.load_state_dict(torch.load('cnn_state_dict.pth'))
predict(model, test_loader)

4.2 完整代码 

# python --version     3.8.10
# PyTorch --version   2.3.1
# torchvision --version 0.18.1
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST


# 定义超参数
num_epochs = 1
batch_size = 64
learning_rate = 0.01


# 加载和预处理数据
train_dataset = MNIST(root='./', train=True, transform=transforms.ToTensor(), download=False)
test_dataset = MNIST(root='./', train=False, transform=transforms.ToTensor(), download=False)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)


# 定义CNN模型
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2)
        self.relu1 = nn.ReLU()
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        self.relu2 = nn.ReLU()
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.fc1 = nn.Linear(in_features=16*5*5, out_features=10)

    def forward(self, x):
        x = self.pool1(self.relu1(self.conv1(x)))
        x = self.pool2(self.relu2(self.conv2(x)))
        x = x.view(-1, 16*5*5)  # Flatten
        x = self.fc1(x)
        return nn.functional.softmax(x, dim=1)


# 训练模型
def train(model, train_loader, optimizer, criterion, epochs):
    model.train()
    for epoch in range(epochs):
        for i, (images, labels) in enumerate(train_loader):
            optimizer.zero_grad()
            outputs = model.forward(images)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            if i % 100 == 0:
                print(f"Epoch [{epoch + 1}/{epochs}], step {i + 1}/{len(train_loader)}, Loss: {loss.item()}")


# 测试模型
def predict(model, test_loader):
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for images, labels in test_loader:
            outputs = model.forward(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print(f'Accuracy on test set: {100 * correct / total:.2f}%')


# 初始化模型、损失函数和优化器
model = CNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

# 训练并测试模型
train(model, train_loader, optimizer, criterion, epochs=num_epochs)

# 模型保存并测试
torch.save(model.state_dict(), 'cnn_state_dict.pth')

# 加载模型
model = CNN()
model.load_state_dict(torch.load('cnn_state_dict.pth'))
predict(model, test_loader)