逻辑回归原理与代码实现

無量空所

已于 2025-03-27 16:22:50 修改

阅读量729

点赞数 21

分类专栏：机器学习文章标签：逻辑回归算法机器学习

于 2025-01-19 15:48:05 首次发布

本文链接：https://blog.youkuaiyun.com/m0_67804957/article/details/145240025

版权

机器学习专栏收录该内容

7 篇文章

订阅专栏

一、逻辑回归 vs 线性回归

比较项	逻辑回归（Logistic Regression）	线性回归（Linear Regression）
目标任务	主要用于分类任务（如二分类、多分类）	主要用于回归任务（预测连续数值）
输出	概率值（通过Sigmoid或Softmax映射到(0,1)范围）	直接输出一个连续值
数学模型	使用Sigmoid函数（或Softmax）将线性组合转换为概率	直接使用线性方程 y=wX+by = wX + b 进行预测
损失函数	交叉熵损失（Cross-Entropy Loss）	均方误差（MSE, Mean Squared Error）
适用场景	是否属于某个类别（如邮件是否垃圾邮件）	预测数值（如房价预测）
结果解释	结果通常通过阈值（如0.5）转换为类别	结果是一个实数

二、sigmoid函数（logistic 函数）

尽管逻辑回归有“回归” 二字，但却是用于分类的模型，它用 sigmoid 函数估计出样本属于正样本的概率。对于一个问题，逻辑回归会拟合一条曲线，如下图所示。

sigmoid 函数可以输出样本 x 是正样本或负样本的概率

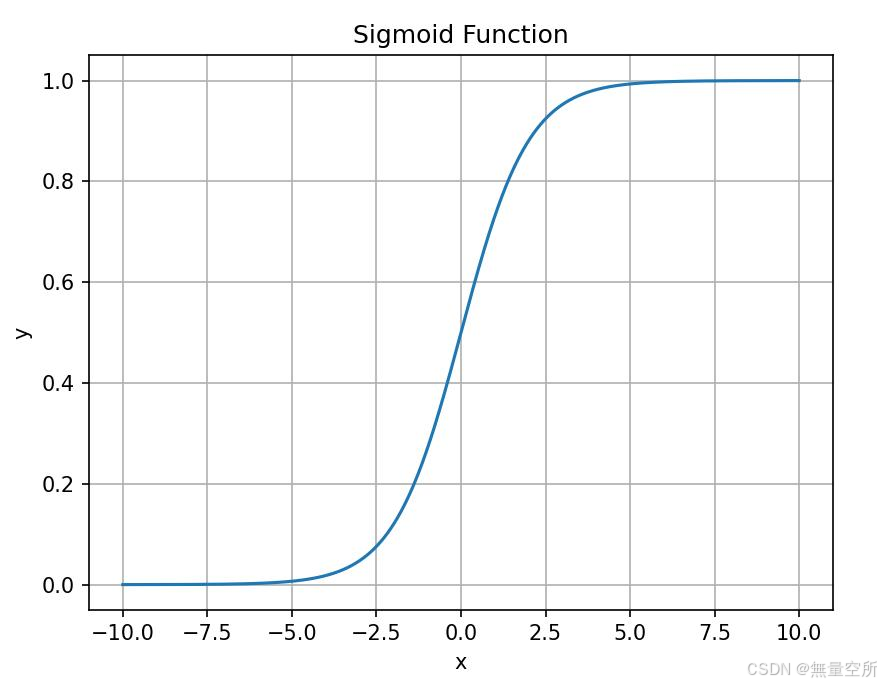
根据函数值很方便地计算出导数值。

通常 sigmoid 函数无法直接用于分类问题，比如肿瘤分类问题的输入特征 x 不可能出现负数，直接使用sigmoid 函数的结果永远是大于等于 0.5 的。下面介绍使用 sigmoid 函数构建逻辑回归模型的步骤：

第一步：用一个线性函数将输入特征向量映射成一个实数 z，表示为 $z = \vec{w} \cdot \vec{x} + b$ 。

第二步：将第一步的 z 作为输入给到 sigmoid 函数，表示为 $g(z) = \frac{1}{1 + e^{-z}}$ 。

把这两步结合就得到了逻辑回归模型： $f_{\vec{w},b}(\vec{x}) = g(\vec{w}\vec{x} + b) = \frac{1}{1 + e^{-(\vec{w}\vec{x} + b)}}$

逻辑回归的输入是一个或一组特征，输出一个 0~1 的实数，可以将这个输出看作是一个概率。即输入特征 x，输出类别为正类的概率。

三、决策边界

逻辑回归模型输出一个概率，那么如何根据这个概率判断其标签是 0 还是1？这里也需要设置一个阈值，通常设置为 0.5，当概率大于 0.5 时，预测标签是1，否则预测标签是 0。

在 sigmoid 函数中，函数值是 0.5的位置对应z=0，所以 $z = \vec{w} \cdot \vec{x} + b =0$ 这条线就是决策边界。

如下图所示的例子，当 $\vec{w} = [1,1],b=-3$ 时，就是我们要找的决策边界。

当参数选择不同时，决策边界也不同，因此，训练逻辑回归模型其本质是要找到合适的决策边界，而 sigmoid 函数是用来确定分类结果的。

四、第一种表述--类别标签为0和1

代价函数用来衡量模型对训练数据集的拟合程度，使模型能够尝试选择更好的参数。均方误差代价函数对于逻辑回归来说并不是一个理想的代价函数，直接使用可能会得到非凸函数，下面介绍另一种代价函数，它可以帮助我们为逻辑回归选择更好的参数。

均方误差代价函数的公式为：

我们可以将其改成写成如下形式：

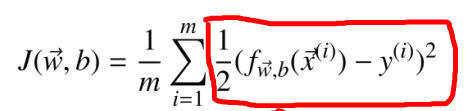
这里给出一个新的术语：损失函数（Loss Function）定义了单个样本预测值与真实值之间的误差。上式中红框部分就是损失函数。损失函数用 $L(f_{\vec{w},b}(\vec{x}), y)$ 表示，它是模型预测值和数据真实值的函数。

下面不再用平方误差作为损失函数，而是换一种方法使代价函数成为一个凸函数。

简化为：

逻辑回归模型的代价函数可以写成：

这个损失函数是通过概率论中的最大似然估计推理出来的， 这样得到的代价函数是一个凸函数，便于使用梯度下降法进行求解。

4.1 逻辑回归中的梯度下降法

计算过程中最重要的部分依然是梯度的计算，在逻辑回归中梯度的计算结果如下：

梯度的计算结果看起来与线性回归中梯度的计算结果是相同的，但实际上模型的定义是不同的。这里 $f_{\vec{w},b}(\vec{x})$ 梯度的计算结果并不是直接沿用线性回归中的结果，而是经过推导之后刚好得到了相同的表示形式。

五、第二种表述--类别标签为+1和-1

一个样本为每一类的概率可以统一写为：

logistic 回归的对数似然函数为

求该函数的极大值等价于求其负函数的极小值，由此得到目标函数为：

牛顿法求解w

思想

多元函数 f(x)在点 x*处取得极值的必要条件是梯度为 0，即 $\nabla f(x^*) = 0$

完整流程

给定初始值 $x_0$ 和精度阈值 $\varepsilon$ ，设置 k=0；
计算梯度和 Hessian 矩阵；
如果 $|| g_k || < \varepsilon$ ，则停止迭代；
计算 $d_k= -H_k^{-1}g_k$
计算新的迭代点 $x_{k+1} = x_k + d_k$ ;
令 $k = k+ 1$ ，返回步骤2

推导步骤

利用迭代法进行计算，避免直接计算函数梯度

多元函数在 $x_0$ 处的二阶泰勒展开为：

忽略二次以上的项，得到函数：

对上式两边同时对 x 求梯度：：

令函数的梯度为 0：

得到

令 $g = \nabla f(x_0)$ ，得到

由于在该过程中省略了高阶项，故这个解并不一定是函数的驻点，需要反复用此公式进行迭代。从初始点 $x_0$ 处开始迭代，计算函数在 $x_k$ 处的 Hessian矩阵 $H_k$ 和梯度向量，然后用下面的公式进行迭代：

直至到达函数的驻点处。其中 $-H_k^{-1}g_k$ ，称为牛顿方向。迭代终止的条件是梯度的模接近于 0，或者函数值下降小于指定阈值。

其中Hessian矩阵为：

与梯度下降法对比

牛顿法有更快的收敛速度，但每一步迭代的成本也更高，在每次迭代时，除了要计算梯度向量之外还要计算 Hessian 矩阵以及 Hessian 矩阵的逆矩阵，所以当参数量很大的时候不适合使用牛顿法进行求解。

六、代码实现

使用威斯康星州乳腺癌数据集实现分类问题，该数据集是scikit-learn（sklearn）库中一个常用的内置数据集，用于分类任务。该数据集包含了从乳腺癌患者收集的肿瘤特征的测量值，以及相应的良性（benign）或恶性（malignant）标签。数据集包含 30 个数值型特征，这些特征描述了乳腺肿瘤的不同测量值，如肿瘤的半径、纹理、对称性等。数据集的目标变量是二分类的，代表肿瘤的良性（benign）或恶性（malignant）状态。数据集包含 569 个样本，其中良性样本 357 个，恶性样本 212 个。

1、手动梯度下降法实现

import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 加载数据集
data = load_breast_cancer()
X = data.data
y = data.target

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)


# sigmoid函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))


# 损失函数
def loss_function(X, y, theta):
    m = len(y)
    h = sigmoid(np.dot(X, theta))
    loss = (-1/m) * np.sum(y * np.log(h) + (1 - y) * np.log(1 - h))
    return loss


# 梯度下降法优化
def gradient_descent(X, y, theta, learning_rate=0.01, max_iters=0, tol=1e-6):
    m = len(y)
    iters = 0
    while iters < max_iters:
        grad = (1/m) * np.dot(X.T, (sigmoid(np.dot(X, theta)) - y))
        theta -= learning_rate * grad
        # 计算损失值
        loss = loss_function(X, y, theta)
        # 判断是否收敛
        if np.linalg.norm(grad) < tol:
            break
        iters += 1
    return theta


# 添加一列常数项1到特征矩阵中
X_train = np.hstack((np.ones((X_train.shape[0], 1)), X_train))
X_test = np.hstack((np.ones((X_test.shape[0], 1)), X_test))

# 初始化参数向量theta
theta = np.zeros(X_train.shape[1])

# 使用梯度下降法优化参数
theta = gradient_descent(X_train, y_train, theta, max_iters=1000)

# 计算训练集的准确率
predictions_train = sigmoid(np.dot(X_train, theta)) >= 0.5
accuracy_train = np.mean(predictions_train == y_train)
print("训练集准确率:", accuracy_train)

# 计算测试集的准确率
predictions_test = sigmoid(np.dot(X_test, theta)) >= 0.5
accuracy_test = np.mean(predictions_test == y_test)
print("测试集准确率:", accuracy_test)

2、手动牛顿法实现

import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 加载数据集
data = load_breast_cancer()
X = data.data
y = data.target

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)


def sigmoid(x):
    # 使用clip将输入限制在一个合理的范围内
    return 1 / (1 + np.exp(-np.clip(x, -500, 500)))


# 修改后的损失函数
def loss_function(X, y, theta):
    m = len(y)
    h = sigmoid(np.dot(X, theta))
    # 添加一个很小的数epsilon，防止log函数中出现0
    epsilon = 1e-5
    loss = (-1/m) * np.sum(y * np.log(h + epsilon) + (1 - y) * np.log(1 - h + epsilon))
    return loss


# 损失函数的导数
def gradient(X, y, theta):
    m = len(y)
    h = sigmoid(np.dot(X, theta))
    grad = (1/m) * np.dot(X.T, (h - y))
    return grad


# 损失函数的Hessian矩阵（二阶导数）
def hessian(X, theta):
    m = X.shape[0]
    h = sigmoid(np.dot(X, theta))
    H = (1/m) * X.T @ np.diag(h) @ np.diag(1 - h) @ X #@表示矩阵乘法
    return H


# 牛顿法优化
def newton_method(X, y, theta, max_iters=0, tol=1e-6, alpha=0.1):

    iters = 0
    while iters < max_iters:
        grad = gradient(X, y, theta)
        H = hessian(X, theta)
        try:
            # 使用np.linalg.pinv计算海森矩阵的逆矩阵
            delta = np.linalg.solve(H, grad)
        except np.linalg.LinAlgError:
            # 如果计算失败，添加正则化项alpha*I到海森矩阵
            delta = np.linalg.solve(H + alpha * np.eye(H.shape[0]), grad)
        theta -= delta
        # 计算损失值
        loss = loss_function(X, y, theta)
        # 判断是否收敛
        if np.linalg.norm(delta) < tol:
            break
        iters += 1
    return theta


# 添加一列常数项1到特征矩阵中
X_train = np.hstack((np.ones((X_train.shape[0], 1)), X_train))
X_test = np.hstack((np.ones((X_test.shape[0], 1)), X_test))

# 初始化参数向量theta
theta = np.zeros(X_train.shape[1])

# 使用牛顿法优化参数
theta = newton_method(X_train, y_train, theta, max_iters=1000)

# 计算训练集的准确率
# predictions_train = logistic(np.dot(y_train, np.dot(X_train, theta))) >= 0.5
predictions_train = sigmoid(np.dot(X_train, theta)) >= 0.5
accuracy_train = np.mean(predictions_train == y_train)
print("训练集准确率:", accuracy_train)

# 计算测试集的准确率
# predictions_test = logistic(np.dot(y_test, np.dot(X_test, theta))) >= 0.5
predictions_test = sigmoid(np.dot(X_test, theta)) >= 0.5
accuracy_test = np.mean(predictions_test == y_test)
print("测试集准确率:", accuracy_test)

3、sklearn实现

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler

# 1. 加载数据集
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
# 数据归一化处理
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 2. 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. 实例化逻辑回归模型
logreg = LogisticRegression(max_iter=1000)  # 设置最大迭代次数，因为逻辑回归需要多次迭代来收敛

# 4. 使用训练数据拟合模型
logreg.fit(X_train, y_train)

# 5. 使用测试数据评估模型性能
y_pred = logreg.predict(X_test)

accuracy = accuracy_score(y_test, y_pred)
print("Accuracy: {}".format(accuracy))