机器学习——主成分分析（PCA）

最新推荐文章于 2025-02-19 23:57:58 发布

原创最新推荐文章于 2025-02-19 23:57:58 发布 · 1.7k 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能

本文介绍了PCA（主成分分析）的基本原理、步骤，以及如何在机器学习和人脸识别中应用，特别是用于降维和图像处理。PCA通过找到数据方差最大的方向进行数据压缩，降低计算成本，但在处理非线性数据时效果不佳。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一：概述

1.1原理与核心思想

PCA是Principal Component Analysis的缩写，主成分分析的目的是通过线性变换将原始数据变换为一组各维度线性无关的表示，这些表示被称为主成分。主成分分析的原理是通过找到数据中方差最大的方向，将数据投影到这个方向上，从而实现数据的降维。PCA的核心思想是通过特征值分解或奇异值分解来找到数据的主成分，从而实现数据的降维和去相关。

1.2应用场景

在机器学习中，当升维升到一定程度之后，机器学习也会很难处理，会造成维数灾难，因此需要找到一个方法，来对其进行合理的降维。主成分分析与因子分析就属于这类降维的方法。

在数学建模中，PCA可以应用于多个领域，例如金融、医学、自然语言处理等。

在图像处理中，如果要识别人脸，需要将每张图像表示为一个向量，每个元素代表图像中某个像素点的灰度值。由于每张图像的像素数量很大，可能成百上千万甚至更多，这就是导致会导致计算和存储成本非常高。这时候就可以使用PCA对这些向量进行降维，将每张图像表示为一个包含较少元素的向量，并且，PCA还能够从这些低维向量中提取出最具代表性的信息，以便于后续人脸识别。

如图所示：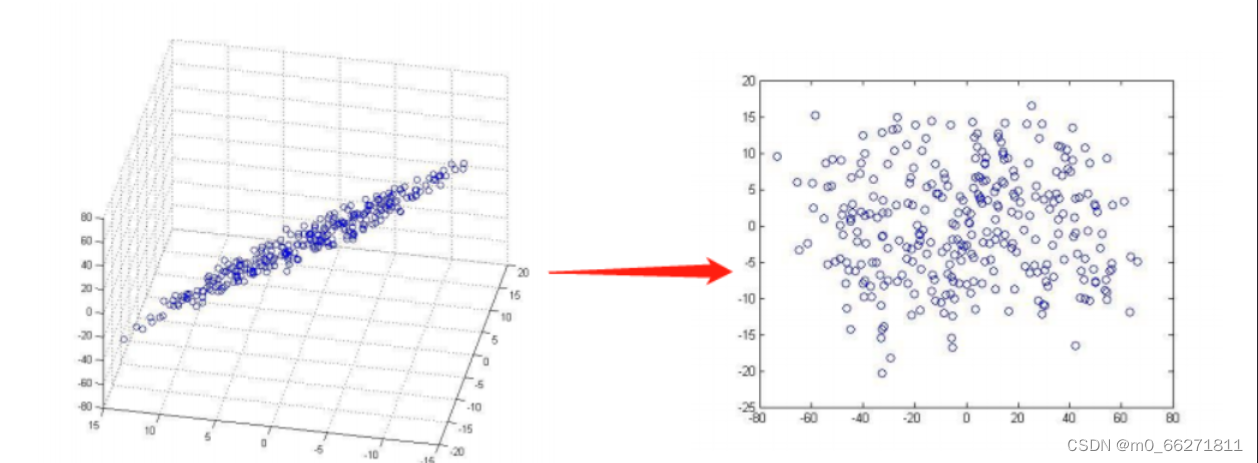

二：PCA基本步骤

假设有n各个样本，p个指标，则会构成大小为n*p的样本矩阵

1.数据预处理

2.计算协方差矩阵

3.对协方差矩阵做特征值分解并计算出特征向量

4.计算并写出主成分

一般取累计贡献超过80%的特征值所对应的第一，第二，..第m个主成分

5.依据所求的主成分进行后续结果计算分析

三：利用PCA进行人脸识别

1.数据准备

本次实验的数据集ORL-Faces包含40个人，每人拥有10张正脸照片，取每个人的7张照片，作为训练数据。那么每个人剩下的3张照片，计算机还没有看过，就可以在计算机认识了每一个人之后用来考验计算机是否真的能够正确识别图像中的人是谁。

2.创建每个训练样本组成的M*N矩阵


bigList = []
# 导入人脸模型库
faceCascade = cv2.CascadeClassifier(r'C:\Python\haarshare\haarcascade_frontalface_alt.xml')
# 遍历30个人
for i in range(1, 31):
    # 遍历每个人的7张照片
	for j in range(1, 8):
		list = []
        # 直接读入灰度照片
		image = cv2.imread("C:\\Users\\tangyitao\\Pictures\\Saved Pictures\\trainFace\\train"
								+ str(i) + "\\train" + str(i) + "" + str(j) + ".jpg", 0)
		faces = faceCascade.detectMultiScale(image, 1.3, 5)
		for (x, y, w, h) in faces:
            # 裁剪人脸区域为 128 * 128 大小
			cutResize = cv2.resize(image[y:y + h, x:x + w], (128, 128),
										interpolation=cv2.INTER_CUBIC)  
        # 遍历图片行数
		for x in range(cutResize.shape[0]):
            # 遍历图片每一行的每一列
			for y in range(cutResize.shape[1]):
                # 将每一处的灰度值添加至列表
				list.append(cutResize[x, y]) 
		bigList.append(list)
print("\n\ntrainFaceMat ")
trainFaceMat = numpy.mat(bigList)  # 得到训练样本矩阵
print("trainFaceMat.shape[0] ",trainFaceMat.shape[0])
print("trainFaceMat.shape[1]",trainFaceMat.shape[1])
print(trainFaceMat)

这里我们把每个训练样本的照片都处理成了128*128

3.得到规格化的训练样本数据


 
meanFaceMat = numpy.mean(trainFaceMat, axis=0)  # 每一列的和除行数，得到平均值
print("meanFaceMat \n\n")
print("meanFaceMat.shape[0] ",meanFaceMat.shape[0])
print("meanFaceMat.shape[1] ",meanFaceMat.shape[1])
print(meanFaceMat)
normTrainFaceMat = trainFaceMat - meanFaceMat
print("\n\n normTrainFaceMat")
print("normTrainFaceMat.shape[0]  ",normTrainFaceMat.shape[0])
print("normTrainFaceMat.shape[1]  ",normTrainFaceMat.shape[1])
print(normTrainFaceMat)

4.计算协方差矩阵并求的特征值和特征向量

covariance = numpy.cov(normTrainFaceMat)
# 求得协方差矩阵的特征值和特征向量
eigenvalue, featurevector = numpy.linalg.eig(covariance)

5.对特征值进行排序并保留k个最大特征值的特征向量

sorted_Index = numpy.argsort(eigenvalue)
topk_evecs = featurevector[:,sorted_Index[:-140-1:-1]]

6.计算投影

7.创建测试样本矩阵

# 主要思想和第一步计算trainFaceMat差不多,这里只需要添加一张照片的数据
list = []
faceCascade = cv2.CascadeClassifier(r'C:\Python\haarshare\haarcascade_frontalface_alt.xml')
# fileName 为待识别图片的文件名,读入灰度人脸
image = cv2.imread(fileName, 0)
faces = self.faceCascade.detectMultiScale(self.image, 1.3, 5)
for (x, y, w, h) in self.faces:
	cut = image[y:y + h, x:x + w]
	# 处理成 128 * 128大小的人脸
	cutResize = cv2.resize(cut, (128, 128), interpolation=cv2.INTER_CUBIC)
for x in range(cutResize.shape[0]):
	for y in range(cutResize.shape[1]):
		list.append(cutResize[x, y])
testFaceMat = numpy.mat(list)

8.进行规格化

normTestFaceMat = testFaceMat - meanFaceMat

9.计算欧式距离找到匹配人脸


eigen_test_sample = numpy.dot(normTestFaceMat, eigenface)
# 以 eigen_train_sample[0]与eigen_test_sample的欧式距离赋值 minDistance
minDistance = numpy.linalg.norm(eigen_train_sample[0] - eigen_test_sample)
# num 记录训练集中第几个人与待识别人为同一人
num = 1
# 遍历 eigen_train_sample 的每一行，在此处，eigen_train_sample.shape[0] = 210。
for i in range(1, eigen_train_sample.shape[0]):
    distance = numpy.linalg.norm(eigen_train_sample[i] - eigen_test_sample)
	if minDistance > distance:
		minDistance = distance
        # 30个人中，每个人有7张照片，i是记录的第几张照片
        # 因此记录第几个人的num为 i // 7 + 1。
		num = i // 7 + 1

10.得到最终结果

四：总结

PCA作为机器学习中经典的线性降维算法，通过”最小重构误差“为目标导向对数据进行投影实现降维，如今仍然在机器学习许多领域（语言图像处理、数据可视化）有优异表现。它在降低数据复杂性，降低运算量上有显著优势。但作为一种无监督学习方法（对训练样本没有做标注），在对数据完全无知的情况下，PCA并不能得到较好的保留数据信息并且有可能损失重要信息，且PCA对于主成分的分析判断是影响实验结果的重要因素，另外，PCA对于非线性的数据降维效果较差，我们在进行非线性数据降维时最好采用其它方法。