简单几步教你搞定LIS，LCS，LICS问题

LIS，LCS，LICS都是dp中的基础模型，

今天在复习最长公共上升子序列问题时将这三类问题简单总结了一下

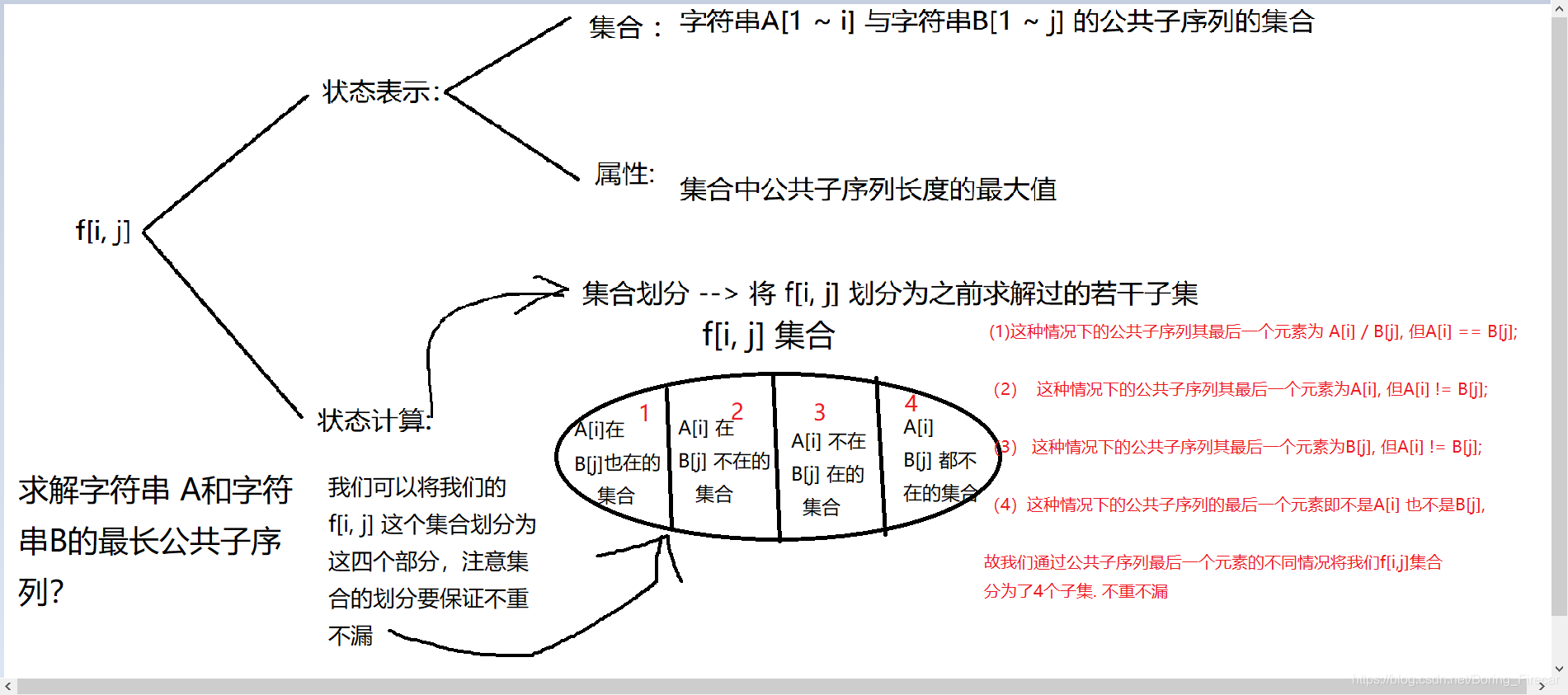
LCS（最长公共子序列）

描述的是给定两个数列，求两数列中的最长公共子序列长度。

状态定义：

f (i, j) 为以数列a的前i个数以及数列b的前j个数组成的最长公共子序列长度

转移方程:

f(i, j) = f(i - 1,j - 1) + 1 (i, j > 0,a[i] == b[j])

f(i, j) = max(f (i - 1, j),f(i, j - 1) ) (i, j > 0, a[i] != b[j] );

LIS（最长上升子序列）

描述的是给定一个数列，求此数列中的最长上升子序列长度

状态定义：

f(j) 为以给定数列a[j]为结尾的最长上升子序列长度

转移方程：

f[j] = max f[j] + 1;(j < i,a[j] < a[i] )

LICS (最长公共上升子序列）

描述的是给定两个数列，求两数列中最长公共上升子序列的长度

状态定义：

f(i, j) 为 数列a的前i个元素 以及 数列 b 的 前j个元素 且以b[j]为结尾的LICS长度

t 为最长LICS的结尾元素位置

转移方程：

f[i][j] = f[i - 1][j] (a[i] != b[j])

f[i][j] = max(f[i - 1][j],f[i - 1][t] + 1) (a[i] == b[j])