数据结构，树，基础-优快云博客

孩子表示法
#define MAX_TREE_SIZE 100
/*孩子结点*/
typedef struct CTNode{
	int child;
	struct CTNode *next;
}*ChildPtr;
/*表头结点*/
typedef struct{
	TElemType data;
	ChildPtr firstchild;
}CTBox;
/*树结构*/
typedef struct{
	CTBox nodes[MAX_TREE_SIZE];	//结点数组
	int r, n;	//根的位置和结点数
}

双亲表示法：

typedef struct BTNode
{
	int data;
	struct BTNode* lChild;
	struct BTNode* rChild;
}BTNode;
//添加节点 
a1->lChild=a2;
a1->rChild=a3;

a2->lChild=NULL;
a2->rChild=NULL;

孩子兄弟表示法：

操作：树的左指针指向自己的第一个孩子，右指针指向与自己相邻的兄弟。

通过孩子兄弟表示法，任意一棵普通树都可以相应转化为一棵二叉树


typedef struct CSNode{
	TElemtype data;
	struct CSNode *firstchild, *rightsib;
} CSNode, *CSTree;

树与二叉树的相互转换：

如图，把黄色线连接，红色叉的线去掉，其实就是使用孩子兄弟表示法

变形后得到下列树

树的遍历：

层序遍历：（运用队列）

从根节点开始，一层一层，从上到下，每层从左到右，依次打印

void level (BTNode *bt)
if (bt != NULL)
{
	int front, rear;
    BTNode *que [maxSize];
	front =rear = 0;
    BTNode *p;
    rear =(rear +1)% maxSize;
	que [rear] = bt;
    while (front !=rear){
    	front =(front + 1)% maxSize;
		p=que[front];
        visit(p);
        if(p->lChild != NULL){
        	rear = (rear + 1)% maxSize;
			que [rear] =p->lChild;
        }
        if(p->rChild != NULL){
        	 rear =(rear + 1)% maxsize;
			 que [rear] =p->rChild;
        }
    }
}

深度优先遍历递归算法：

1.先序遍历

void ShowXianXu(BitTree T)			
{
	if(T==NULL)						
	{
		return;
	}
	printf("%d ",T->data);
	ShowXianXu(T->lchild);			
	ShowXianXu(T->rchild);			
}

2.中序遍历

void ShowZhongXu(BitTree T)			//		先序遍历二叉树
{
	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{
		return;
	}
	
	ShowZhongXu(T->lchild);			//	递归遍历左子树
	printf("%d ",T->data);
	ShowZhongXu(T->rchild);			//	递归遍历右子树
	
}

3.后序遍历

void ShowHouXu(BitTree T)			//		后序遍历二叉树
{
	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{
		return;
	}
	
	ShowHouXu(T->lchild);			//	递归遍历左子树
	ShowHouXu(T->rchild);			//	递归遍历右子树
	printf("%d ",T->data);
}

深度优先遍历非递归算法：运用栈

1.先序遍历：

注意，栈先进后出，下面先右孩子，再左孩子

void preorderNonrecursion (BTNode *bt)
if(bt !=NULL)
{
	BTNode *Stack [maxSize];
	int top = -l;
    BTNode *p =NULL;Stack[++top]= bt;
	while(top!=-1){
		p= Stack[top--];
		Visit(p);
        if(p->rChild! =NULL)
            Stack[++top] =p->rChild;
		if(p->lChild! =NULL)
		   Stack [++top] = p->lChild;
	}
}

2.中序遍历

void postorderNonrecursion(BTNode *bt)
if(bt!=NULL)
{
	BTNode *Stackl [maxsize];
	int topl=-l;BTNode *Stack2[maxSize];
	int top2=-1;BTNode *p =NULL;
    Stack1 [ ++top1] = bt;
	while (top1 != -1){
		p=Stack1 [top1--];
		Stack2[++top2]=p;
		if (p->lChild !=NULL)
           Stack1[++top1] -p->lChild;
		if (p->rChild != NULL)
           Stack1[++top1] =p->rChild;
        while (top2 != -1){
        	p= Stack2[top2--]
			visit(p);
        }
    }
}

3.后序遍历

后序遍历与先序遍历的联系：

先序：根左右

逆后序：根右左

故我们多设置一个栈，用来存放逆后序序列，然后转换成后序序列即可

void inorderNonrecursion (BTNode *bt)
if(bt !=NULL)
   BTNode *Stack[maxSize];
   int top = -l;
   BTNode *p =NULL;
   p= bt;
while(top != -1 || p != NULL){
	while(p != NULL){
		stack[++top]=p;
		p = p->1Child;
	}
    if(top != -1){
    	p= stack[top--];
		visit(p);
        p= p->rChild;
    }
}

线索二叉树：

二叉树的线索化是将二叉链表中的空指针改为指向前驱或后继的线索。而前驱或后继的信息只有在遍历时才能得到，因此线索化的实质就是遍历一次二叉树，线索化的过程就是在遍历的过程中修改空指针的过程。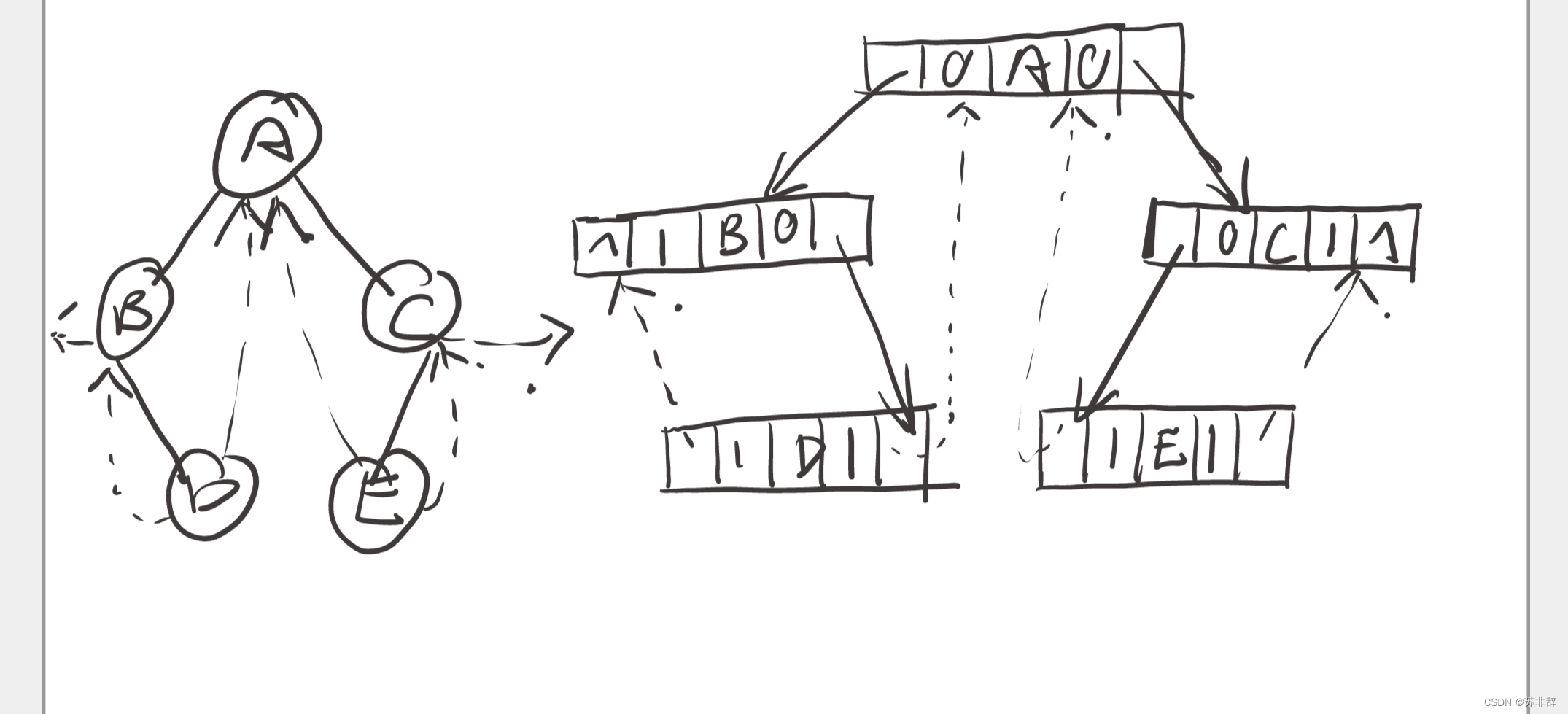

先序线索化

void preThread (TBTNode *p, TBTNode * &pre)
{
	if(p != NULL){
		if(p->lChild == NULL)
		  {
		  	p->lchild =pre;
			p->lTag = l;
		  }
        if(pre !=NULL && pre->rChild == NULL)
		  {
		  	pre->rChild =p;
			  pre->rTag = 1;
          }
        pre = p;
        preThread(p->lchild, pre);
        preThread(p->rChild, pre);
    }
}

中序线索化

void InThread(ThreadTree p, ThreadTree pre){
	if(p != NULL){
		InThread(p->lchild, pre);	//递归，线索化左子树
		if(p->lchild == NULL){	//左子树为空，建立前驱线索
			p->lchild = pre;
			p->ltag = 1;
		}
		if(pre != NULL && pre->rchild == NULL){
			pre->rchild = p;	//建立前驱结点的后继线索
			pre->rtag = 1;
		}
		pre = p;	//标记当前结点成为刚刚访问过的结点
		InThread(p->rchild, pre);	//递归，线索化右子树
	}
}

后序线索化：

void postThread (TBTNode *p, TBTNode * &pre)
{
	if(p != NULL){
		postThread(p->lchild, pre);
        postThread(p->rChild, pre);
		if(p->lChild == NULL)
		  {
		  	p->lchild =pre;
			p->lTag = l;
		  }
        if(pre !=NULL && pre->rChild == NULL)
		  {
		  	pre->rChild =p;
			  pre->rTag = 1;
          }
        pre = p;
    }
}

哈夫曼树：

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，则称该二叉树为哈夫曼树，也被称为最优二叉树。

哈夫曼树的构建
构建思路
下面给出一个非常简洁易操作的算法，来构造一棵哈夫曼树：
1、初始状态下共有n个结点，结点的权值分别是给定的n个数，将他们视作n棵只有根结点的树。
2、合并其中根结点权值最小的两棵树，生成这两棵树的父结点，权值为这两个根结点的权值之和，这样树的数量就减少了一个。
3、重复操作2，直到只剩下一棵树为止，这棵树就是哈夫曼树。