图
1.1 图的基本概念
1.1.1 图的定义
图由顶点集V(G)和边集E(G)组成,记为G=(V,E)。 其中E(G)是边的有限集合,边是顶点的无序对(无向图)或有序对(有向图)。
对有向图来说,E(G)是有向边(也称弧(Arc))的有限集合,弧是顶点的有序对,记为<v,w>,v、w是顶点,v为弧尾(箭头根部),w为弧头(箭头处)。
对无向图来说,E(G)是边的有限集合,边是顶点的无序对,记为(v, w)或者(w, v),并且(v, w)=(w,v)。
示例:
G=(V,E)
V={1,2,3,4,5,6}
E={(1,2),(2,3),(3,4),(4,5),(1,5),(5,6),(2,6),(3,6)}
注意:
• 线性表有空表,树有空树,但图没有空图
• 图的顶点集V一定非空,但边集E可以为空
• |V|表图G中顶点的个数,也称图G的阶
• |E|表图G中边的个数
1.1.2 图的基本术语
1.1.2.1 无向图
全部由无向边构成的图

1.1.2.2 有向图
全部由有向边构成的图

1.1.2.3 简单图、多重图
简单图:不存在重复边,不存在顶点到自身的边
多重图:两个顶点之间的边数大于1
1.1.2.4 完全图(简单完全图)
任意两个结点都有直接路径
完全无向图:边数为
n
(
n
−
1
)
2
\frac{n(n−1)}{2}
2n(n−1)
完全有向图:边数为
n
(
n
−
1
)
{n}{(n−1)}
n(n−1)


1.1.2.5 子图、生成子图
G的子图:所有的顶点和边都属于图G的图
G的生成子图:含有G的所有顶点的子图

1.1.2.6 无向图的连通、连通图、连通分量
v和w连通:无向图中,v到w的路径存在
连通图:图中任意两个顶点都是连通的
连通分量:无向图中的极大连通子图
1.1.2.7 有向图的强连通图、强连通分量
v和w强连通:有向图中,从v到w和从w到v都有路径
强连通图:图中任何一对顶点都是强联通的
强连通分量:有向图中的极大连通子图
1.1.2.8 生成树,生成森林
生成树:包含图中全部顶点的一个极小连通图
生成森林:非连通图中,连通分量的生成树构成了非连通图的生成森林
1.1.2.9 顶点的度、入度、出度
顶点的度Degree:图中与该顶点相关联边的数目
入度:指向该顶点的边的数目
出度:从该顶点出去的边的数目
顶点的度 = 出度 + 入度
对于具有n个顶点, e条边的有向图, 出度和=入度和=e
对于具有n个顶点, e条边的无向图, 度和=2e

1.1.2.10 边的权和网
权Weight:边上的数值
网Network:边上标识权的图

1.1.2.11 稠密图、稀疏图
稠密图:边多
稀疏图:边少

1.1.2.12 路径、路径长度、回路
路径Path:在一个图中,路径是从顶点u到顶点v所经过的顶点序列
路径长度:该路径上边的数目
回路:第一个顶点和最后一个顶点相同的路径
1.1.2.13 简单路径、简单回路
简单路径:顶点不重复出现的路径(ABCDE无重复)
简单回路:除第一个和最后一个顶点,其余顶点不重复出现的回路(ABCDEA无重复)
1.1.2.14 距离
从u到v的距离:从u到v的最短路径长度
1.1.2.15 有向树
有向树:一个顶点的入度为0,其余顶点的入度均为1的有向图
1.1.3 图的结论
1.1.3.1 边数和度数的关系
无向图边数*2 = 各顶点度数之和
有向图边数 = 各顶点的入度之和 = 各顶点的出度之和
1.1.3.2 完全图的边数
完全无向图:边数为
n
(
n
−
1
)
2
\frac{n(n−1)}{2}
2n(n−1)
完全有向图:边数为 n(n−1)
1.1.3.3 连通图生成树
一个连通图的生成树是一个极小连通子图,是无环的
1.1.3.4 连通图的边数
对于一个有n个顶点的图
若是连通无向图,其边的个数至少为n-1(边最少即构成一棵树的情形)
若是强连通有向图,其边的个数至少是n(边最少即构成一个有向环的情形
1.1.3.5 图的存储问题
- 求有向图节点的入度,必须遍历整个邻接表
- 有向图邻接表中,删除某个顶点的所有边的时间复杂度 = O(n+e)
- 一个图的领接矩阵表示唯一, 邻接表表示不唯一
1.1.3.6 图的应用问题
- 最短路径一定是简单路径
- 求最短路径是允许图有环的
- 一个有向图的定点不能排成一个拓扑序列,表明其中存在一个顶点数目大于1的回路,该回路构成一个强连通分量
- 若有向无环图的拓扑序列唯一,不能唯一确定该图
1.1.4 图的操作
| 函数 | 作用 |
|---|---|
| Adjacent(G,x,y) | 判断是否存在边 |
| Neighbors(G,x) | 列出图中与结点x邻接的边 |
| InsertVertex(G,x) | 在图中插入顶点x |
| DeleteVertex(G,x) | 在图中删除顶点x |
| AddEdge(G,x,y) | 若无向边或有向边不存在,则向图中添加该边 |
| RemoveEdge(G,x,y) | 若无向边或有向边存在,则向图中删除该边 |
| NextNeighbor(G,x,y) | 假设图中顶点y是顶点x的一个邻接点 返回除y外的顶点x的下一个邻接点的顶点号 若y是x的最后一个邻接点,则返回1 |
| Get_Edge_Value(G,x,y) | 获取图中边对应的权值 |
| Set_Edge_Value(G,x,y,v) | 设置图中边对应的权值 |
1.2 图的存储方式
1.2.1 邻接矩阵
- 用两个数组来表示图
- 一个一位数组存储图中顶点信息
- 一个二维数组存储图中的边或弧的信息

1.2.2 邻接表
- 领接表是由两部分组成
- 顶点用一个一维数组存储
- 每个顶点的所有领接点构成一个线性表
- 由于领接点的个数不定,所以用单链表存储
- 无向图称为顶点vi的边表
- 有向图则称为顶点vi作为弧尾的出边表

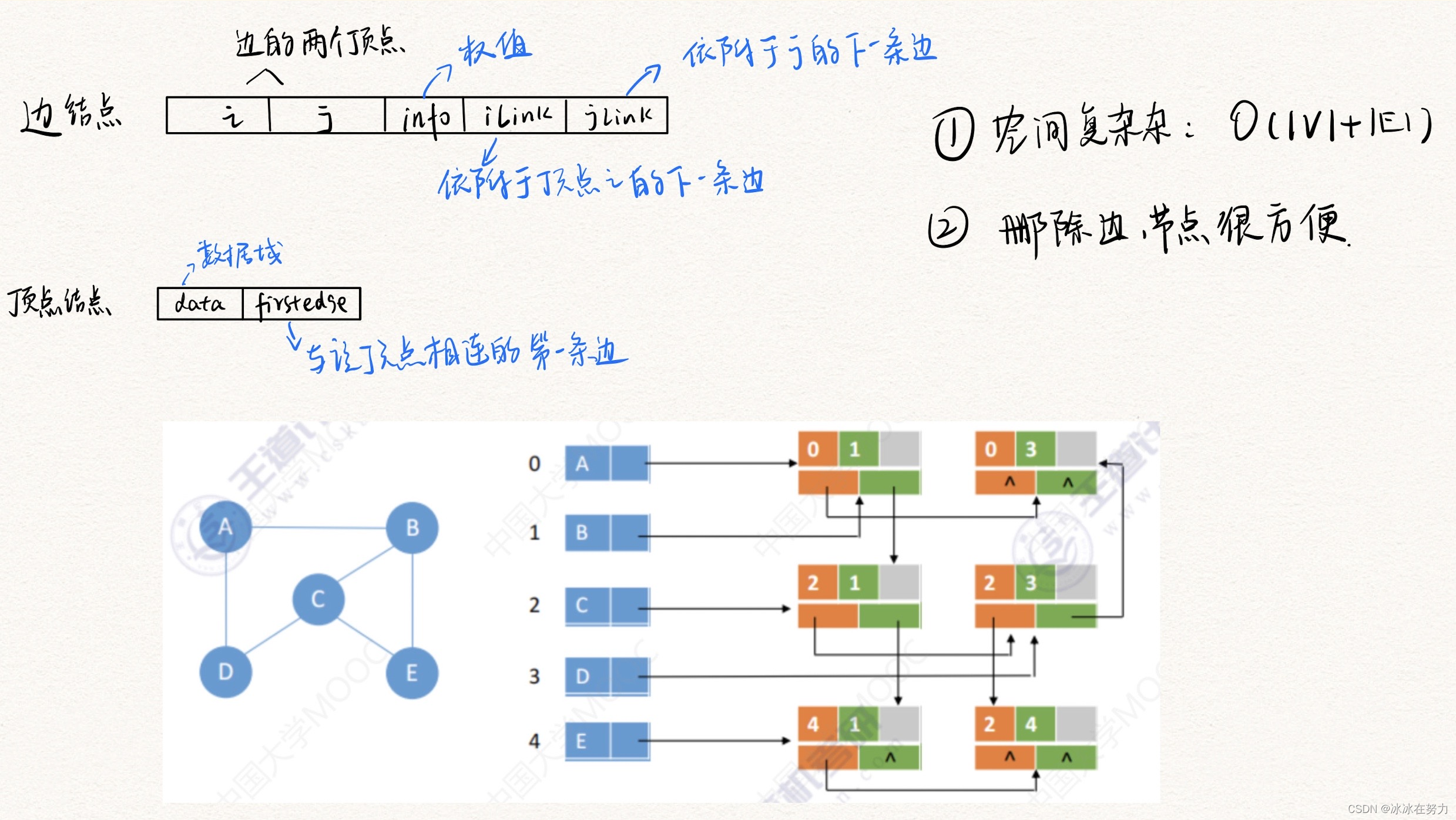
1.2.3 十字链表
- 把邻接表和逆邻接表整合在了一起
- 既容易找到以vi为尾的弧,也容易找到以vi为头的弧
- 容易求得顶点的出度和入度
- 创建图算法的时间复杂度和邻接表相同

1.2.4 领接多重表
- 仿照十字链表的方式,对边表结点的结构进行一些改造
- 同一条边在邻接表中用两个结点表示,而在邻接多重表中只有一个结点
1.3 图的遍历
1.3.1 深度优先搜索DFS
1.3.1.1 定义和复杂度
- 相当于树的先序遍历
- 根节点就是任意出发的节点
- 子节点就是所有邻近的未访问过的节点
| 存储方式 | 时间复杂度 |
|---|---|
| 邻接表存储 | O ( N + E ) O(N+E) O(N+E) |
| 邻接矩阵存储 | O ( N 2 ) O(N^2) O(N2) |
1.3.1.2 遍历过程
不撞南墙不回头,撞墙就回头,按照visited表从小到大走

1.3.1.3 生成树

1.3.1.4 生成森林

1.3.2 广度优先搜索BFS
1.3.2.1 定义和复杂度
相当于树的层序遍历
| 存储方式 | 时间复杂度 |
|---|---|
| 邻接表存储 | O ( N + E ) O(N+E) O(N+E) |
| 邻接矩阵存储 | O ( N 2 ) O(N^2) O(N2) |
1.3.2.2 遍历过程

1.3.2.3 生成树

1.3.2.4 生成森林

1.4 图的应用
1.4.1 最小生成树
1.4.1.1 定义
图G的所有生成树中边的权值之和最小的树
1.4.1.2 性质
- 最小生成树并不是唯一的
- 当图G中的各边权值不相等时,最小生成树是唯一的
- 当G本身就是一棵树时,其最小生成树就是它本身
- 最小生成树的边的权值之和总是唯一的
- 最小生成树的边数 = 顶点数-1
1.4.1.3 算法
1.4.1.3.1 Prim算法
不断通过最小的边 加入新点和新边,直到包括所有的点

当带权连通图的任意一个环中所包含的边权值不同时,最小生成树是唯一的
1.4.1.3.2 Kruskal算法
按权值的递增次序选择合适的边来构造最小生成树【不以自我为中心】

1.4.2 最短路径
1.4.2.1 BFS求无向图单源最短路径
从一点出发,通过BFS的visit,不断记录对应点的最短路径长度d[]和前驱结点path[]

1.4.2.2 Dijkstra求有向图单源最短路径
不断加入最近的点,判断当前抵达所有结点的最短路径长度。

1.4.2.3 Floyd求任意两点最短路径
每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短
A
(
0
)
A^{(0)}
A(0)允许有一个中间结点
v
0
v_0
v0
A
(
1
)
A^{(1)}
A(1)允许有两个中间结点
v
0
v_0
v0,
v
1
v_1
v1

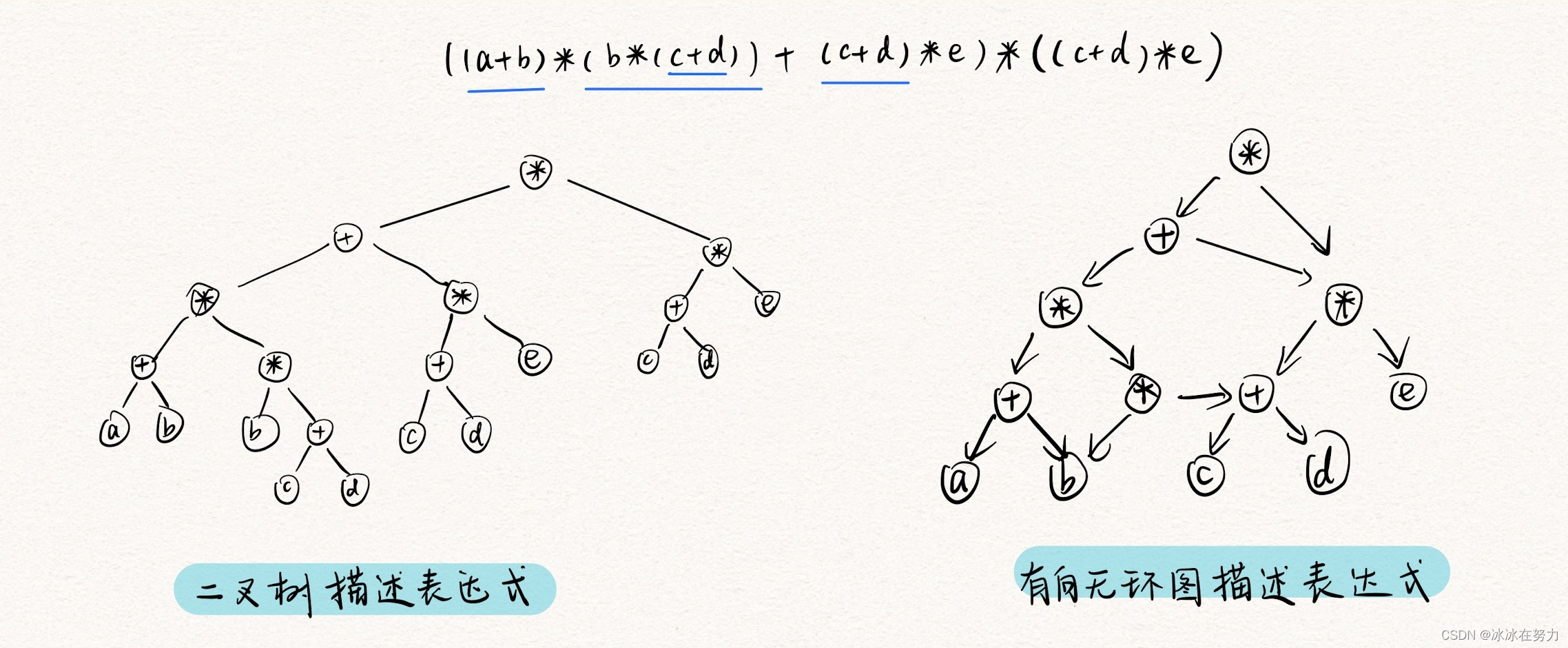
1.4.3 有向无环图描述表达式
若一个有向图中不存在环,则称为有向无环图,简称DAG图
1.4.4 拓扑排序

- 采用邻接矩阵存储,时间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2)
- 采用邻接表存储,时间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O(∣V∣+∣E∣)
1.4.5 逆拓扑排序

1.4.6 关键路径
- 计算最早开始时间和最晚开始时间
- 关键路径是指权值之和最大而非边数最多的路径
- 无论存在一条或是多条关键路径,增加任一关键活动的时间都会延长工程的工期
- 只有一条关键路径的时候,减少关键活动的时间会缩短工程的工期
- 有多条关键路径的时候,减少关键活动的时间不一定会缩短工程的工期
- 求关键路径的快速方法:找起点到终点的最长路径
AOE网:

计算过程:









 本文详细介绍了图的基本概念,包括图的定义、无向图与有向图、连通图和强连通图、生成树与生成森林等。深入探讨了图的存储方式如邻接矩阵、邻接表、十字链表和领接多重表,并讲解了深度优先搜索DFS和广度优先搜索BFS。此外,还讨论了图的应用,如最小生成树的Prim和Kruskal算法、最短路径问题及拓扑排序等。
本文详细介绍了图的基本概念,包括图的定义、无向图与有向图、连通图和强连通图、生成树与生成森林等。深入探讨了图的存储方式如邻接矩阵、邻接表、十字链表和领接多重表,并讲解了深度优先搜索DFS和广度优先搜索BFS。此外,还讨论了图的应用,如最小生成树的Prim和Kruskal算法、最短路径问题及拓扑排序等。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










