交换排序 快速排序 冒泡排序

交换排序

1. 基本思想

基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排
序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

---

2. 冒泡排序

这边查看我往期制作的冒泡排序，有很完整的排序过程。

往期冒泡瞬移区，请点我

---

3. 快速排序 · 升序(递归)

快速排序有几个比较热门的版本，我这边介绍三种 ：

1.hoare版本

2.挖坑版本

3.前后指针版本。

---

3.1 hoare版本

3.1.1 动图

---

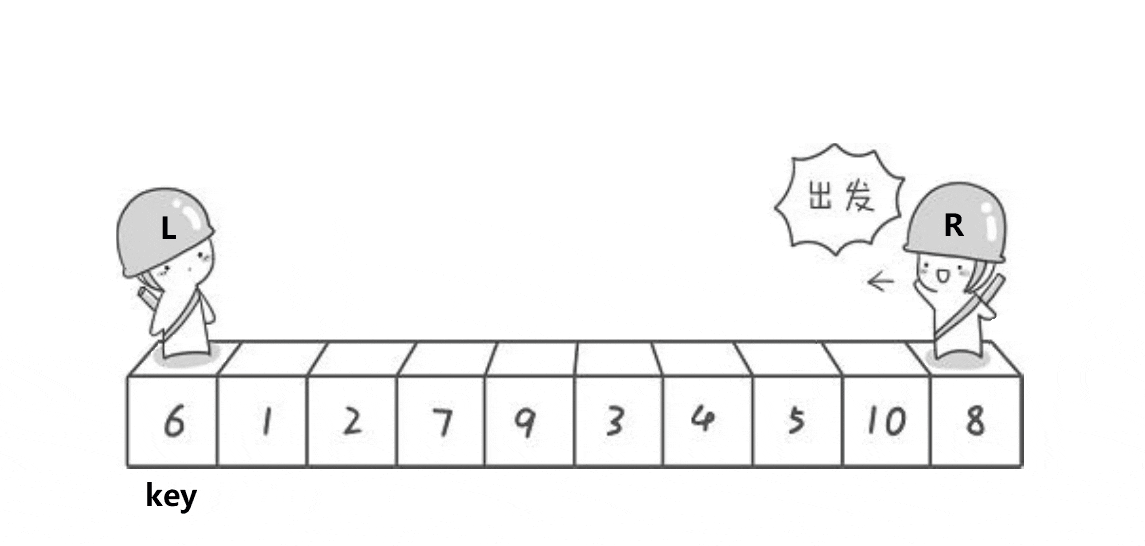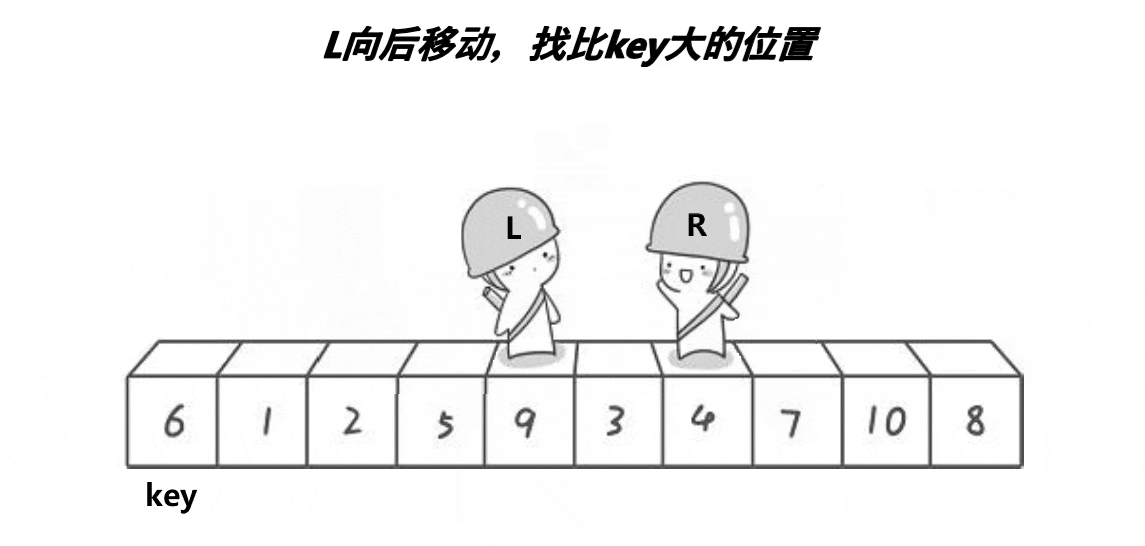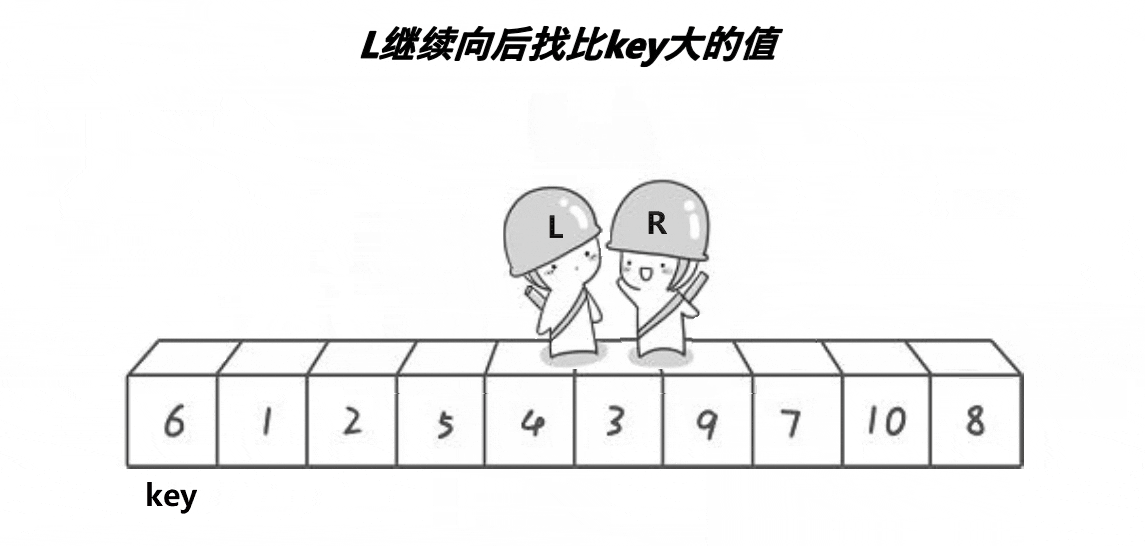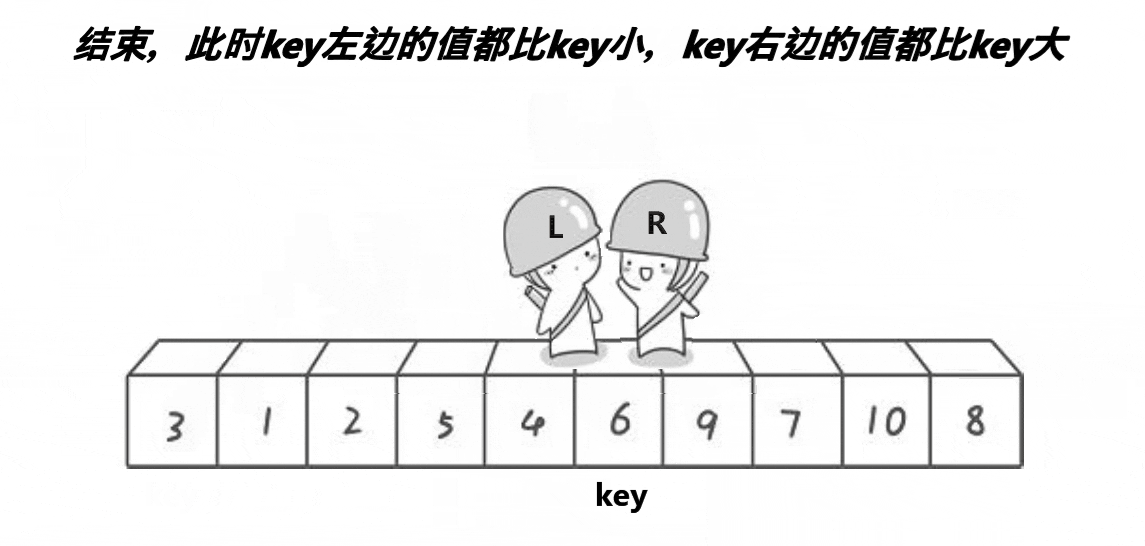
3.1.2 思想（配合动图理解）

我们首先选择一个key值作为基准（这里选择第一个值当），用两个指针left，right，begin，end。left和begin都指向第一个元素，right和end都指向末尾元素。

先让right走，right走到比key小或等于key的地方停下，然后left走，走到比key大的地方停下，最后交换left和right指向的值的位置。

途中如果left遇到right，则交换left（或right，都指向同个位置）和key指向元素的位置，跳出循环，这样单趟排序就完成了。接着开始递归了，将数据分为3份，[begin , key-1] key [key + 1 , end]（就是以key为分界线，将key左侧和右侧递归），将[begin , key-1] 和 [key + 1 , end] 递归。这样子单次递归就完成了，我们会发现key（交换后）左边全部会比key小，key右边会比key大。通过不断递归，一直左边比右边大，就完成了排序。

---

3.1.3 图文详解

我们就拿这个数组剖析。

left，key，begin指向第一个元素，right和end指向末尾元素。

我们让right先走（注意一定要让key另一边的先走,不然会出问题）,找到<=key或者与left相遇停下。这里是遇到了<key的停下。

然后到left移动，找>key或者与right相遇停下。这里找到7 比key小。

交换left和right指向元素的位置。

继续，right走。

left走。

交换left和right指向元素的位置。

right走，right遇到了left停下。

交换left和key指向元素的位置。

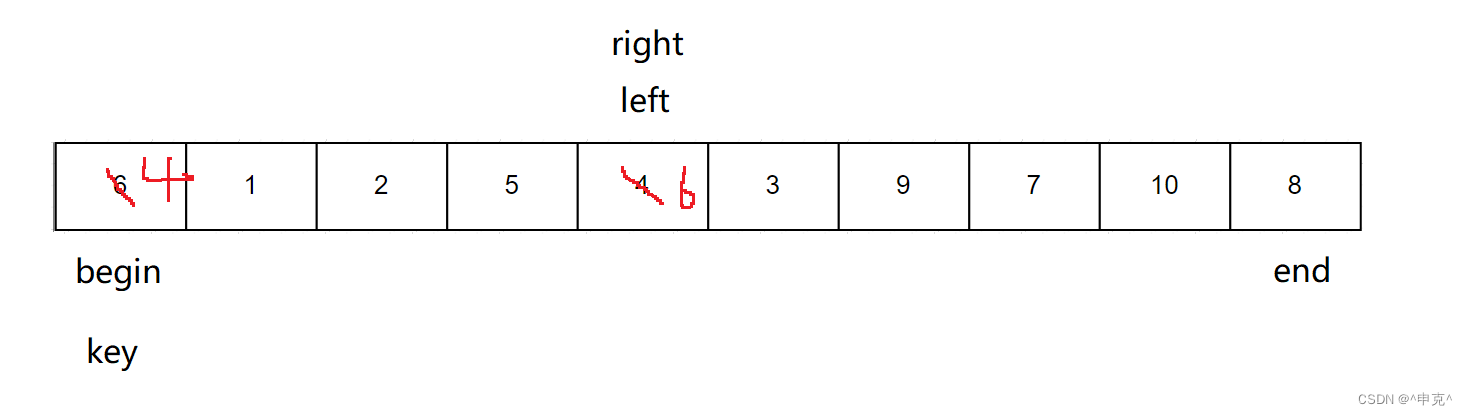
这样循环一轮后，原key（6）的左边比6小，原key（6）的右边比6大。

接着，开始递归把left的左边和left右边分别递归，继续排序。

大概步骤上面已经描述过了，我这边只展示左侧。

一切照旧，第一个元素给到left和begin，最后一个元素给到right和end。因为这里出现指针递归后再次使用的情况，所以我们在给指针赋值的时候，不能只考虑单次，特别是给left赋值。

一样right先走，然后到left走，left相遇到right。

交换位置。

递归。

right走，遇到left，交换left和key的值。

递归进来后，会发现只有一个元素（出现left == right的情况）或者没有元素，这种时候就不要进行任何操作，直接返回。

这样一边的排序就完成了。

---

3.1.4 代码

//交换
void Swap(int* left, int * right)
{
	int tmp = *left;
	*left = *right;
	*right = tmp;
}


//快速排序key法
void PartSort1(int* a, int left, int right)
{
	//只有一个元素返回
	if (right - left <= 1)
		return;

	int begin = left;
	int end = right;

	//将第一个元素定为keyi
	int keyi = left;

	while (left <right)
	{
		//单趟
		//让right先走，直到right<=keyi才停或者遇到left
		while (left != right && a[right] > a[keyi])
			right--;
		//right走完到left走，直到left遇到>keyi才停下来或者遇到right
		while (left != right && a[left] <= a[keyi])
			left++;

		//不相遇，交换左右
		if (left != right)
		{
			Swap(&a[left], &a[right]);
		}
		else //相遇交换left和keyi
		{
			Swap(&a[left], &a[keyi]);
			break;
		}
	}

	//[left, keyi - 1] keyi		[keyi +1, right]

	PartSort1(a, begin,left-1);
	PartSort1(a, left+1, end);
}

---

3.2 挖坑版本

3.2.1动图

---

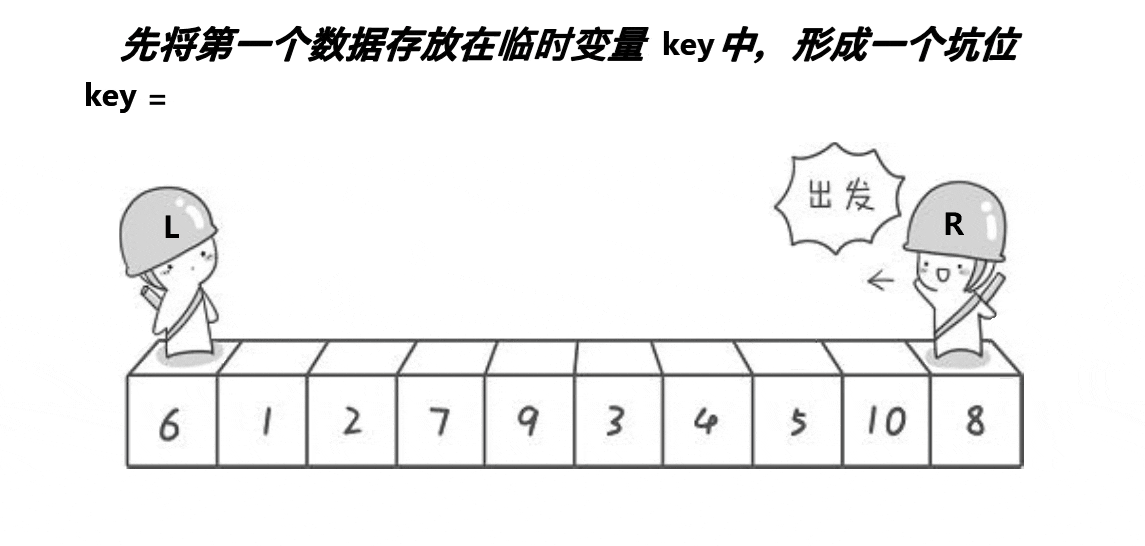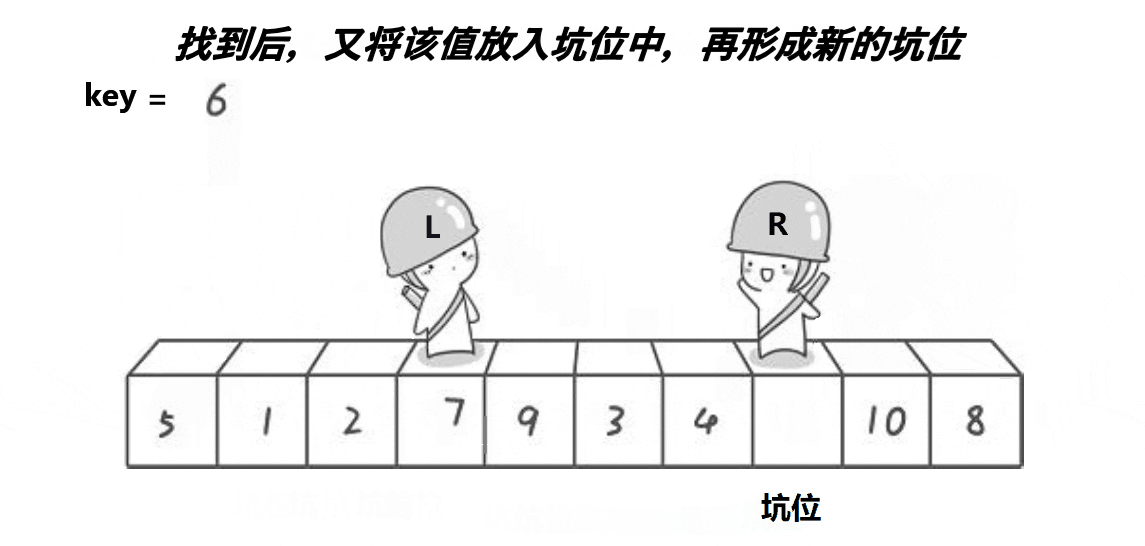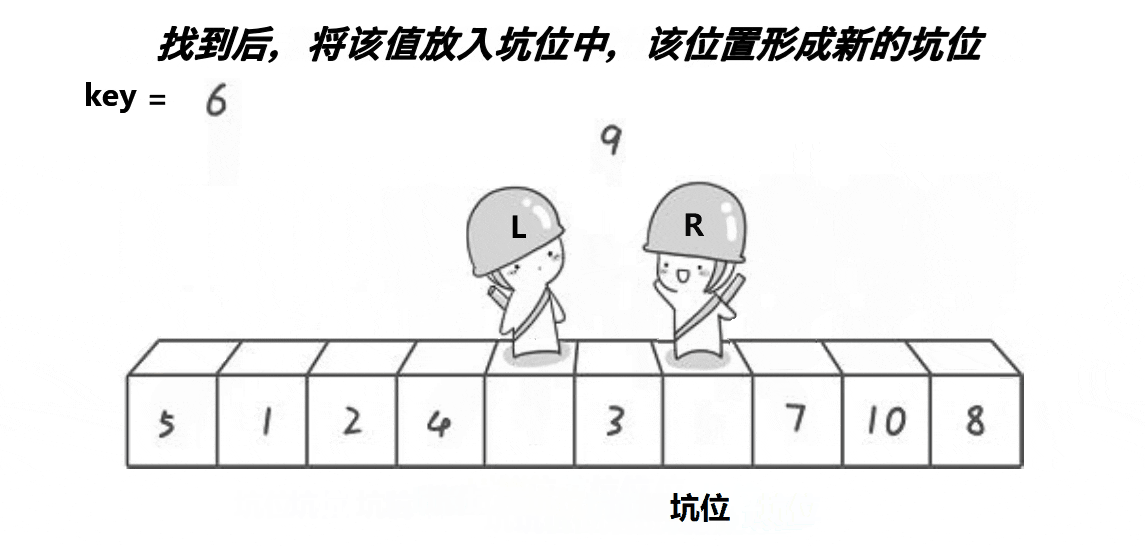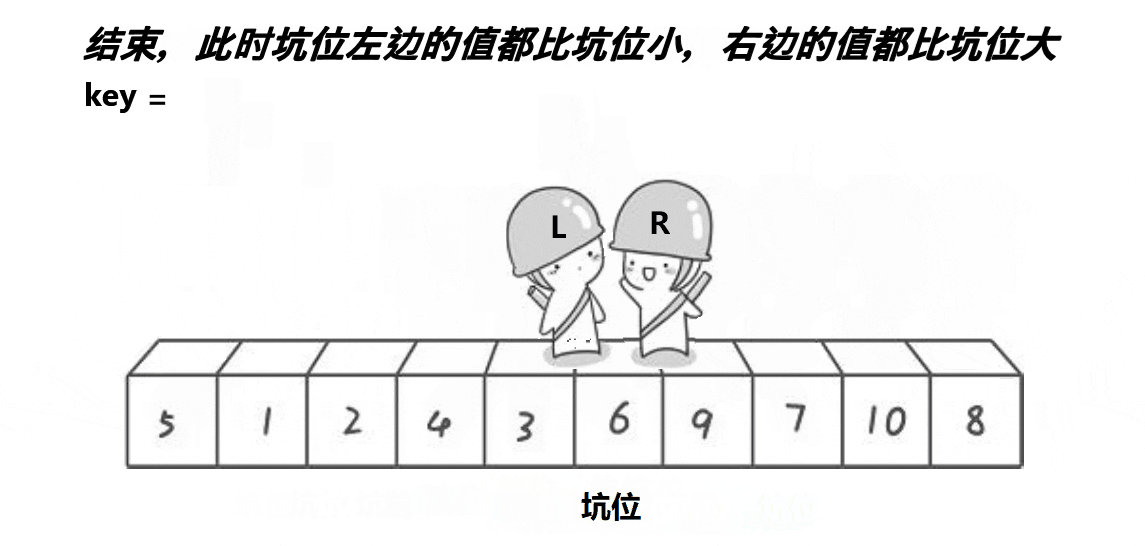
3.2.2 思想（配合动图理解）

其实挖坑版本本质是和hoare版本（key法）时候相同的。同样是right先走找小，left后走找大。不同的是它提前将key的值存起来，left和right在走到符合条件的状况时，采取的是将指向的元素赋值给另一个指针，自己就变成了坑位，最后相遇将存起来的key值给到坑位。递归也是相同的。

---

3.2.3 代码

//快速排序挖坑法
void PartSort2(int* a, int left, int right)
{
	//只有一个元素返回
	if (right - left <= 1)
		return;

	int begin = left;
	int end = right;

	//key存储初始坑位值
	
	int key = a[left];
	int hole = left;

	while (left < right)
	{
		//单趟
		//让right先走，直到right<=keyi才停或者遇到left
		while (left != right && a[right] > key)
			right--;

		//让right变成hole
		if (left != right)
		{
			a[hole] = a[right];
			hole = right;
		}
		else
			break;

		//right走完到left走，直到left遇到>keyi才停下来或者遇到right
		while (left != right && a[left] <= key)
			left++;

		if (left != right)
		{
			a[hole] = a[left];
			hole = left;
		}
		else
			break;

	}

	//这里就相遇了,坑位填上
	a[hole] = key;
	//[left, keyi - 1] keyi [keyi +1, right]

	PartSort1(a, begin, left - 1);
	PartSort1(a, left + 1, end);
}

---

3.3 前后指针版本

3.3.1 动图

---

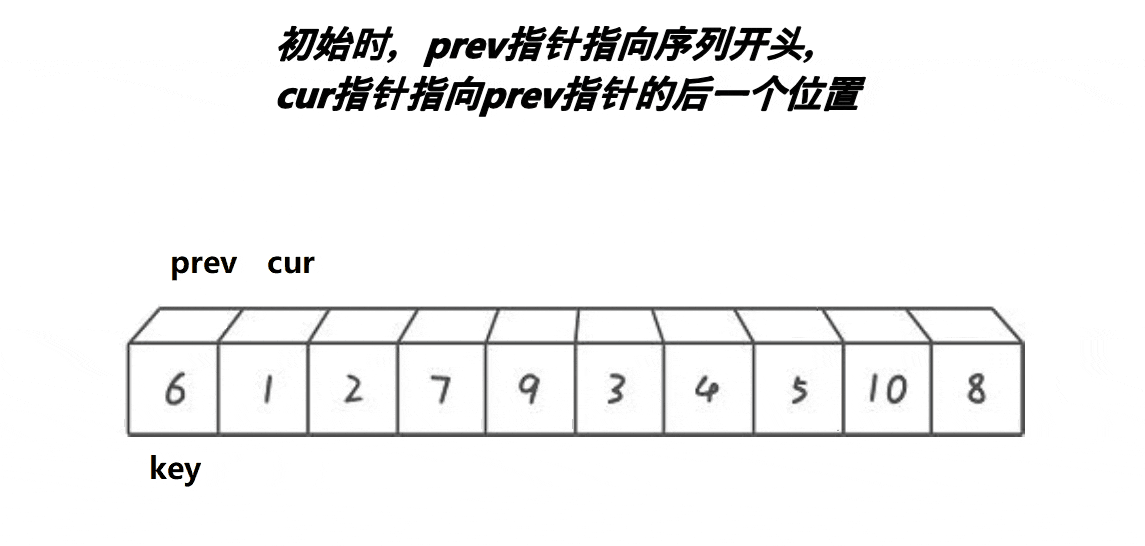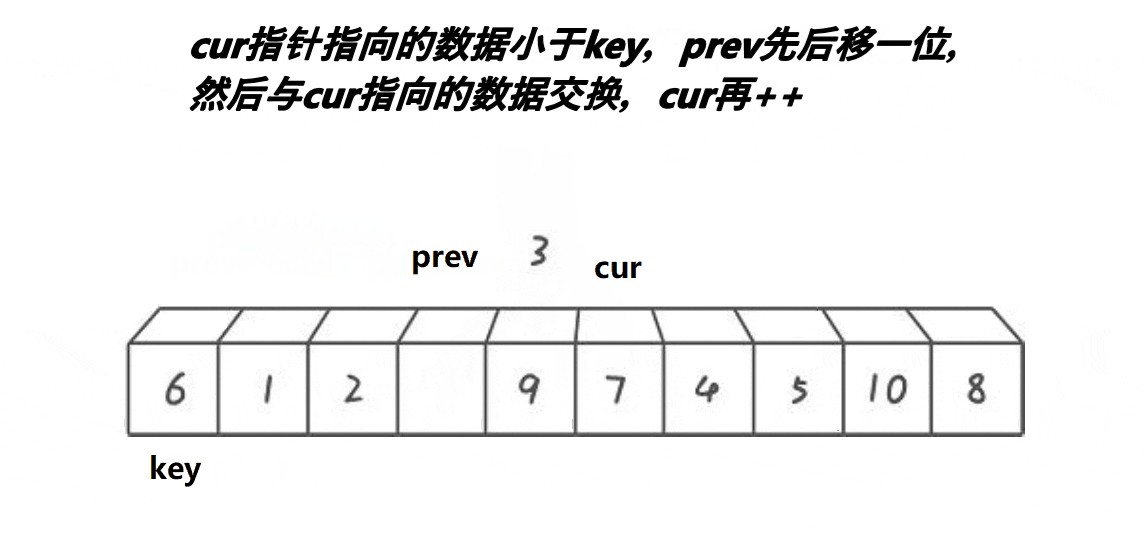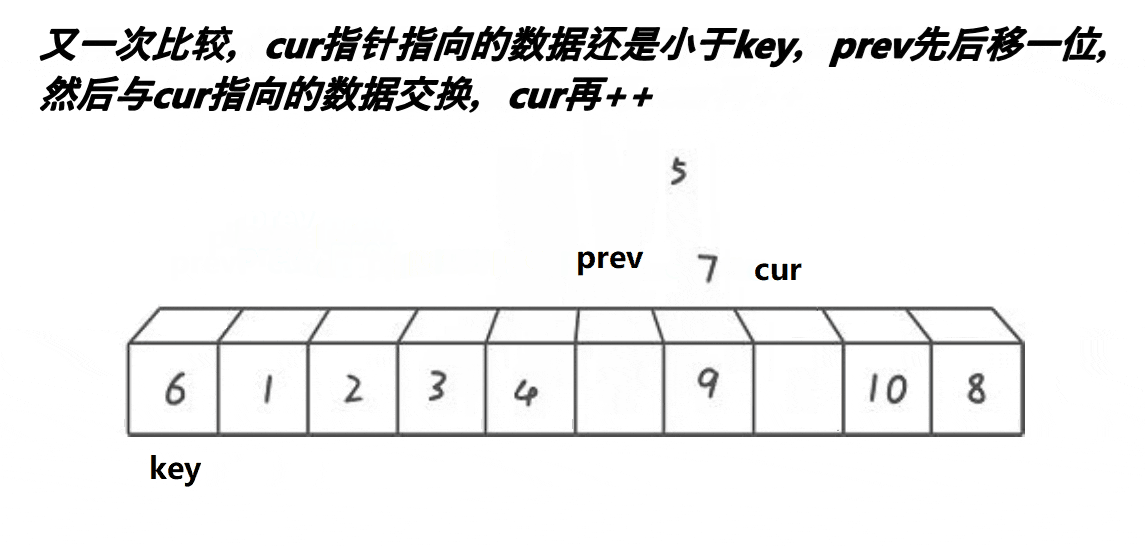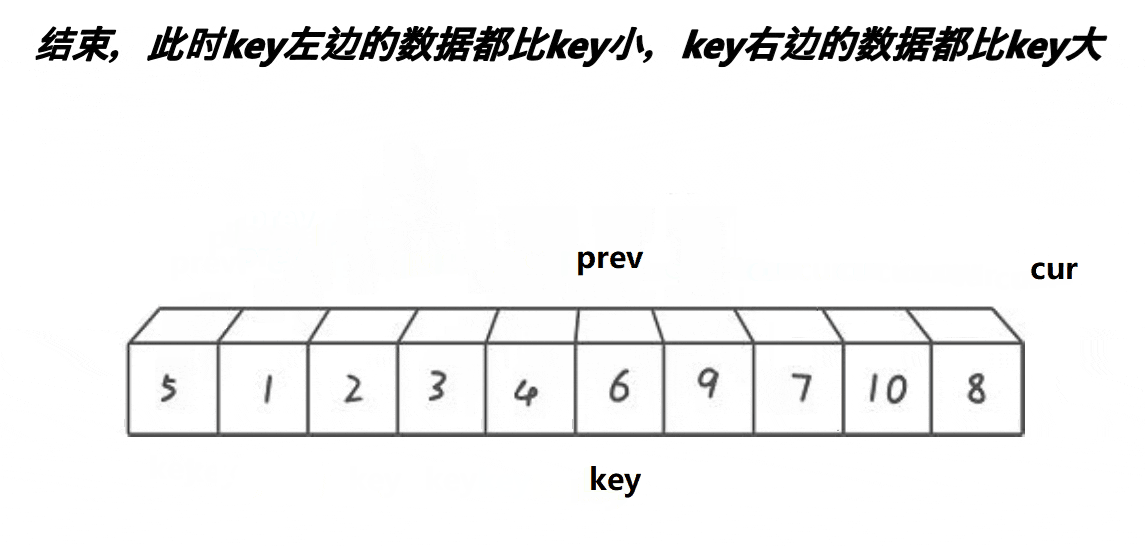
3.3.2 思想（配合动图理解）

同样，首先定义一个基准key（这里用首元素），利用两个指针prev和cur。cur去找比key小的值，prev在比key大的值的前面等候，只要cur符合情况，prev++，然后交换cur和prev指向元素的位置，不断重复直至cur到数据末尾，最后交换prev和key指向元素的位置，就完成单趟排序。其实这个思想不难理解，就是将比key大的值不断向后走，比key小的值不断向左走。prev后一个位到cur之间的值是大于key的，cur走到末尾了，就会变成[key] [比key小] [prev] [比key大] 这样组合，然后通过不断递归，小的在左边，大的在右边，最后也就完成了排序。

---

3.3.3 代码

//交换
void Swap(int* left, int * right)
{
	int tmp = *left;
	*left = *right;
	*right = tmp;
}


//快速排序前后指针法
void PartSort3(int* a, int left, int right)
{
	//只有一个元素返回
	if (right - left < 1)
		return;

	//三数取中
	//int mid = (left + right) / 2;
	//selectKey(&left, &right, &mid);

	int key = left;
	int prev = left;
	int cur = left+1;

	//cur先找到第一个比key大的值
	while (cur <= right && a [cur] <= a[key])
	{
		prev++;
		cur++;
	}

	while (cur <= right)
	{
		//然后cur找小于key的值,或者遇到
		while (cur <= right && a[cur] > a[key])
		{
			cur++;
		}
		if (cur > right)
			break;


		//交换prev+1和cur的位置
		prev++;
		Swap(&a[prev], &a[cur]);
		cur++;

	}

	//到这里cur已经跳出来了，交换key和prev的位置
	Swap(&a[key], &a[prev]);

	//a[key,prev-1] prev a[prev+1,cur-1]
	PartSort3(a, left, prev - 1);
	PartSort3(a,prev + 1, cur - 1);
}

---

3.4 一些小优化

快速排序其实是有点小弊端的，就是key值的选取。快速排序在面对一些比较有序的数组的时候，选出key值会比较极端（很大或者很小），也就是面临最坏情况的时候，他的时间复杂度是O(n^2)。所以我们可以对他采取一些小优化，如三数取中法，随机选key。

---

3.4.1 三数取中法

顾名思义，就是取三个数字折中选取。这样key值成为极端数的概率会变小很多，效率也就提高了。

int SelectMidKey(int* a, int begin, int end)
{
	int mid = begin + (end - begin) / 2;
	if (a[begin] < a[mid])
	{
		if (a[mid] < a[end])
			return mid;
		else
		{
			if (a[begin] > a[end])
				return begin;
			else
				return end;
		}
	}
	else
	{
		if (a[mid] > a[end])
			return mid;
		else
		{
			if (a[begin] < a[end])
				return begin;
			else
				return end;
		}
	}
}

---

3.4.2 随机选取法

随机选取法，就是在这组数据中随机选择一个数当做key值。这也是一种方法，但随机也有概率选取最大或者最小的值，所以往往大多数会用三数取中。

---

4. 时间和空间复杂度

4.1 快速排序时间复杂度

O(n * log n) 。
最坏情况是O（n^2），当我们key值选择最数据中最大或者最小的情况。

4.2 快速排序空间复杂度

快排空间用于递归嘛，递归一次空间就得增加，也就是O(n * log n)。
最坏情况如上，O(n^2)。