动手学深度学习---学习过程（第三章-线性神经网络）_推导出使用平方误差的线性回归优化问题的解析解。为了简化问题,可以忽略偏置-优快云博客

本文链接：https://blog.youkuaiyun.com/m0_65472749/article/details/144947854

3.1线性回归

练习1：
在这里插入图片描述
1.1

1.2最小化均方误差等价于对线性模型的极大似然估计。

练习2：推导出使用平方误差的线性回归优化问题的解析解。为了简化问题，可以忽略偏置（我们可以通过向添加所有值为1的一列来做到这一点）。
2.1用矩阵和向量表示法写出优化问题（将所有数据视为单个矩阵，将所有目标值视为单个向量）。
2.2计算损失对的梯度。
2.3通过将梯度设为0、求解矩阵方程来找到解析解。
2.4什么时候可能比使用随机梯度下降更好？这种方法何时会失效？

①
在这里插入图片描述
②

③

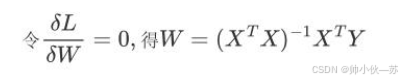
④

练习3：

不会

3.2. 线性回归的从零开始实现

练习1：如果我们将权重初始化为零，会发生什么。算法仍然有效吗？
在本例当中，是有效的。
在“初始化模型参数”把w换成

w = torch.zeros(2,1,requires_grad=True)

但是在一般的模型中：
①对称性破坏问题：在神经网络中，权重的初始化非常重要。如果所有权重都初始化为零，那么每一层的所有神经元在前向传播和反向传播时都会得到相同的梯度更新。这意味着所有神经元在训练过程中将变得相同，无法学习到不同的特征，从而导致模型无法有效地进行学习。

②梯度更新相同：当权重初始化为零时，反向传播中的梯度计算也会受到影响。如果所有权重为零，所有神经元的梯度也会相同，这使得每个神经元的更新步伐相同，导致模型无法捕捉到多样的特征。因此，网络的每一层和每一个神经元将会表现得一样，最终无法学习到有用的特征表示。

③无法打破对称性：神经网络通常依赖于随机初始化来打破对称性，使得每个神经元能够在训练过程中学习到不同的特征。如果权重全都初始化为零，这种对称性就没有被打破，训练过程中的每个神经元将无法有不同的输出，导致模型无法有效区分输入数据的不同特征。
练习2：假设试图为电压和电流的关系建立一个模型。自动微分可以用来学习模型的参数吗?
在“生成数据集”将电流当作features,电压当作labels。
练习3：能基于普朗克定律使用光谱能量密度来确定物体的温度吗？
在这里插入图片描述
根据公式反推T的公式。

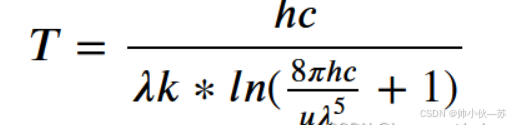
练习4：计算二阶导数时可能会遇到什么问题？这些问题可以如何解决？
计算二阶导数在神经网络中面临许多挑战，主要是由于高计算开销、数值不稳定性、高维问题以及存储复杂度等原因。为了应对这些问题，通常采用近似方法（如L-BFGS、自然梯度法）、正则化、梯度裁剪、分布式计算等技术。这些方法能够有效地减少计算和存储的复杂性，帮助神经网络在高维和大规模数据集的情况下依然能够进行有效的优化。
练习5：为什么在squared_loss函数中需要使用reshape函数？
为了使y 和y_hat的形状一致，从而完成运算。
练习6：尝试使用不同的学习率，观察损失函数值下降的快慢。
学习率如果过大，则损失函数值会发生来回波动；学习率如果太小则损失函数值下降很慢。
练习7：如果样本个数不能被批量大小整除，data_iter函数的行为会有什么变化？
①丢弃最后一个不完整批次
②保留最后一个较小批次
都有可能，但是根据本书的例子来说，是会保留较小批次的。
但是如何丢弃最后一个不完整批次呢？

#练习7如何处理不完整批次？
from torch.utils.data import DataLoader, TensorDataset
def data_iter(batch_size, features, labels):
    num_examples = len(features)  #长度
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)#对列表（list）进行原地随机打乱。
    dataloader = DataLoader(indices, batch_size=batch_size, drop_last=False)

    for batch in dataloader:
        print(batch)
        yield features[batch], labels[batch]
        #yield 是一个关键字，它用于在函数中生成一个生成器（generator）。
        #生成器是一个特殊类型的迭代器，可以在遍历过程中动态地生成数据，而不是一次性将所有数据加载到内存中。这对于处理大型数据集时非常有用，可以提高内存效率。
batch_size = 7
#print(len(features))
for X, y in data_iter(batch_size, features, labels): #和之前的for循环相联系，
    print(X, '\n', y)#只输出一次
    #break

只需要修改“drop_last=False”即可。

3.3. 线性回归的简洁实现

一些收获：
①在读取数据集中，TensorDataset函数的作用？
将一个或多个张量组合在一起。

#举例：
import torch
from torch.utils.data import TensorDataset, DataLoader

# 创建特征和标签张量
features = torch.tensor([[1, 2], [3, 4], [5, 6]])
labels = torch.tensor([0, 1, 0])

# 创建 TensorDataset
dataset = TensorDataset(features, labels)

# 加载数据
dataloader = DataLoader(dataset, batch_size=2)

# 遍历数据集
for data in dataloader:
    print(data)

#输出
[tensor([[1, 2],
         [3, 4]]), tensor([0, 1])]
[tensor([[5, 6]]), tensor([0])]

②DataLoader函数的作用？
DataLoader是为了简化并优化数据的加载过程,dataset是数据集的核心，batch_size是每次迭代时返回数据的样本数。shuffle表示是否随机打乱。

#举例
import torch
from torch.utils.data import DataLoader, TensorDataset

# 假设你有一个输入特征和标签
inputs = torch.tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0], [7.0, 8.0]])
labels = torch.tensor([0, 1, 0, 1])

# 使用 TensorDataset 打包输入和标签
dataset = TensorDataset(inputs, labels)

# 创建 DataLoader
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)

# 使用 DataLoader 迭代数据
for batch_inputs, batch_labels in dataloader:
    print("Inputs:", batch_inputs)
    print("Labels:", batch_labels)

#输出
Inputs: tensor([[1., 2.], [5., 6.]])
Labels: tensor([0, 0])
Inputs: tensor([[3., 4.], [7., 8.]])
Labels: tensor([1, 1])

在本代码中，如果将shuffle设置为true，即打乱顺序，具有随机性，即可能每次输出都不一样。
但如果设置为false，即输出一样了。

③next函数的作用？
next() 函数从一个迭代器中获取下一个元素。其中next的参数是iterator

#举例
import torch
from torch.utils.data import DataLoader, TensorDataset

# 创建一些示例数据
inputs = torch.tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0], [7.0, 8.0]])
labels = torch.tensor([0, 1, 0, 1])

# 创建TensorDataset
dataset = TensorDataset(inputs, labels)

# 创建DataLoader
dataloader = DataLoader(dataset, batch_size=2, shuffle=False)

# 获取迭代器
iterator = iter(dataloader)

# 使用next获取下一个批次
batch1 = next(iterator)
print(batch1)

# 获取下一个批次
batch2 = next(iterator)
print(batch2)

#输出
[tensor([[1., 2.],
         [3., 4.]]), tensor([0, 1])]
[tensor([[5., 6.],
         [7., 8.]]), tensor([0, 1])]

练习1：如果将小批量的总损失替换为小批量损失的平均值，需要如何更改学习率？
问法有问题，代码本来就是平均值。
计算均方误差使用的是MSELoss类，也称为平方范数。默认情况下，它返回所有样本损失的平均值。
所以问法可以变为如果将平均值损失替换为总损失，需要如何更改学习率？
学习率除batch_size即可
练习2：查看深度学习框架文档，它们提供了哪些损失函数和初始化方法？用Huber损失代替原损失，即
在这里插入图片描述
MeanLoss替换为SmoothL1Loss即可
练习3：如何访问线性回归的梯度？
可以放在for循环里面计算每一步的梯度
print(net[0].weight.grad)

num_epochs = 3
for epoch in range(num_epochs):
    for batch ,(X, y) in enumerate(data_iter): #enumerate是用来获得可迭代对象的函数
        l = loss(net(X) ,y)
        #print(f'batch {batch+1},loss {1:f}')
        trainer.zero_grad()
        l.backward()
        print(net[0].weight.grad)
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')