机器学习 - 分类 逻辑回归 Logistic Regression（学习笔记）

逻辑回归设计思路

乍一看算法名字，会认为逻辑回归是用来解决“回归问题”的算法，但其实它是针对“分类问题”的算法。

前面我们知道，线性回归是基于样本数据拟合出一个可以预测数值的模型，从而实现了回归。而通过连续型数值获取离散型数值是很容易的，这正如水龙头喷出的水过于集中一样，只要加个转换器(花洒)就可以使水流分散输出。

19 世纪统计学家皮埃尔·弗朗索瓦·韦吕勒发明了 Logistic 函数，该函数的叫法有很多，比如在神经网络算法中被称为Sigmoid函数，也有人称它为 Logistic 曲线。该函数图像的数学表达式如下：
 

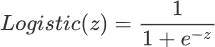
其函数图像如下所示：相当于把得分值转换成概率值。

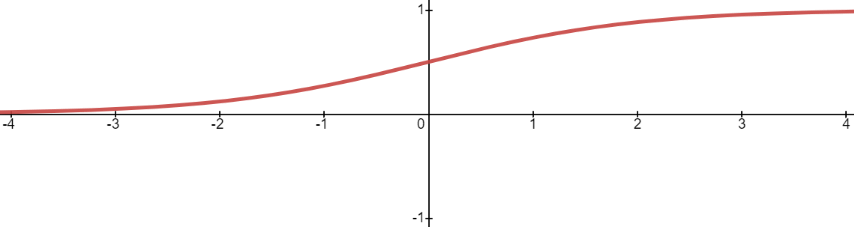
Logistic 函数也称为 S 型生长曲线，取值范围为 (0,1)，它可以将一个实数映射到 (0,1) 的区间，非常适合做二元分类。当 z=0 时，该函数的取值为 0.5，随着 z 的增大，对应的函数值将逼近于 1；而随着 z 的减小，其函数值将逼近于 0。
对于 Logistic 函数而言，坐标轴 0 是一个有着特殊意义坐标，越靠近 0 和越远离 0 会出现两种截然不同的情况：任何