K-Means聚类算法：从原理到实践

---

---

前言

在机器学习和数据挖掘领域，聚类算法是一种重要的无监督学习方法，用于将数据集中的样本划分为若干个簇，使得同一簇内的样本相似度高，而不同簇之间的样本相似度低。K-Means算法是其中最经典且广泛应用的聚类算法之一。本文将详细介绍K-Means算法的原理、实现步骤、优缺点以及实际应用场景。

一、K-Means算法简介

K-Means算法是一种基于距离的聚类算法，由J. MacQueen在1967年提出。其核心思想是通过迭代优化，将数据集划分为K个簇，使得每个簇内的样本点到簇中心的距离最小化。

1.基本概念

• 簇（Cluster）：一组相似的数据点的集合。

• 簇中心（Centroid）：簇内所有数据点的均值，代表该簇的中心位置。

• 距离度量：通常使用欧氏距离来衡量数据点之间的相似性。

二、K-Means算法步骤

1.K-Means算法分为以下几个步骤：

• 初始化：随机选择K个数据点作为初始簇中心。
• 分配数据点：计算每个数据点到K个簇中心的距离，并将其分配到距离最近的簇。
• 更新簇中心：重新计算每个簇的中心，即簇内所有数据点的均值。
• 迭代优化：重复步骤2和步骤3，直到簇中心不再发生变化或达到最大迭代次数。

三、K-Means算法的Python实现

处理一个洋酒品牌的数据：

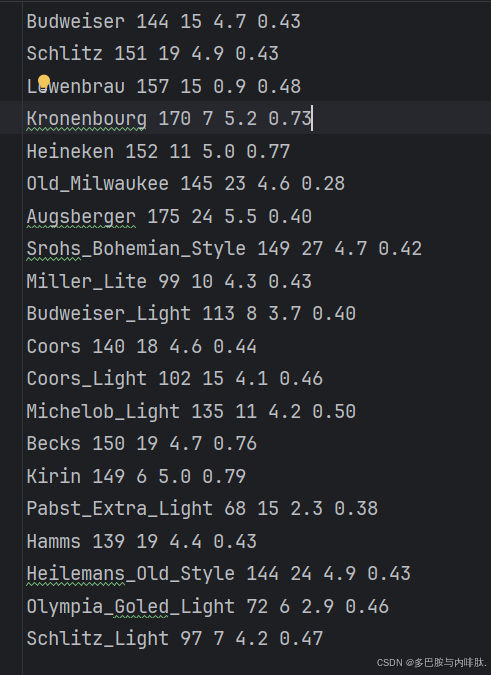
1.预处理：

import pandas as pd
from sklearn.cluster import KMeans
from sklearn import metrics
import matplotlib.pyplot as plt

#读取文件
beer = pd.read_table('数据/data.txt', sep=' ')
#传入变量（列名）
X = beer[['calories','sodium','alcohol','cost']]

2.分成不同的簇，自动计算轮廓系数得分：

scores = []
for k in range(2,10):
    lables = KMeans(n_clusters=k).fit(X).labels_#从左到右依次计算
    score = metrics.silhouette_score(X, lables)#轮廓系数
    scores.append(score)
print(scores)

3.绘制得分结果:

plt.plot(list(range(2,10)),scores)
plt.xlabel('Number of Clusters Initialized')
plt.ylabel('Sihouette Score')
plt.show()

4.聚类:

km = KMeans(n_clusters=2).fit(X) #K值为2【分为2类】
beer['cluster'] = km.labels_

5.对聚类结果评分：

score = metrics.silhouette_score(X,beer.cluster)#X:数据集,scaled_cluster:聚类结果
print(score)#score:非标准化聚类结果的轮廓系数```

输出结果：

四、K-Means算法的优缺点

1 优点

• 简单高效：算法原理简单，易于实现，计算效率高。
• 可扩展性强：适用于大规模数据集。
• 广泛应用：可用于图像处理、市场细分、文档分类等多个领域。

2 缺点

• 需要预设K值：K值的选择对结果影响较大，且通常需要人工指定。
• 对初始值敏感：初始簇中心的选择可能导致不同的聚类结果。
• 对噪声和异常值敏感：噪声数据可能影响簇中心的计算。
• 仅适用于凸数据集：对于非凸形状的数据集，K-Means效果较差。

总结

K-Means算法作为一种经典的聚类算法，因其简单、高效的特点，在实际应用中得到了广泛的使用。然而，它也存在一些局限性，例如对初始值敏感、需要预设K值等。在实际使用中，可以结合其他方法（如K-Means++初始化、肘部法选择K值等）来优化算法的性能。

数据文件发评论区了！！！