Shamir门限方案的秘钥分享（不要求支持大数）

Shamir门限方案的秘钥分享（不要求支持大数）

题目描述

【实验目的】

1) 通过基于Shamir门限方案的密钥分割及恢复的演示，理解密钥分割的重要性，理解密钥分割的基本原理和作用，掌握基于Shamir门限方案的密钥分割软件的使用

【实验原理】

秘密共享体制为将秘密分给多人掌管提供了可能。例如重要场所的通行、遗嘱的生效等都必须由两人或多人同时参与才能生效，这时都需要将秘密分给多人掌管并同时参与才能恢复。在实际应用中，秘密共享的要求多种多样、形形色色，每一种解决问题的方案都可成为一种体制。1979年，Shamir在提出秘密分享思想的同时，利用拉格朗日插值多项式理论设计出了一个具体的（t,n）秘密分享方案。1979年以后，人们通过对秘密共享问题的分析研究，构建出了许多类型的秘密共享体制。具有代表性和一般性的除了有Shamir提出的(t,n)门限体制，还有Blakley提出的矢量体制，Asmuth和Bloom提出的同余类体制，Karnin提出的矩阵法体制等。

一般地，一个由秘密分发者D和参与者P1，P2，…，Pn构成的（t,n）秘密分享体制包含下面两个协议：

（1） 秘密分发协议：在这个协议中，秘密分发者D在n个参与者中分享秘密s，每个参与者Pi获得一个碎片si，i=1,2，…，n。

（2） 秘密重构协议：在这个协议中，任意不少于t个参与者一起合作，以自己的碎片为输入，重构原秘密s。

一个安全的（t,n）秘密分享体制必须同时提供两个性质：一方面，任意t个参与者通过提供自己的碎片能够协作地恢复出原秘密s；另一方面，任意少于t个参与者即便拥有自己的碎片也无法计算关于原秘密s的任何信息。一般称这里的t为门限值。

Shamir提出的基于LaGrange插值公式的密钥分存思想是,利用有限域GF(p)上的t-1次多项式

h(x)= at- 1xt- 1+ … + a1x+ a0 mod p (1)

构造秘密共享的（t,n）门限体制。其中，所选的随机素数p要大于最大可能的秘密数S和参与者总数n，并且公开；S=h(0)=a0，而at-1，at-2，… ，a1为选用的随机系数，这些都需要保密，在生成n个秘密份额之后即可销毁。通过计算多项式h(x)对n个不同xi的取值就给出每个人的秘密份额:

Si= h(xi)mod p，i= 1,2,3,… ,n (2)

每一(xi,Si)对就是曲线h上的一个点，可看作是用户的标识符。由于任意t个点都可唯一地确定相应的t- 1次多项式，所以，秘密S可以从t个秘密份额重构。给定任意t个秘密份额Si1，Si2，… ，Sit，由LaGrange插值公式重构的多项式为

具体步骤如下。如图所示

其中    需要使用到逆元计算；

关于逆元，可以参看逆元（数论中的倒数）_淼润淽涵的博客-优快云博客其中有些例子不够完善，请谨慎选取，小心验证。

具体例子：

n=5, t=3, p=17; 随机选取K=13,a1=10,a2=2;

于是有

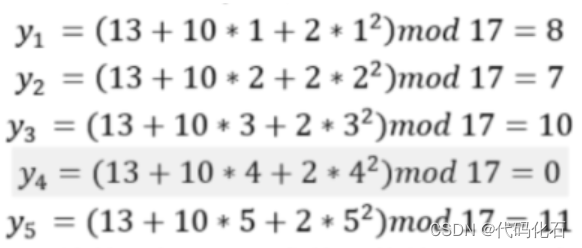
解密的时候选取  （1 8）（2 7） （5 11）来解密

上面的例子每个倒数都计算了一次逆元，大家可以想想有没有什么简化的方法。

输入

大素数p

子秘钥总数n

门限值t

输出

设置的密钥与恢复的密钥的差值

 代码

import random
import math


# 输入p, w, t, s 程序入口
def runCode(predefineData):
    p = 0
    w = 0
    t = 0
    s = 0
    if not predefineData:
        tempstr = input()
        p = int(tempstr)
        p = testPrimality(p)

        w = input()
        t = input()

        if (int(w) >= int(t)):
           
            s = 13
            
        else:
            
            runCode([])
        predefineData = [w, t, p, s]
    else:
        w = predefineData[0]
        t = predefineData[1]
        p = predefineData[2]
        s = predefineData[3]

    a = generatesubKey(t, w, s, p)  # 生成子密钥
    generateMainKey(s, p, t, a)  # 求解主密钥


# 生成子密钥
def generatesubKey(t_str, w_str, s, p):
    a_j = [0]  # 存放多项式系数列表
    x_i = [0]  # 多项式x取值列表

    t = int(t_str)
    w = int(w_str)

    x_i = randomList(1, w, w, True)  # 获取x 不相同
    a_j = randomList(1, 5, t - 1, False)  # 多项式参数

    x_i.sort()  # 升序排列x
   

    subKey = {}  # 子密钥字典

    for i in range(0, w):
        polynomialSum = s;  # 多项式求和
        x = x_i[i]
        for j in range(0, t - 1):
            a = a_j[j]
            polynomialSum += (a * math.pow(x, j + 1))

        regsubK = polynomialSum % p  # 得到其中一个子密钥
        subKey[x] = int(regsubK)  # 添加到密钥字典
        
    return subKey




# 生成主密钥
def generateMainKey(s, p, t,a):
    x_list = []
    y_list = []
    subSet = a  # 输入密钥
    recoveredS = 0
    # 遍历输入密钥字典 生成x y
    for key, value in subSet.items():
        x_list.append(key)
        y_list.append(value)
        #print("(" + str(key) + "," + str(value) + ")")

    # 生成解密表达式
    for i in range(0, len(x_list)):
        x_i = x_list[i]
        temp_j = 1
        for j in range(0, len(x_list)):
            if (j != i):
                x_j = x_list[j]
                temp_one = float(x_j) / (x_j - x_i)
                temp_j = temp_j * temp_one

        
        recoveredS += y_list[i] * temp_j
        

    recoveredS = int(round(recoveredS))  # 四舍五入 int
    recoveredS = recoveredS % p

    
    if recoveredS == s:
        print("0\n")
    else:
        print("解密失败\n")



# 检测素数
def testPrimality(p):
    temp = p;
    p = math.sqrt(p)
    p = int(p)
    for i in range(2, (p + 1)):
        f = temp / i
        if (f.is_integer()):
            newP = input("Enter prime number")
            newP = int(newP)
            newP = testPrimality(newP)
            temp = newP
            break
    return temp


# 得到一个随机数 state: true 不重复 false 可以重复
def getRandomNum(xlist, start, stop, state):
    # x_subi = []
    x = random.randint(start, stop)
    if state is True:
        if not x in xlist:
            return x
        else:
            x = getRandomNum(xlist, start, stop, state)
            return x
    else:
        return x


# 得到随机列表 state: true 不重复 false 可以重复
def randomList(start, stop, length, state):
    if length >= 0:
        length = int(length)
    start, stop = (int(start), int(stop)) if start <= stop else (int(stop), int(start))
    random_list = []
    for i in range(length):
        num = getRandomNum(random_list, start, stop, state)
        random_list.append(num)

    return random_list


# runCode(["5","3",11,5])
runCode([])