【LeetCode】654 and 1688（二叉树基础思想之递归算法2）

本篇文章内容为二叉树基础思想之递归算法1的延伸，有关其具体原理可参考链接下文章内容。

654. 最大二叉树

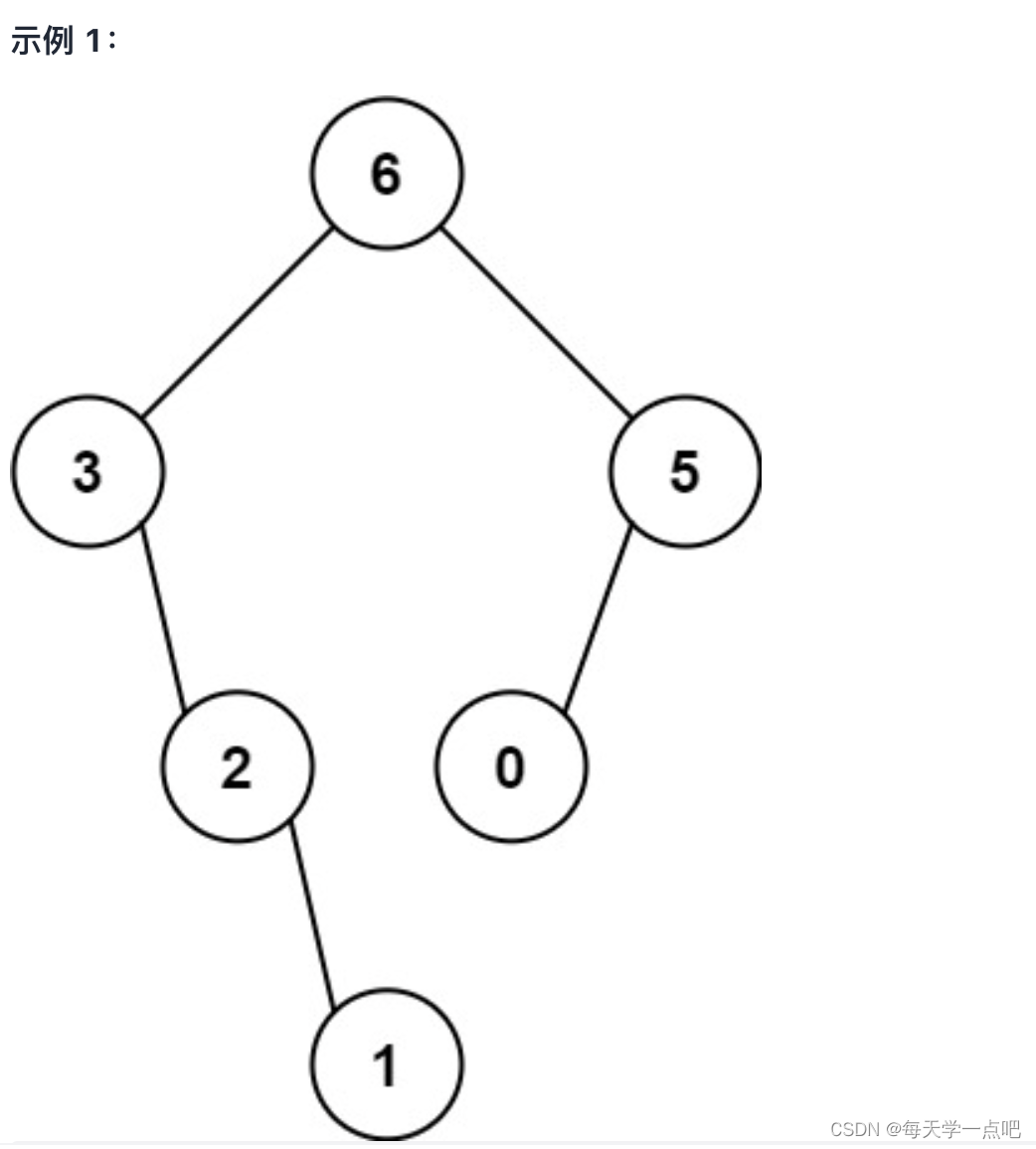
解法：递归
「该做什么」：找到当前数组（树）的最大值及其索引。
「什么时候做」：需先找到最大值索引，最大值索引左侧元素为其左子树，右侧元素为其右子树。因此是前序遍历框架。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:
        def build(left, right):
            if left >= right:
                return None
            value = float("-inf")
            _index = 0
            for i in range(left, right):
                if nums[i] > value:
                    value = nums[i]
                    _index = i
            node = TreeNode(value)
            node.left = build(left, _index)
            node.right = build(_index+1, right)
            return node
        return build(0, len(nums))

1688. 比赛中的配对次数

解法：递归模拟
该题同意可以抽象为树的遍历问题。需要明确下列内容：
「该做什么」：当前状态，比赛次数为count = n // 2，并对n进行更新，若为奇数 n=(n-1)//2 + 1，若为偶数，n = n // 2。
「什么时候做」：对n进行更新后，进入下一轮比赛。因此是前序遍历框架。
实际撰写代码过程中需注意终止条件为 n == 1，即只剩下一只队伍。

class Solution:
    def numberOfMatches(self, n: int) -> int:
        if n == 1:
            return 0
        count = n // 2
        if n % 2 == 0:
            n = n // 2
        else:
            n = (n-1) // 2 + 1
        count += self.numberOfMatches(n)
        # print(count)
        return count

总结

对上述递归问题的解决思路作出补充，除明确「该做什么」和「什么时候做」以外，还需要进行分析确定递归的终止条件是什么。例如654为数组为空，1688则为队伍数量为1。
其它类似思想题目可参考：
105. 从前序与中序遍历序列构造二叉树
106. 从中序与前序遍历序列构造二叉树