数字和字符串-优快云博客

本文链接：https://blog.youkuaiyun.com/m0_64141446/article/details/139382625

数组和字符串

1.数组简介

A 集合、列表和数组

①集合

集合的定义

由一个或多个确定的元素所构成的整体。

通俗来讲集合就是将一组事物组合在一起。

集合的特性

①集合里的元素类型不一定相同

（你可以将商品看作一个集合，也可以将整个商店看作一个集合，这个商店中有人或者其他物品也没有关系。）

②集合里的元素没有顺序

（我们不会这样讲：我想要集合中的第三个元素，因为集合是没有顺序的。）

事实上，这样的集合并不直接存在于编程语言中。然而，实际编程语言中的很多数据结构，就是在集合的基础上添加了一些规则形成的。

②列表

列表（又称线性列表）的定义

是一种数据项构成的有限序列，即按照一定的线性顺序，排列而成的数据项的集合。

列表的概念是在集合的特征上形成的，它具有顺序，且长度是可变的。你可以把它看作一张购物清单：

列表的特性

在这张清单中：

·购物清单中的条目代表的类型可能不同，但是按照一定顺序进行了排列；
·购物清单的长度是可变的，你可以向购物清单中增加、删除条目。
在编程语言中，列表最常见的表现形式有数组和链表，而我们熟悉的栈和队列则是两种特殊类型的列表。除此之外，向列表中添加、删除元素的具体实现方式会根据编程语言的不同而有所区分。

③数组

数组是列表的实现方式之一，也是面试中经常涉及到的数据结构。

数组的特性

正如前面提到的，数组是列表的实现方式，它具有列表的特征，同时也具有自己的一些特征。然而，在具体的编程语言中，数组这个数据结构的实现方式具有一定差别。比如 C++ 和 Java 中，数组中的元素类型必须保持一致，而 Python 中则可以不同。Python 中的数组叫做 list，具有更多的高级功能。

那么如何从宏观上区分列表和数组呢？这里有一个重要的概念：索引。

首先，数组会用一些名为 索引 的数字来标识每项数据在数组中的位置，且在大多数编程语言中，索引是从 0 算起的。我们可以根据数组中的索引，快速访问数组中的元素。

而列表中没有索引，这是数组与列表最大的不同点。

其次，数组中的元素在内存中是连续存储的，且每个元素占用相同大小的内存。要理解这一点，我们需要了解数组在内存中的存储方式，我们将在下一节中详细介绍。

相反，列表中的元素在内存中可能彼此相邻，也可能不相邻。比如列表的另一种实现方式——链表，它的元素在内存中则不一定是连续的。

A 数组的操作

本节我们重点来讲解一下数组的 4 种操作。

①读取元素

读取数组中的元素，是通过访问索引的方式来读取的，索引一般从 0 开始。

在计算机中，内存可以看成一些已经排列好的格子，每个格子对应一个内存地址。一般情况下，数据会分散地存储在不同的格子中。

而对于数组，计算机会在内存中为其申请一段连续的空间，并且会记下索引为 0 处的内存地址。以数组 [“C”, “O”, “D”, “E”, “R”] 为例，它的各元素对应的索引及内存地址如下图所示。

假如我们想要访问索引为 2 处的元素 "D" 时，计算机会进行以下计算：

·找到该数组的索引 0 的内存地址： 2008；
·将内存地址加上索引值，作为目标元素的地址，即 2008 + 2 = 2010，对应的元素为 "D"，这时便找到了目标元素。
我们知道，计算内存地址这个过程是很快的，而我们一旦知道了内存地址就可以立即访问到该元素，因此它的时间复杂度是常数级别，为 O(1)。

②查找元素

假如我们对数组中包含哪些元素并不了解，只是想知道其中是否含有元素 "E"，数组会如何查找元素 "E" 呢？

与读取元素类似，由于我们只保存了索引为0处的内存地址，因此在查找元素时，只需从数组开头逐步向后查找就可以了。如果数组中的某个元素为目标元素，则停止查找；否则继续搜索直到到达数组的末尾。

我们发现，最坏情况下，搜索的元素为 "R"，或者数组中不包含目标元素时，我们需要查找 n 次，n 为数组的长度，因此查找元素的时间复杂度为 O(N)，N为数组的长度N为数组的长度。

③插入元素

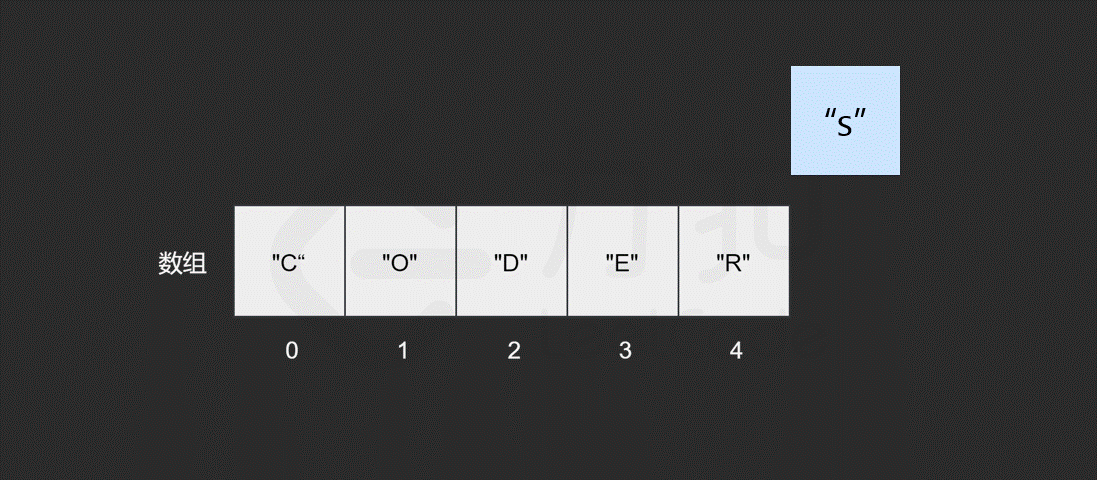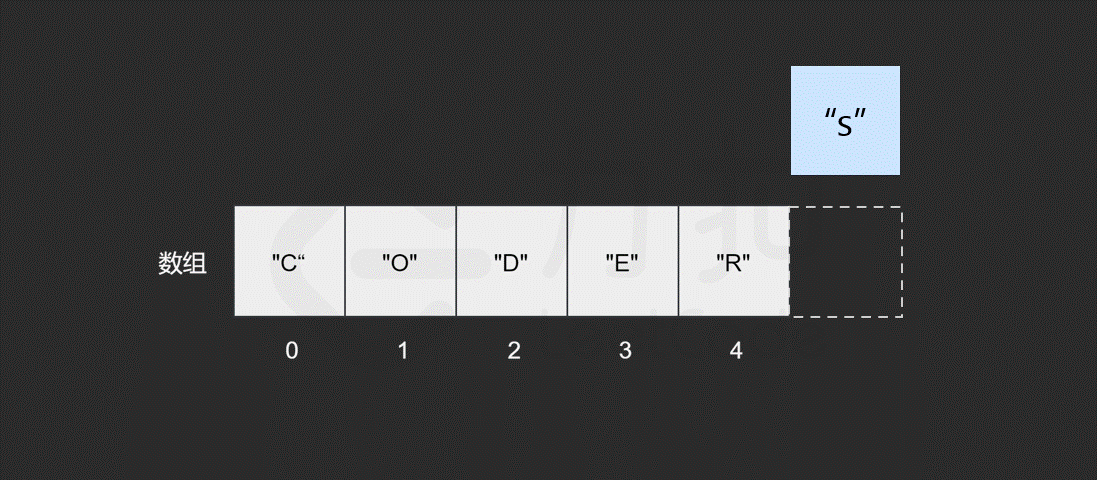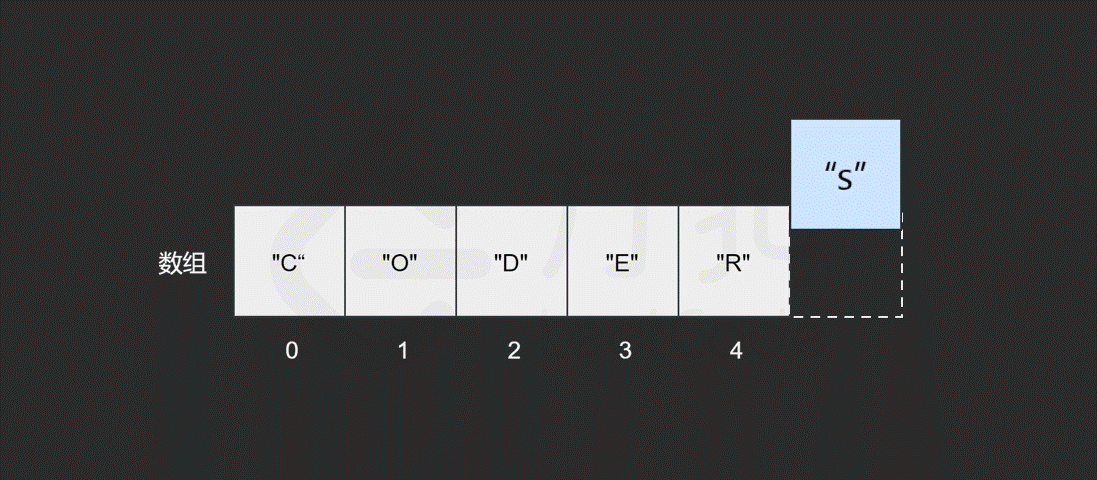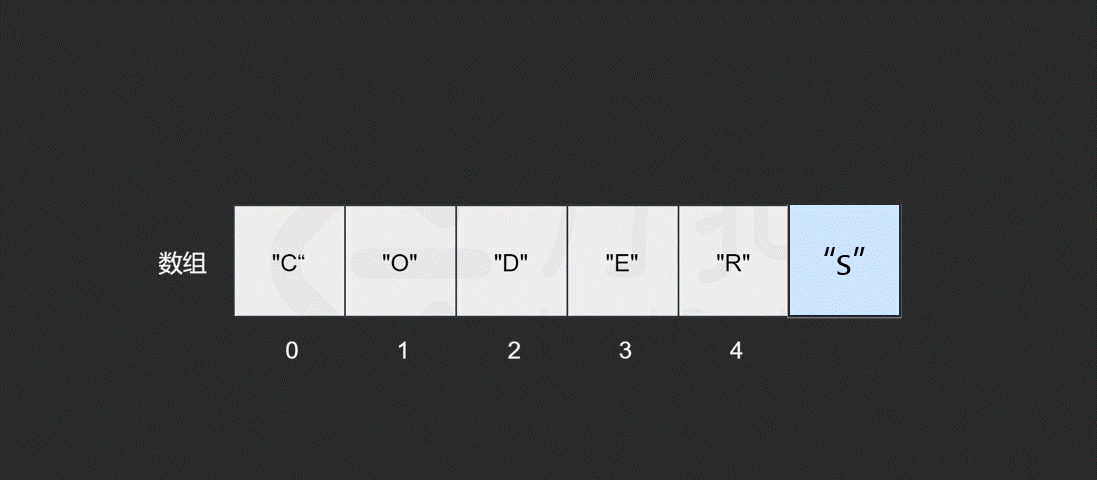
假如我们想在原有的数组中再插入一个元素 "S" 呢？

如果要将该元素插入到数组的末尾，只需要一步。即计算机通过数组的长度和位置计算出即将插入元素的内存地址，然后将该元素插入到指定位置即可。

然而，如果要将该元素插入到数组中的其他位置，则会有所区别，这时我们首先需要为该元素所要插入的位置腾出空间，然后进行插入操作。比如，我们想要在索引 2 处插入 "S"。

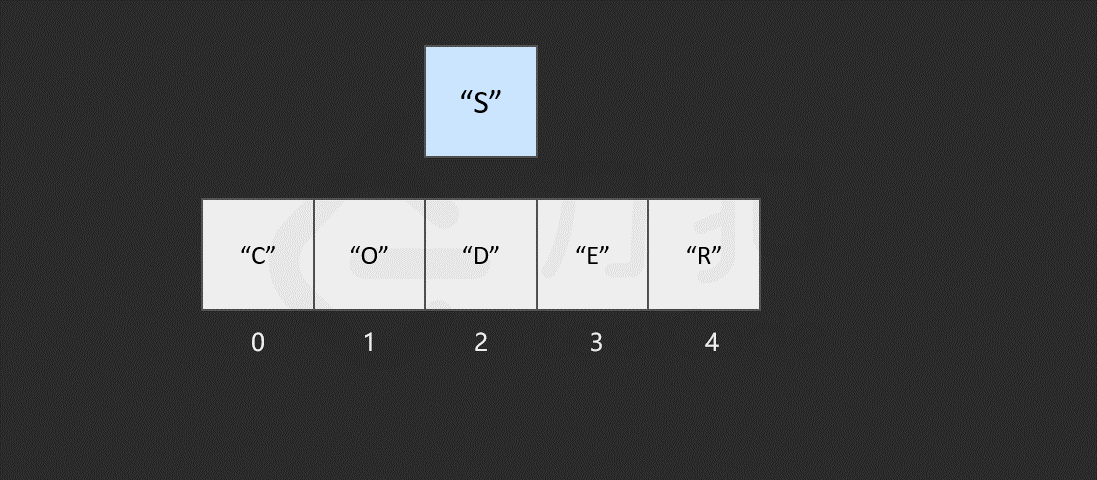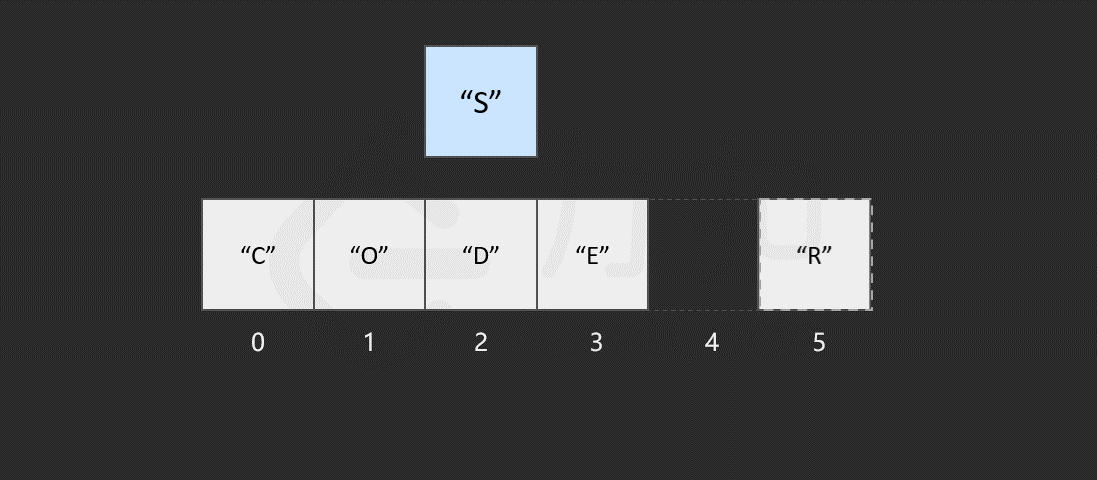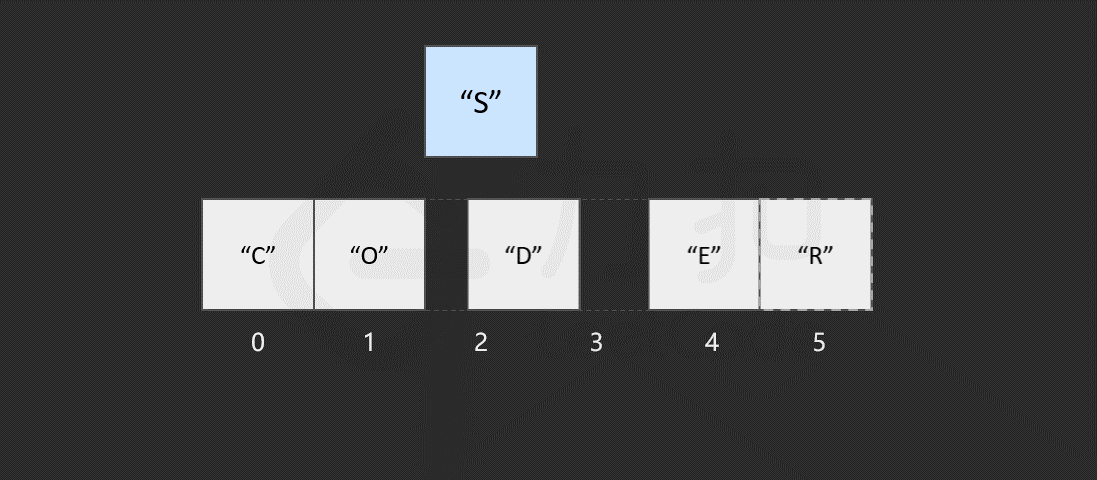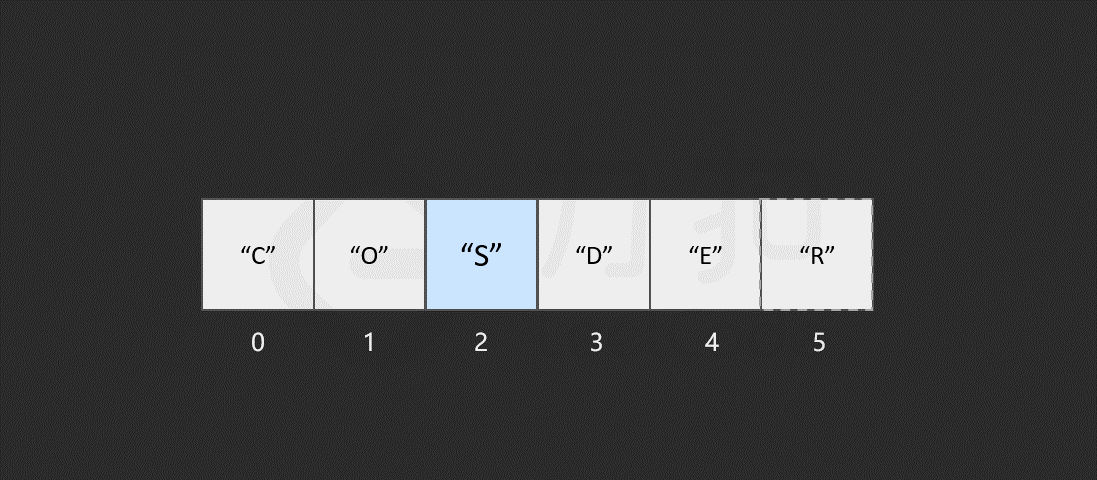
我们发现，如果需要频繁地对数组元素进行插入操作，会造成时间的浪费。事实上，另一种数据结构，即链表可以有效解决这个问题。

④删除元素

删除元素与插入元素的操作类似，当我们删除掉数组中的某个元素后，数组中会留下空缺的位置，而数组中的元素在内存中是连续的，这就使得后面的元素需对该位置进行填补操作。

以删除索引 1 中的元素 "O" 为例，具体过程如图所示。

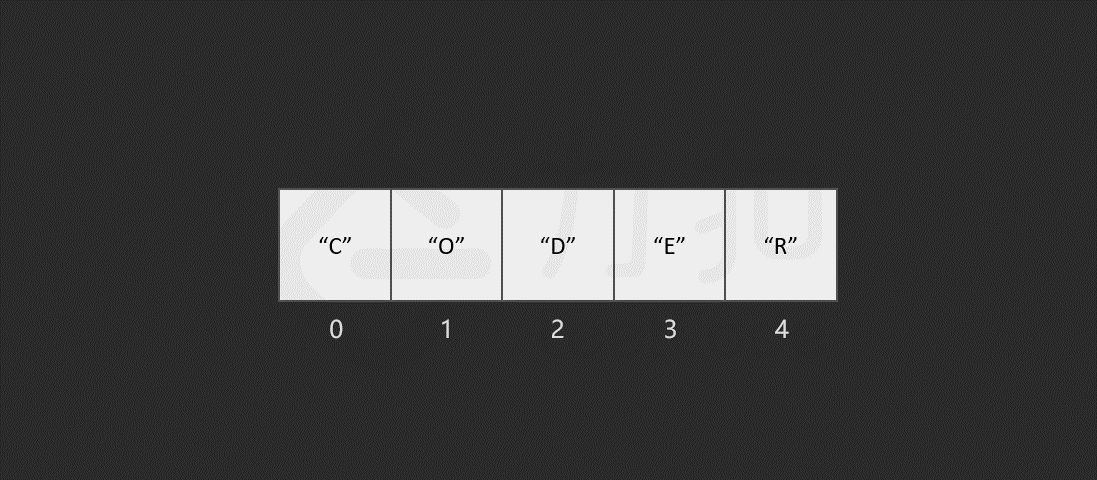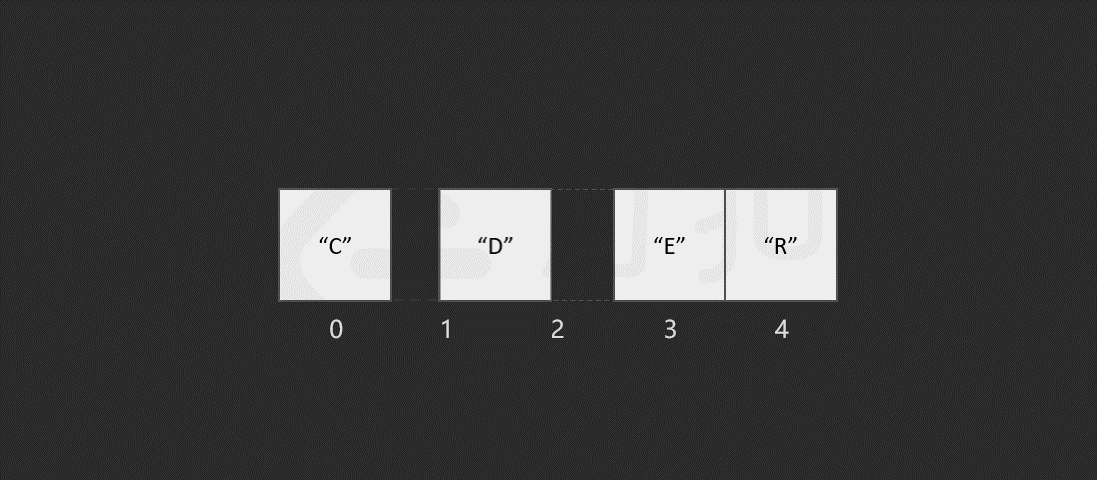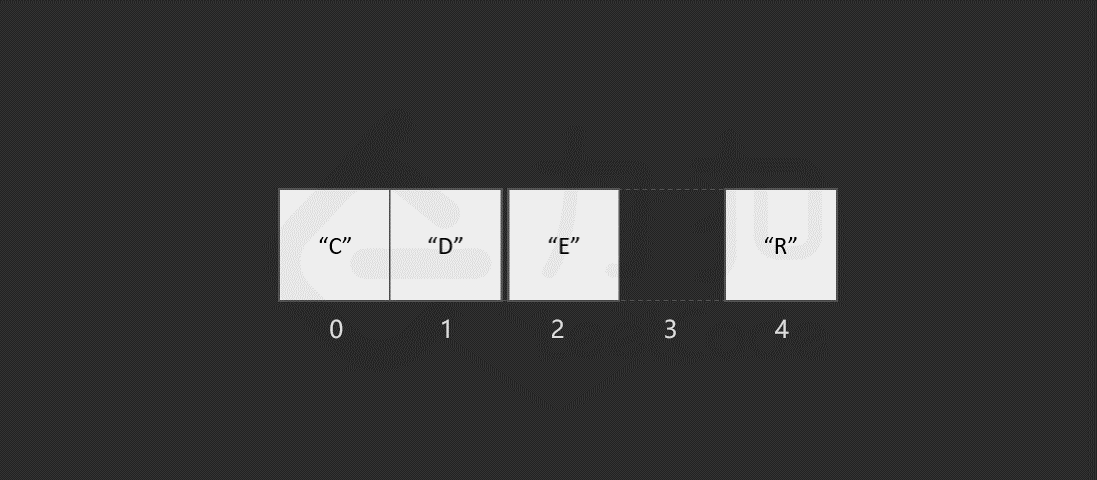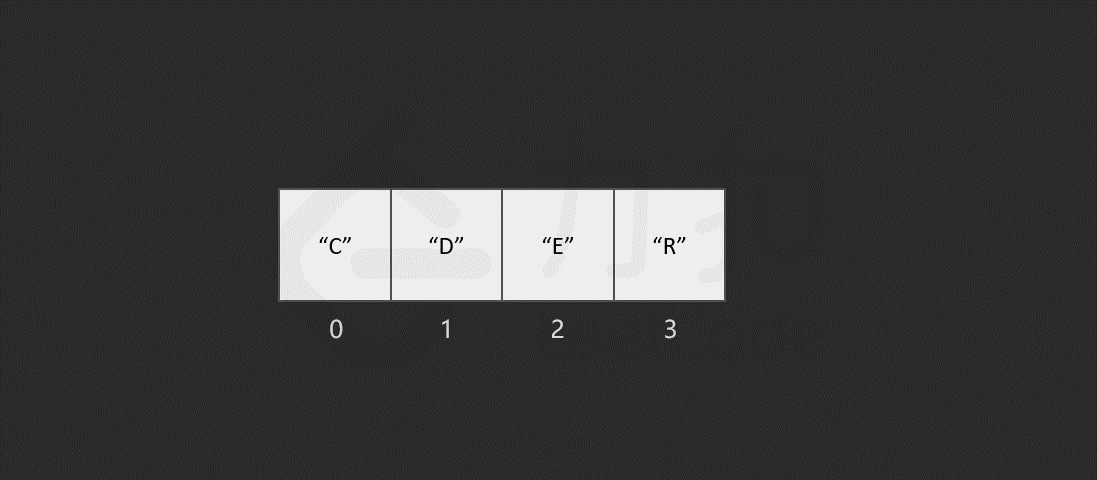
当数组的长度为 n 时，最坏情况下，我们删除第一个元素，共需要的步骤数为 1 + (n - 1) = n 步，其中，1 为删除操作，n - 1 为移动其余元素的步骤数。删除操作具有线性时间复杂度，即时间复杂度为O*(N)，*N 为数组的长度。

2.二维数组简介

A 二维数据简介

二维数组是一种结构较为特殊的数组，只是将数组中的每个元素变成了一维数组。

所以二维数组的本质上仍然是一个一维数组，内部的一维数组仍然从索引 0 开始，我们可以将它看作一个矩阵，并处理矩阵的相关问题。

示例

类似一维数组，对于一个二维数组 A = [[1, 2, 3, 4],[2, 4, 5, 6],[1, 4, 6, 8]]，计算机同样会在内存中申请一段连续的空间，并记录第一行数组的索引位置，即 A[0][0] 的内存地址，它的索引与内存地址的关系如下图所示。

注意，实际数组中的元素由于类型的不同会占用不同的字节数，因此每个方格地址之间的差值可能不为 1。

实际题目中，往往使用二维数组处理矩阵类相关问题，包括矩阵旋转、对角线遍历，以及对子矩阵的操作等。

3.字符串简介

A 字符串简介

维基百科：字符串是由零个或多个字符组成的有限序列。一般记为 s = a1a2…an。它是编程语言中表示文本的数据类型。

1.字符串的基本操作对象通常是字符串整体或者其子串

2. 字符串操作比其他数据类型更复杂（例如比较、连接操作）

①比较函数

字符串有它自己的比较函数（我们将在下面的代码中向你展示比较函数的用法）。

然而，存在这样一个问题：

我们可以用 “==” 来比较两个字符串吗？

这取决于下面这个问题的答案：

我们使用的语言是否支持运算符重载？

如果答案是 yes （例如 C++、Python）。我们可以使用 == 来比较两个字符串；
如果答案是 no （例如 Java），我们可能无法使用 == 来比较两个字符串。当我们使用 == 时，它实际上会比较这两个对象是否是同一个对象。

②连接操作

对于不同的编程语言中，字符串可能是可变的，也可能是不可变的。不可变意味着一旦字符串被初始化，你就无法改变它的内容。

在某些语言（如 C ++）中，字符串是可变的，可以像在数组中那样修改字符串。
在其他一些语言（如 Java、Python）中，字符串是不可变的。

在 字符串不可变 的语言中，进行字符串的连接操作则会带来一些问题。

对于 Java来说，由于字符串是不可变的，因此在连接时首先为新字符串分配足够的空间，复制旧字符串中的内容并附加到新字符串。

因此，总时间复杂度将是：

5+5×2+5×3+…+5×n=5×(1+2+3+…+n)=5×n×(n+1)/2 即 O*(N2)。

针对 Java 中出现的此问题，我们提供了以下解决方案：

如果你确实希望你的字符串是可变的，则可以使用 toCharArray 将其转换为字符数组。
如果你经常必须连接字符串，最好使用一些其他的数据结构，如 StringBuilder 。

A （选修）字符串匹配算法：KMP

Knuth–Morris–Pratt（KMP）算法是一种改进的字符串匹配算法，它的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。它的时间复杂度是 O*(m+*n)。

情景1

假如你是一名生物学家，现在，你的面前有两段 DNA 序列 S 和 T，你需要判断 T 是否可以匹配成为 S 的子串。

你可能会凭肉眼立即得出结论：是匹配的。可是计算机没有眼睛，只能对每个字符进行逐一比较。

对于计算机来讲，首先它会从左边第一个位置开始进行逐一比较：

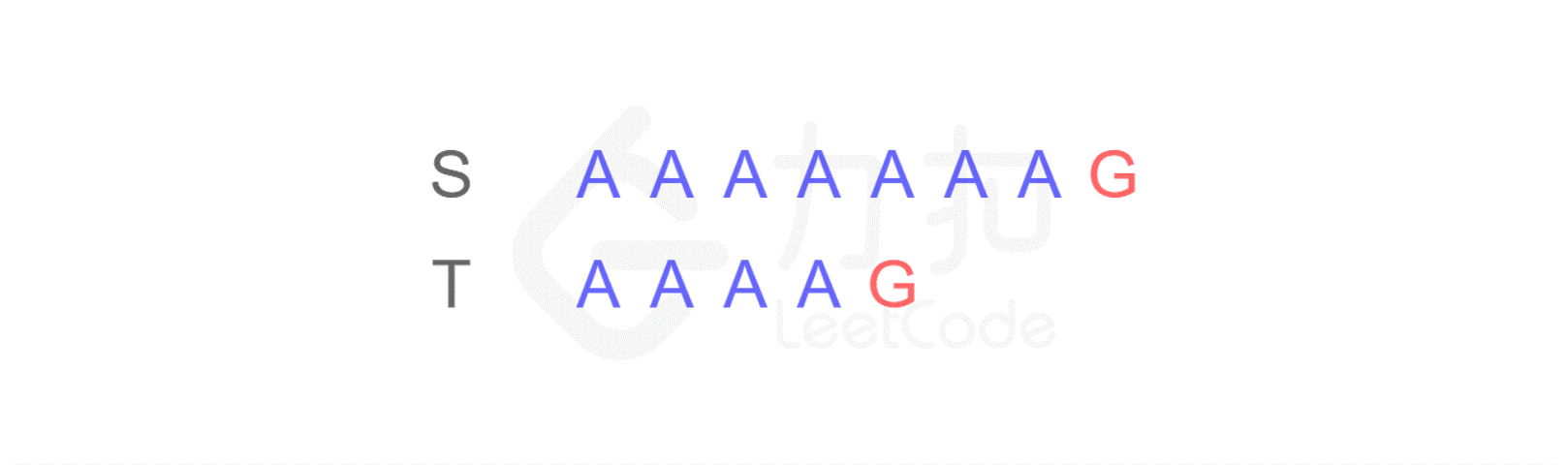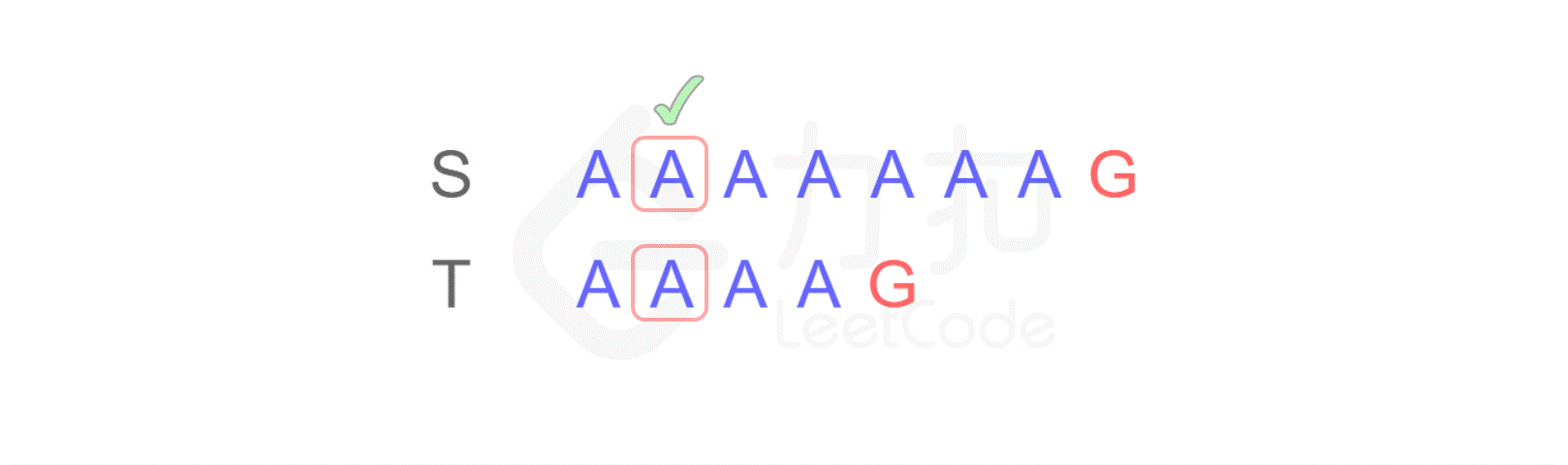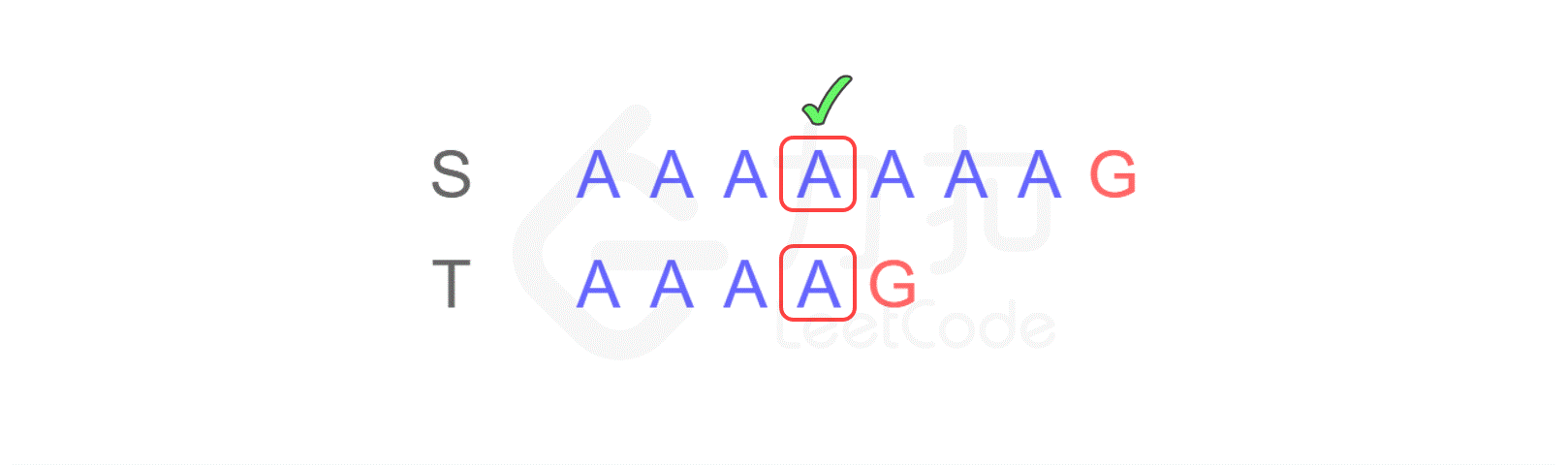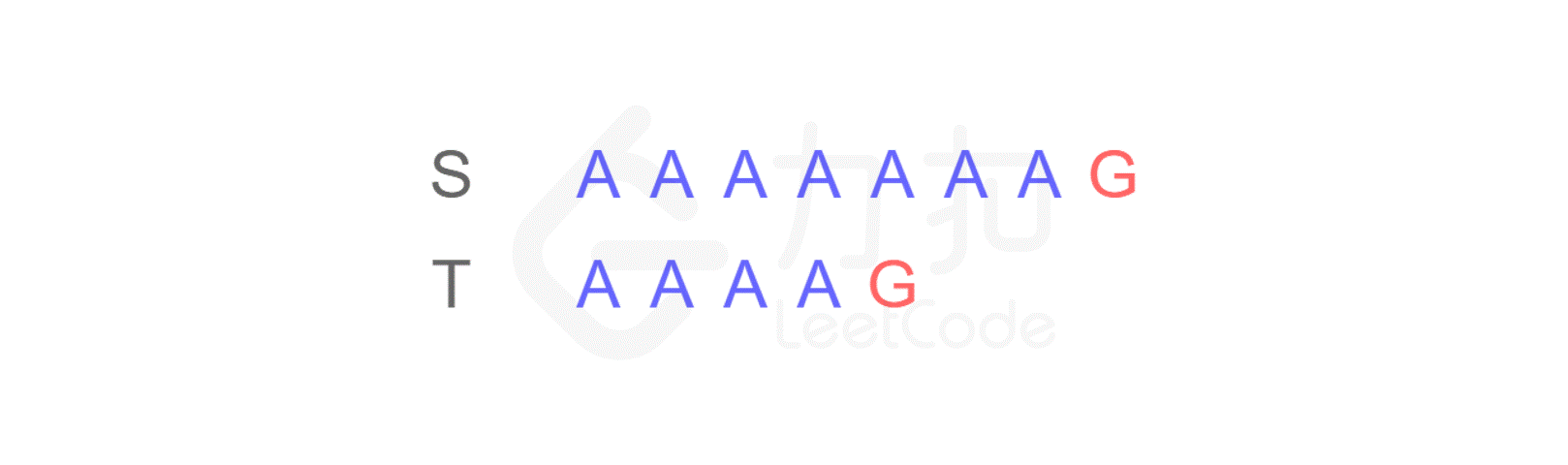
这样，当匹配到 T 的最后一个字符时，发现不匹配，于是从 S 的第二个字符开始重新进行比较：

仍然不匹配，再次将 T 与 S 的第三个字符开始匹配…不断重复以上步骤，直到从 S 的第四个字符开始时，最终得出结论：S 与 T 是匹配的。

你发现这个方法的弊端了吗？我们在进行每一轮匹配时，总是会重复对 A 进行比较。也就是说，对于 S 中的每个字符，我们都需要从 T 第一个位置重新开始比较，并且 S 前面的 A 越多，浪费的时间也就越多。假设 S 的长度为 m，T 的长度为 n，理论上讲，最坏情况下迭代 m−n+1 轮，每轮最多进行 n 次比对，一共比较了(m−n+1)×n 次，当 m*>>n时，渐进时间复杂度为 O(*mn)。

而 KMP 算法的好处在于，它可以将时间复杂度降低到 O*(m+*n)，字符序列越长，该算法的优势越明显。

情景2

再来举一个例子，现在有如下字符串 S 和 P，判断 P 是否为 S 的子串。

我们仍然按照原来的方式进行比较，比较到 P 的末尾时，我们发现了不匹配的字符。

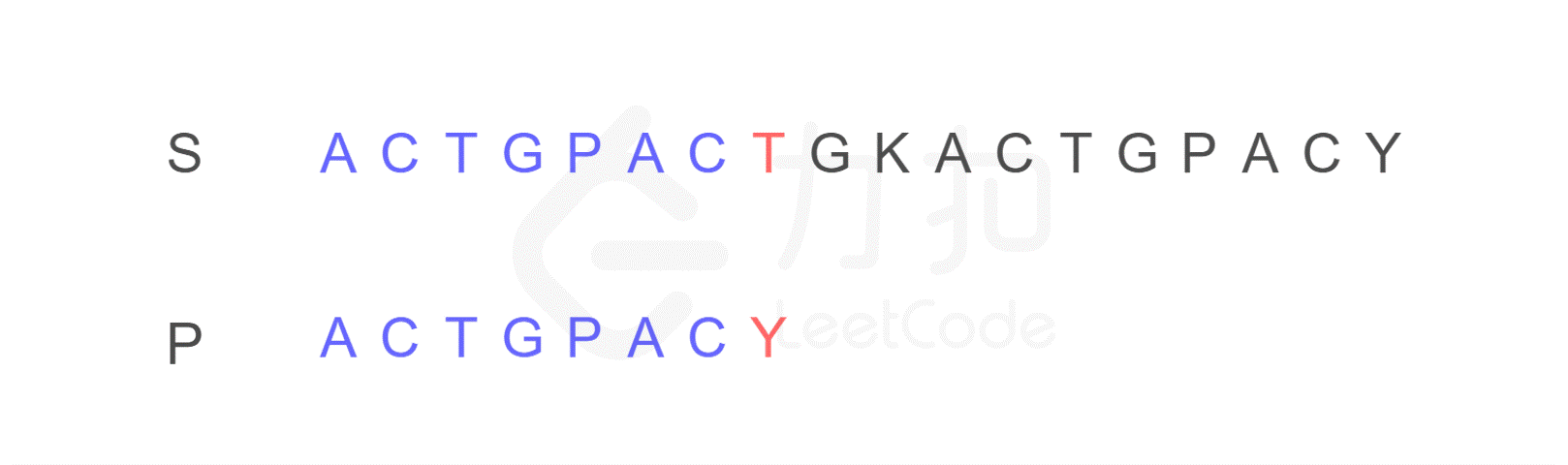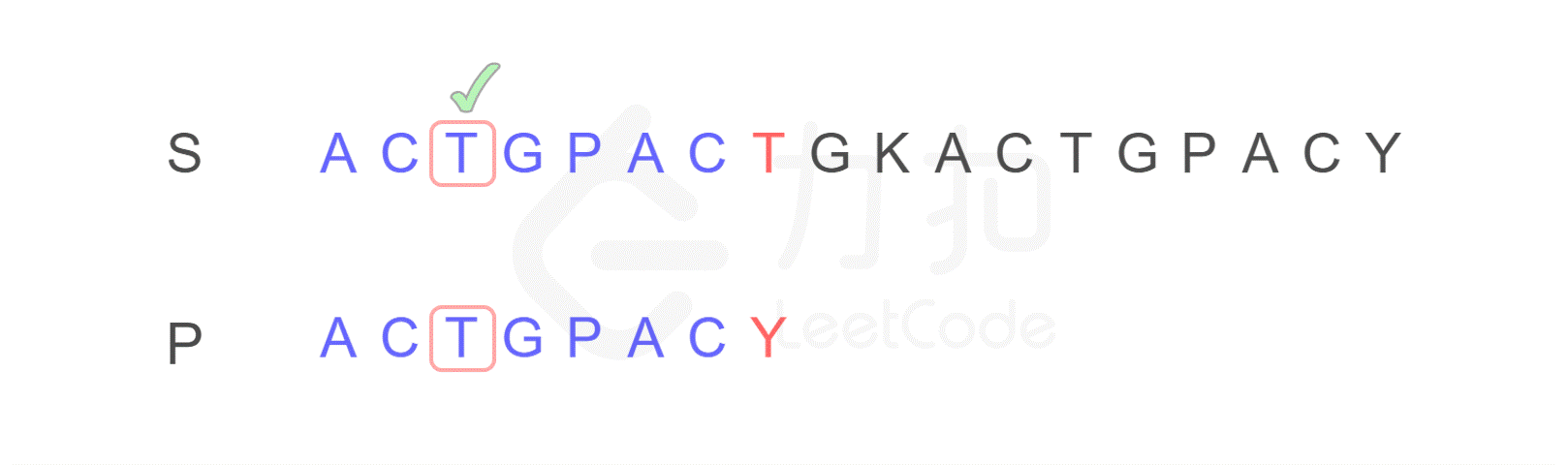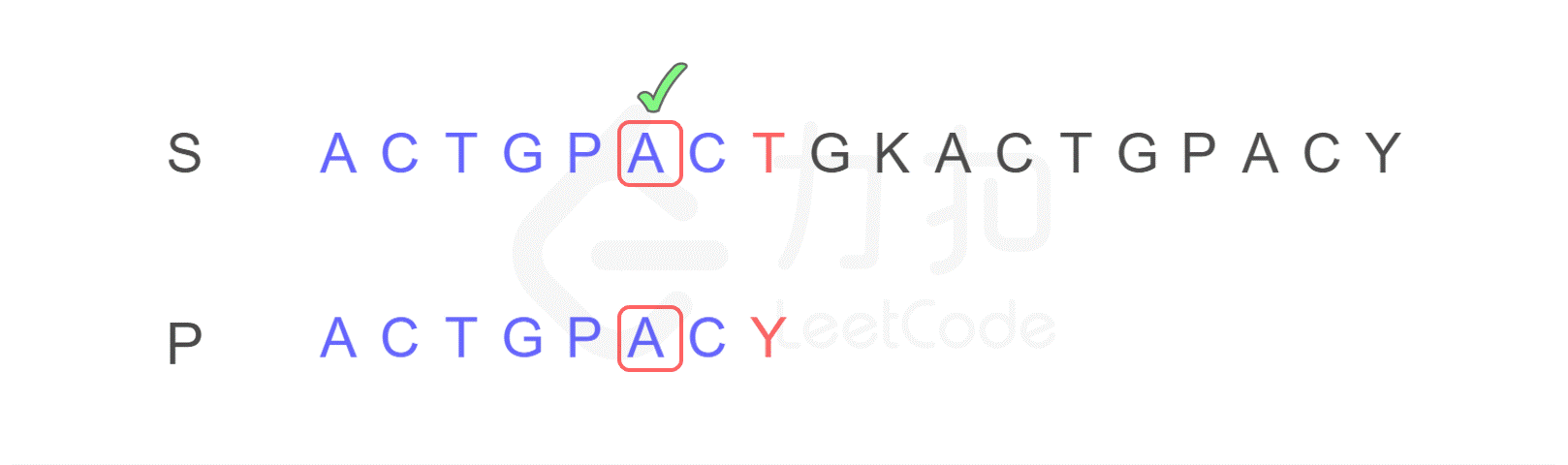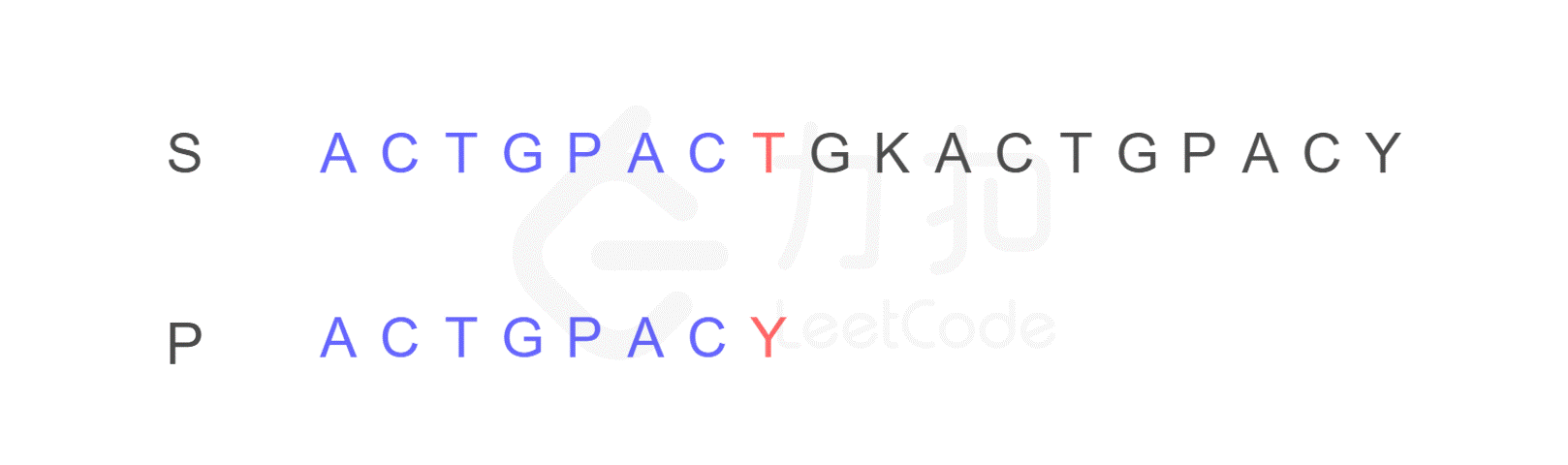
注意，按照原来的思路，我们下一步应将字符串 P 的开头，与字符串 S 的第二位 C 重新进行比较。而 KMP 算法告诉我们，我们只需将字符串 P 需要比较的位置重置到图中 j 的位置，S 保持 i 的位置不变，接下来即可从 i，j 位置继续进行比较。

为什么？我们发现字符串 P 有子串 ACT 和 ACY，当 T 和 Y 不匹配时，我们就确定了 S 中的蓝色 AC 并不匹配 P 右侧的 AC，但是可能匹配左侧的 AC，所以我们从位置 i 和 j 继续比较。

换句话说，Y 对应下标 2，表示下一步要重新开始的地方。

既然如此，如果每次不匹配的时候，我们都能立刻知道 P 中不匹配的元素，下一步应该从哪个下标重新开始，这样不就能大大简化匹配过程了吗？这就是 KMP 的核心思想。

KMP 算法中，使用一个数组 next 来保存 P 中元素不匹配时，下一步应该重新开始的下标。由于计算机不能像我们人类一样，通过视觉来得出结论，因此这里有一种适合计算机的构造 next 数组的方法。

小插曲：构造 next 数组

构造方法为：**next[i] 对应的下标，为 P[0...i - 1] 的最长公共前缀后缀的长度，令 next[0] = -1。**具体解释如下：

例如对于字符串 abcba：

前缀：它的前缀包括：a, ab, abc, abcb，不包括本身；
后缀：它的后缀包括：bcba, cba, ba, a，不包括本身；
最长公共前缀后缀：abcba 的前缀和后缀中只有 a 是公共部分，字符串 a 的长度为 1。

所以，我们将 P[0...i - 1] 的最长公共前后缀的长度作为 next[i] 的下标，就得到了 next 数组。

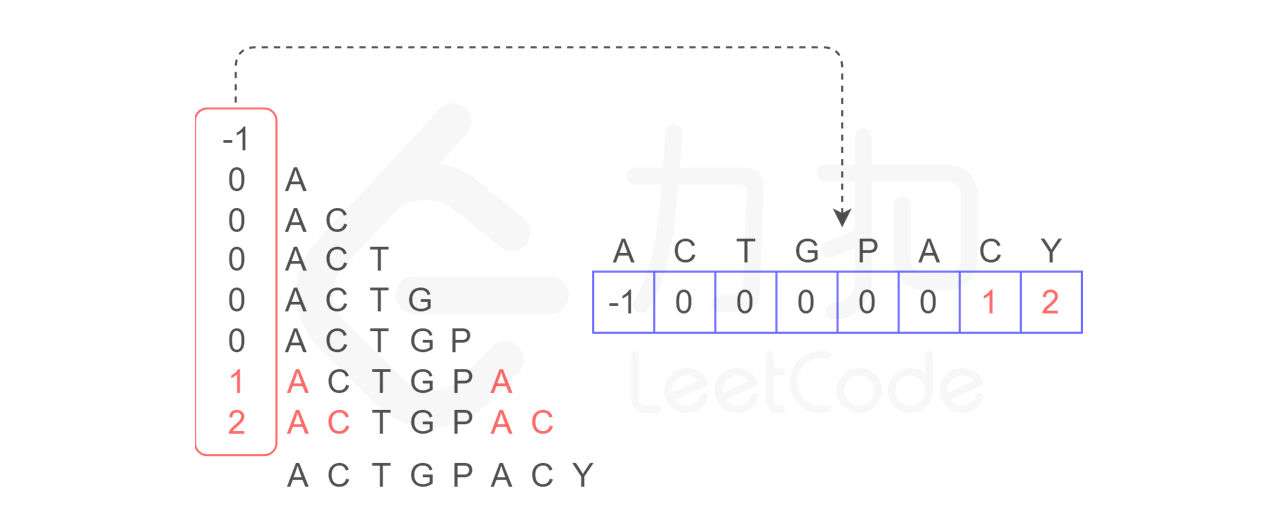
回到情景2

上次我们还停留在位置 i 和 j，现在继续进行比较。从如下图所示，由于我们已经构造了 next 数组，当继续移动到图中的 r 和 c 位置时，发现不匹配，根据 next 数组，我们可以立即将位置 c 回到下标 0 的位置：

之后的情形就很简单了：

K 与 A 不匹配，查看 next 数组，A 对应 next 中的元素为 -1，表示不动，r 加 1；
位置 r 字符与位置 c 字符匹配，继续比较下一位；
后面元素均匹配，最终找到匹配元素。

结尾

最后，我们给出相关代码。

KMP 主算法参考代码（保证存在有效解）：

public class KMP {
    // KMP 算法匹配字符串
    public static int match(char[] P, char[] S) {
        int[] next = buildNext(P); // 构造 next 表
        int m = S.length, i = 0; // 文本串指针
        int n = P.length, j = 0; // 模式串指针

        // 自左向右逐个比对字符
        while (j < n && i < m) {
            if (j < 0 || S[i] == P[j]) { // 若匹配，或 P 已移除最左侧
                i++; // 文本串指针向后移动
                j++; // 模式串指针向后移动
            } else {
                j = next[j]; // 模式串右移（注意：文本串不用回退）
            }
        }

        return i - j; // 返回匹配的起始位置
    }

    // 构造模式串 P 的 next 表
    private static int[] buildNext(char[] P) {
        int m = P.length;
        int[] next = new int[m];
        int t = next[0] = -1; // 初始化 t 为 -1，表示当前没有前缀与后缀匹配
        int j = 0; // 模式串指针

        // 逐步计算 next 表的每一项
        while (j < m - 1) {
            if (0 > t || P[j] == P[t]) { // 匹配成功或者已经没有前缀可以匹配
                j++; // 模式串指针向后移动
                t++; // 更新 next 表的值为当前匹配长度
                next[j] = (P[j] != P[t]) ? t : next[t]; // 更新 next 表的值
            } else {
                t = next[t]; // 回溯到前缀的后缀进行匹配
            }
        }

        return next; // 返回构造好的 next 表
    }

    public static void main(String[] args) {
        char[] pattern = "ababcababcabcabc".toCharArray();
        char[] text = "ababcabcabcabcabcababcabcabcabc".toCharArray();

        int result = match(pattern, text);
        System.out.println("Pattern found at index: " + result);
    }
}

4.双指针技巧

A 双指针技巧——情景一

在上一章中，我们通过迭代数组来解决一些问题。通常，我们只需要一个指针进行迭代，即从数组中的第一个元素开始，最后一个元素结束。然而，有时我们会使用两个指针进行迭代。

示例

让我们从一个经典问题开始：

反转数组中的元素。比如数组为 ['l', 'e', 'e', 't', 'c', 'o', 'd', 'e']，反转之后变为 ['e', 'd', 'o', 'c', 't', 'e', 'e', 'l']。

使用双指针技巧，其思想是分别将两个指针分别指向数组的开头及末尾，然后将其指向的元素进行交换，再将指针向中间移动一步，继续交换，直到这两个指针相遇。

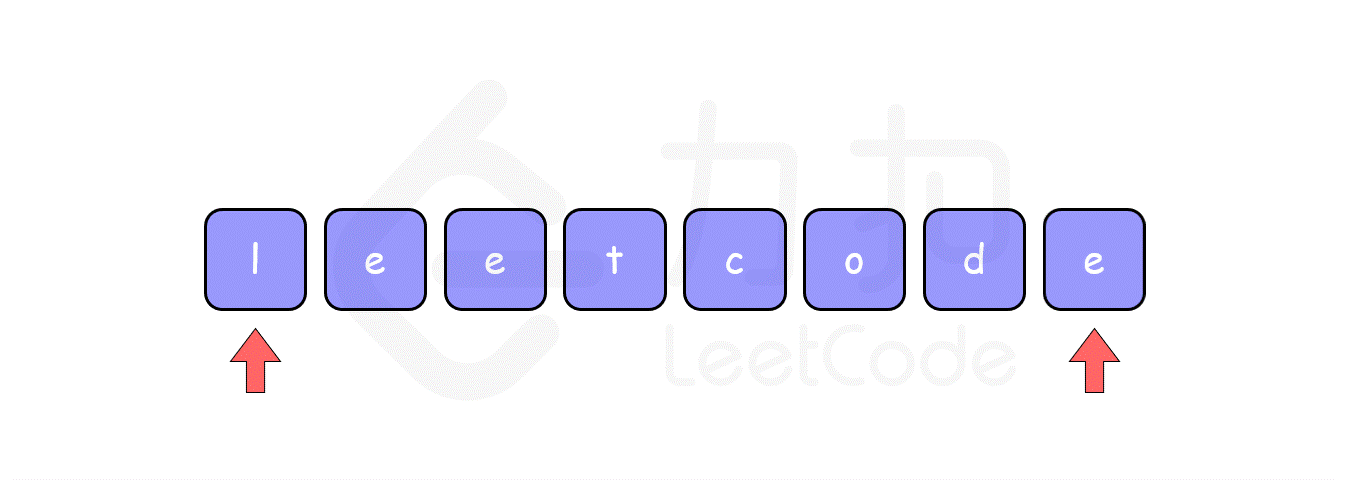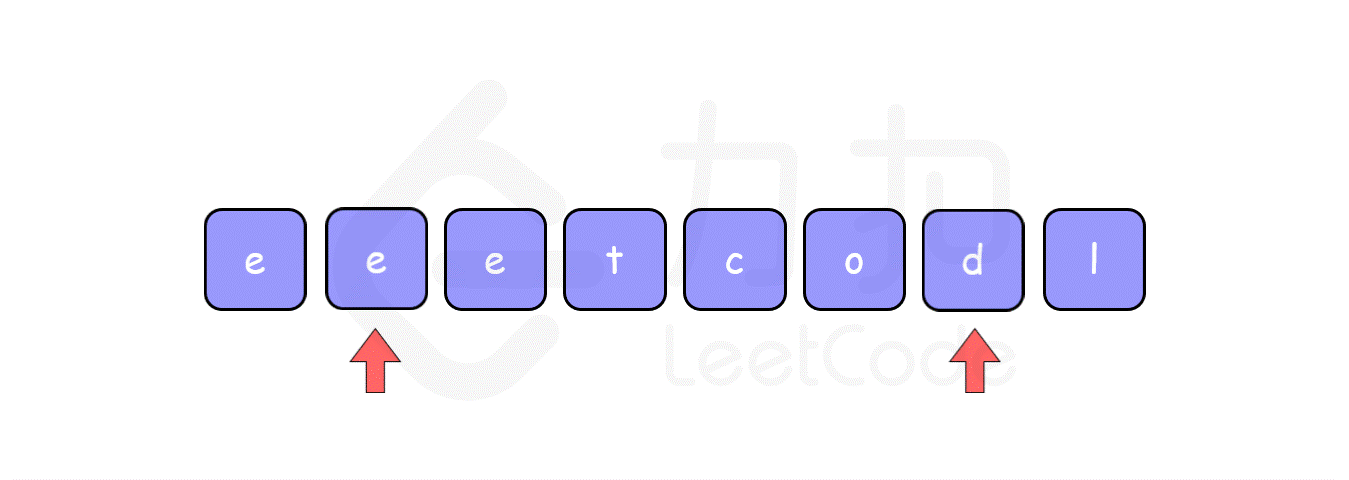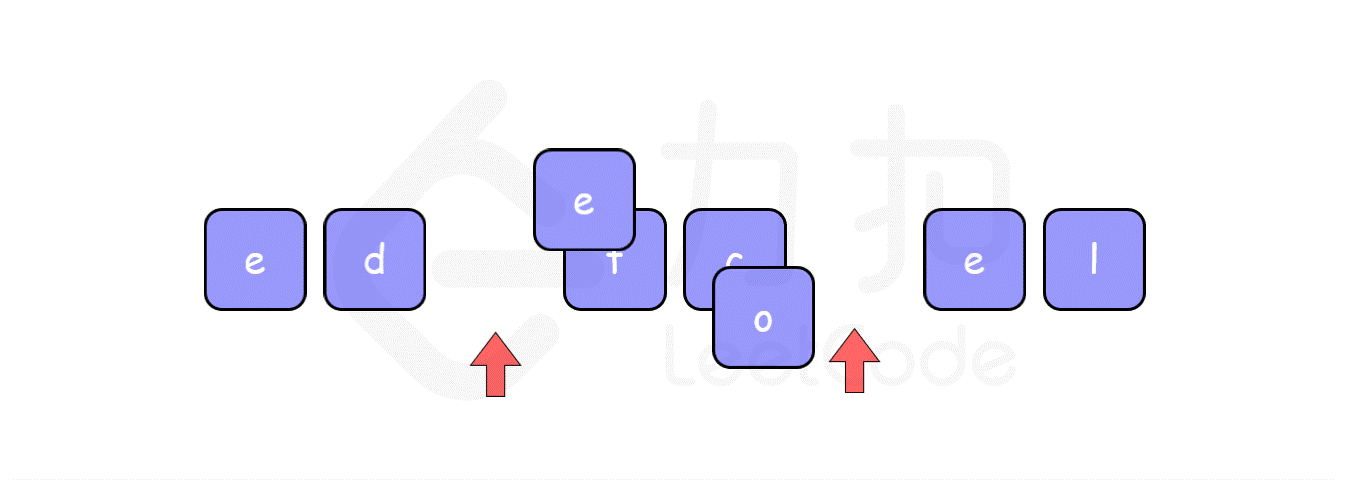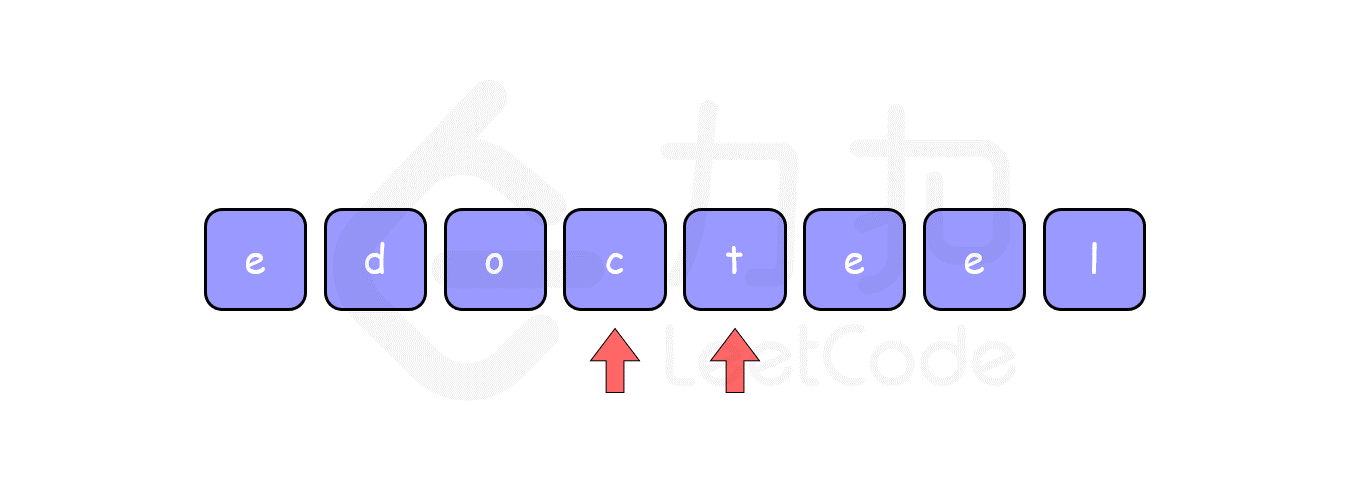
代码参考

public void reverseString(char[] s) {
        int i = 0;
        int j = s.length - 1;
        while (i < j) {
            // 交换字符
            char temp = s[i];
            s[i] = s[j];
            s[j] = temp;
            
            // 移动指针
            i++;
            j--;
        }

小结

我们来总结一下，使用双指针的典型场景之一是你想要

从两端向中间迭代数组。

这时你可以使用双指针技巧：

一个指针从头部开始，而另一个指针从尾部开始。

这种技巧经常在排序数组中使用。

A 双指针技巧——情景二

有时，我们可以使用两个不同步的指针来解决问题，即快慢指针。与情景一不同的是，两个指针的运动方向是相同的，而非相反。

示例

让我们从一个经典问题开始：

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

如果我们没有空间复杂度上的限制，那就更容易了。我们可以初始化一个新的数组来存储答案。如果元素不等于给定的目标值，则迭代原始数组并将元素添加到新的数组中。

实际上，它相当于使用了两个指针，一个用于原始数组的迭代，另一个总是指向新数组的最后一个位置。

考虑空间限制

如果我们不使用额外的数组，只是在原数组上进行操作呢？

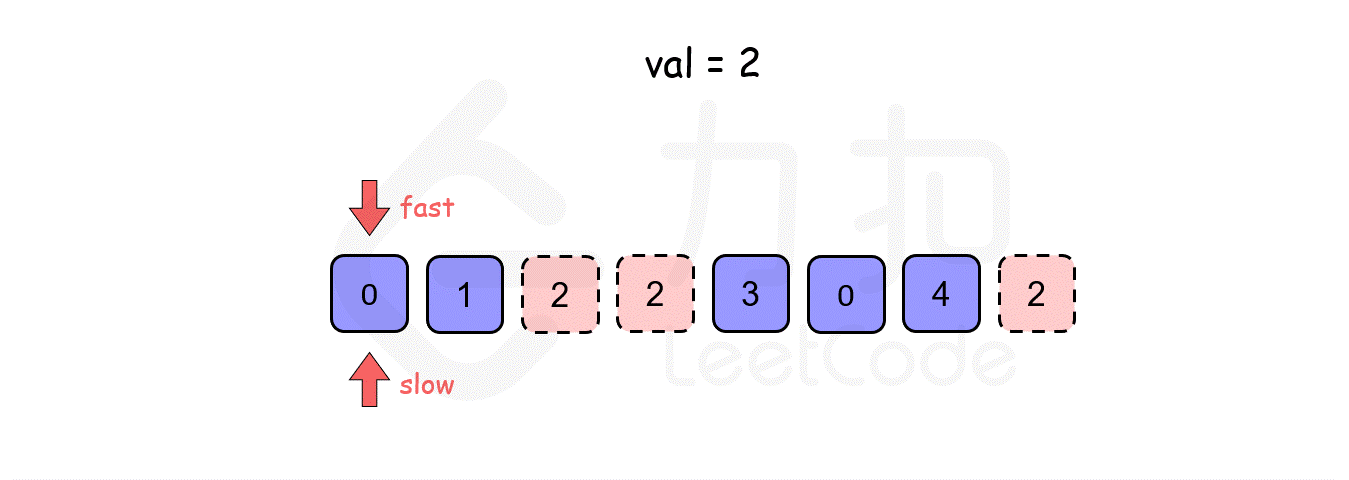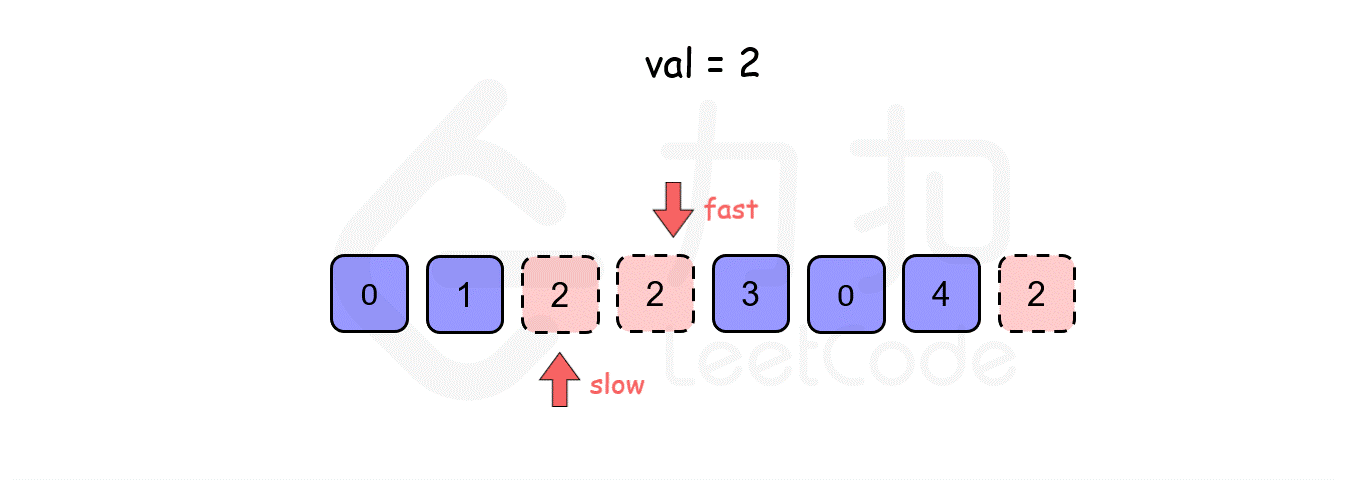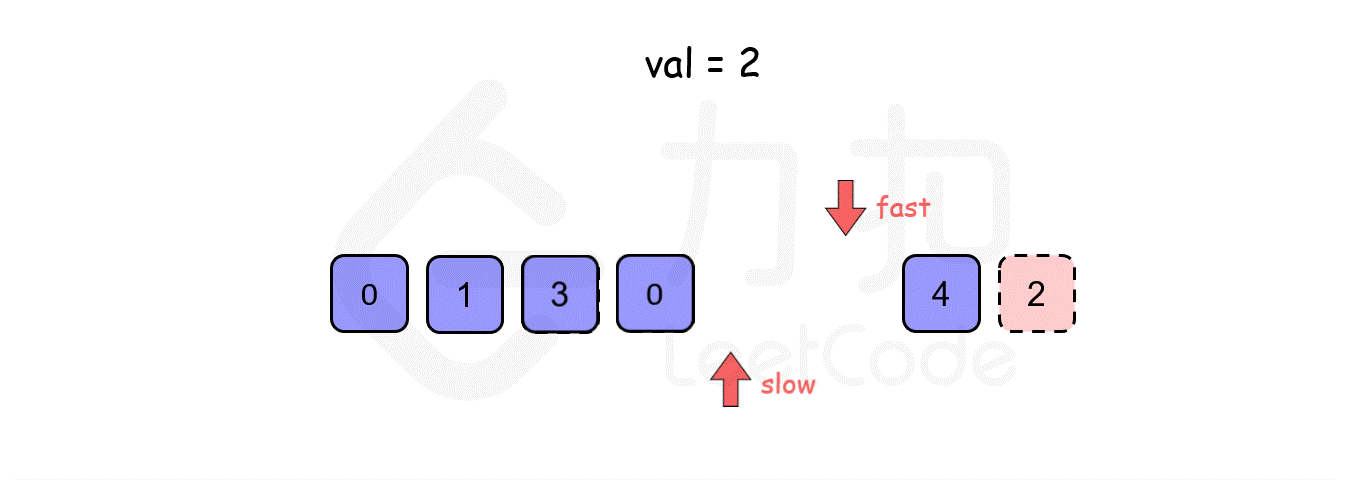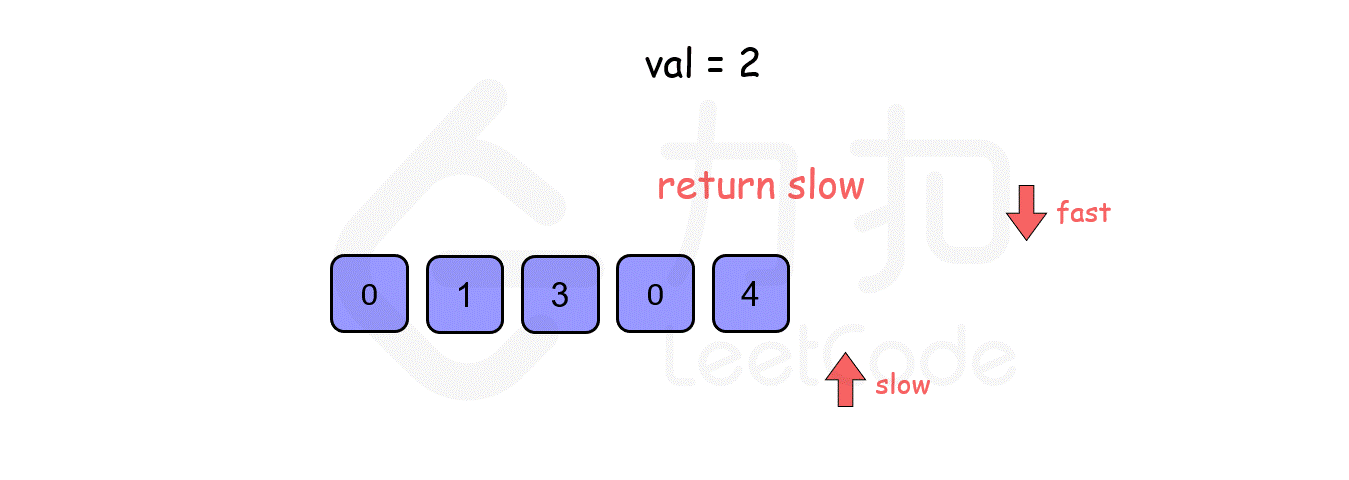
此时，我们就可以采用快慢指针的思想：初始化一个快指针 fast 和一个慢指针 slow，fast 每次移动一步，而 slow 只当 fast 指向的值不等于 val 时才移动一步。

代码参考

public int removeElement(int[] nums, int val) {
        int slow = 0;
        int n = nums.length;
        
        for (int fast = 0; fast < n; fast++) {
            if (nums[fast] != val) {
                nums[slow] = nums[fast];
                slow++;
            }
        }
        
        return slow;
    }