2807. 在链表中插入最大公约数 辗转相除和BigDecimal自带求公约数实现

2807. 在链表中插入最大公约数

给你一个链表的头 head ，每个结点包含一个整数值。

在相邻结点之间，请你插入一个新的结点，结点值为这两个相邻结点值的 最大公约数 。

请你返回插入之后的链表。

两个数的 最大公约数 是可以被两个数字整除的最大正整数。

示例 1：

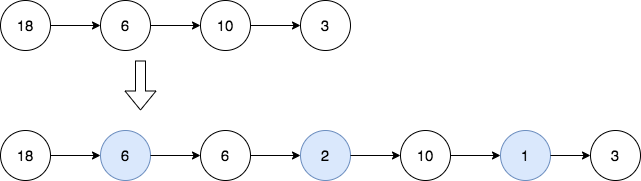
输入：head = [18,6,10,3]
输出：[18,6,6,2,10,1,3]
解释：第一幅图是一开始的链表，第二幅图是插入新结点后的图（蓝色结点为新插入结点）。
- 18 和 6 的最大公约数为 6 ，插入第一和第二个结点之间。
- 6 和 10 的最大公约数为 2 ，插入第二和第三个结点之间。
- 10 和 3 的最大公约数为 1 ，插入第三和第四个结点之间。
所有相邻结点之间都插入完毕，返回链表。

提示：

• 链表中结点数目在 [1, 5000] 之间。
• 1 <= Node.val <= 1000

实现过程

25min

只需要注意插入链表的方法就好。

递归的方法：

1.确认递归变量

2.确认终止条件

3.写每一层的递归

   public ListNode insertGreatestCommonDivisors(ListNode head) {
// 如果链表为空或只有一个节点，直接返回
    if (head == null || head.next == null) {
        return head;
    }
    
    // 定义指针
    ListNode current = head;

    while (current != null && current.next != null) {
        // 计算相邻节点的最大公约数
        int gcdValue = gcd(current.val, current.next.val);
        
        // 创建新节点来存储最大公约数
        ListNode newNode = new ListNode(gcdValue);
        
        // 插入新节点
        newNode.next = current.next;  // 新节点指向当前节点的下一个节点
        current.next = newNode;       // 当前节点指向新节点
        
        // 移动指针到下一个节点（跳过新插入的节点）
        current = newNode.next;
    }
    return head;
    }
    // public int divisor(int NumberA,int NumberB){
    //     BigInteger x = new BigInteger(NumberA)//可以接收int类型
	//     BigInteger y = BigInteger.valueOf(NumberB);
	//     BigInteger gcd = x.gcd(y);	//BigInteger自带的求最大公约数的方法
    //     return Integer.valueOf(gcd);
    // }
    //辗转相除法 递归法
    public int gcd(int NumberA,int NumberB){
        if(NumberB==0)
            return NumberA;
        else
            return gcd(NumberB,NumberA%NumberB);
         
	}