前言
在本文中,我们将探讨三道有趣的算法题,分别是《地牢大师》、《全球变暖》和《大臣的旅费》。每道题目都有独特的挑战,考验我们在图论、动态规划以及数据结构的运用。通过这些问题,我们不仅能提升算法能力,还能进一步理解如何将理论知识应用到实际问题中,解决复杂的编程任务。
地牢大师
你现在被困在一个三维地牢中,需要找到最快脱离的出路!
地牢由若干个单位立方体组成,其中部分不含岩石障碍可以直接通过,部分包含岩石障碍无法通过。
向北,向南,向东,向西,向上或向下移动一个单元距离均需要一分钟。
你不能沿对角线移动,迷宫边界都是坚硬的岩石,你不能走出边界范围。
请问,你有可能逃脱吗?
如果可以,需要多长时间?
输入格式
输入包含多组测试数据。
每组数据第一行包含三个整数 L,R,C分别表示地牢层数,以及每一层地牢的行数和列数。
接下来是 L 个 R 行 C 列的字符矩阵,用来表示每一层地牢的具体状况。
每个字符用来描述一个地牢单元的具体状况。
其中, 充满岩石障碍的单元格用”#”表示,不含障碍的空单元格用”.”表示,你的起始位置用”S”表示,终点用”E”表示。
每一个字符矩阵后面都会包含一个空行。
当输入一行为”0 0 0”时,表示输入终止。
输出格式
每组数据输出一个结果,每个结果占一行。
如果能够逃脱地牢,则输出”Escaped in x minute(s).”,其中X为逃脱所需最短时间。
如果不能逃脱地牢,则输出”Trapped!”。
数据范围
1≤L,R,C≤100
输入样例:
3 4 5
S....
.###.
.##..
###.#
#####
#####
##.##
##...
#####
#####
#.###
####E
1 3 3
S##
#E#
###
0 0 0
输出样例:
Escaped in 11 minute(s).
Trapped!
算法思路
输入和初始化:
- 读取输入的迷宫的尺寸(l, row, col),其中l是迷宫的层数,row是行数,col是列数。
- 构建一个三维字符数组map来存储迷宫的状态,每个位置可以是墙(‘#’),空地(‘.’),起点(‘S’)或终点(‘E’)。初始化一个三维数组steps,用于记录每个位置的最短步数,初始值设为-1,表示不可达。
BFS算法:
- 使用一个队列q来存储当前需要处理的节点(每个节点是一个三维坐标)。
- 从起点S开始,设定其步数为0,开始进行广度优先搜索。
每次从队列中取出一个节点,检查它的6个可能的相邻位置(上下前后左右六个方向)。 - 对于每个相邻位置,检查是否越界、是否已被访问过、是否是墙(#)。如果合法,更新该位置的步数,并将其加入队列。
- 如果到达终点E,返回当前步数。
- 如果队列为空且未找到终点,说明无法到达终点,返回-1。
输出结果:
- 如果从起点到终点有路径,则输出“Escaped in x minute(s)”,其中x是最短路径的步数。如果无法到达终点,则输出“Trapped!”。
终止条件:
- 当输入的l, row, col均为0时,结束程序。
思路与《从入门到精通:蓝桥杯编程大赛知识点全攻略》(十二)-航班时间、日志统计、献给阿尔吉侬的花束的献给阿尔吉侬的花束基本一致,只不过是换成3维空间。
代码如下
import java.io.*;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 210;
static char[][][] map = new char[N][N][N];
static int[][][] steps = new int[N][N][N];
static int l,row,col;
public static void main(String[] args)throws Exception {
while (true){
String[] s = nextLine().split(" ");
l = Integer.parseInt(s[0]);
row = Integer.parseInt(s[1]);
col = Integer.parseInt(s[2]);
if(l == 0 && row == 0 && col == 0){
break;
}
for(int i = 0;i < l;i++){
for(int j = 0;j < row;j++){
Arrays.fill(steps[i][j], -1);
}
}
Pair start = null;
Pair end = null;
for(int i = 0 ; i < l ; i++){
for(int j = 0 ; j < row ; j++){
map[i][j] = nextLine().toCharArray();
for(int k = 0 ; k < col ; k++){
if(map[i][j][k] == 'S'){
start = new Pair(i,j,k);
steps[i][j][k] = 0;
} else if (map[i][j][k] == 'E') {
end = new Pair(i,j,k);
}
}
}
nextLine();
}
int distance = bfs(start,end);
if(distance == -1){
pw.println("Trapped!");
}else {
pw.println("Escaped in "+distance+" minute(s).");
}
}
pw.flush();
}
public static int bfs(Pair start, Pair end){
int[] dx = {-1,1,0,0,0,0};
int[] dy = {0,0,-1,1,0,0};
int[] dz = {0,0,0,0,-1,1};
Queue<Pair> q = new LinkedList<>();
q.add(start);
while(!q.isEmpty()){
Pair p = q.poll();
for(int i = 0 ; i < 6 ; i++){
int x = p.x + dx[i];
int y = p.y + dy[i];
int z = p.z + dz[i];
if(x < 0 || x >= l || y < 0 || y >= row || z < 0 || z >= col || steps[x][y][z] != -1 || map[x][y][z] == '#'){
continue;
}
steps[x][y][z] = steps[p.x][p.y][p.z] + 1;
if(end.x == x && end.y == y && end.z == z){
return steps[x][y][z];
}
q.add(new Pair(x,y,z));
}
}
return -1;
}
public static String nextLine()throws Exception {
return br.readLine();
}
static class Pair{
int x ;
int y ;
int z;
public Pair(int x, int y, int z){
this.x = x;
this.y = y;
this.z = z;
}
}
}
全球变暖
你有一张某海域 N×N像素的照片,”.”表示海洋、”#”表示陆地,如下所示:
.......
.##....
.##....
....##.
..####.
...###.
.......
其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿,例如上图就有 2座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。
具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
.......
.......
.......
.......
....#..
.......
.......
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
输入格式
第一行包含一个整数N。
以下 N 行 N 列,包含一个由字符”#”和”.”构成的 N×N 字符矩阵,代表一张海域照片,”#”表示陆地,”.”表示海洋。
照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。
输出格式
一个整数表示答案。
数据范围
1≤N≤1000
输入样例1:
7
.......
.##....
.##....
....##.
..####.
...###.
.......
输出样例1:
1
输入样例2:
9
.........
.##.##...
.#####...
.##.##...
.........
.##.#....
.#.###...
.#..#....
.........
输出样例2:
1
算法思路

题中的岛屿其实就是连通块,可以通过bfs来遍历每一个连通块中有多少个店即每一个岛屿中有多少个陆地块total,在bfs的过程中同时统计一个岛屿中有多少个陆地块是与海洋相邻的即bound,当total == bound说明此岛屿一定会被淹没,同时cnt加一,最后输出cnt就是所求答案。
flag 布尔类型数组来标记是否访问过某个单元格。
map字符数组用来存储整个地图
岛屿查找:
- 遍历每个位置 (i, j),如果当前位置是陆地 (map[i][j] == ‘#’) 且未被访问,则开始从此位置执行 BFS。
- 使用队列 q 进行 BFS,队列中保存待访问的陆地单元。
BFS过程:
- 初始化 total 和 bound,分别表示岛屿内陆地单元的数量和与海洋相邻的陆地单元数量。
- 对每个陆地单元,检查其四个相邻的方向(上下左右),如果相邻的位置是水域(map[x][y] == ‘.’),则标记为边界陆地;如果相邻的是未访问的陆地,继续将其加入队列。
- 如果岛屿的 total 数量等于 bound 数量,表示该岛屿会被淹没,返回 true,否则返回 false。
代码如下
import java.io.*;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 1010;
static int n;
static char[][] map = new char[N][N];
static boolean[][] flag = new boolean[N][N];
public static void main(String[] args) throws Exception{
n = Integer.parseInt(nextLine());
for(int i = 0; i < n; i++){
map[i] = nextLine().toCharArray();
}
//被淹没的岛屿的个数
int cnt = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(!flag[i][j] && map[i][j] == '#'){
if(bfs(i,j)){
cnt++;
}
}
}
}
pw.println(cnt);
pw.flush();
}
//total统计岛屿内的陆地单元个数
//bound统计岛屿内与海洋相邻的陆地个数
//如果 total == bound说明该岛屿会被淹没,反之不会被淹没
public static boolean bfs(int i, int j){
int total = 0;
int bound = 0;
Queue<Pair> q = new LinkedList<>();
q.add(new Pair(i,j));
flag[i][j] = true;
int[] dx = {1, -1, 0, 0};
int[] dy = {0, 0, 1, -1};
while(!q.isEmpty()){
Pair p = q.poll();
total++;
boolean is_bound = false;
for (int k = 0; k < 4; k++) {
int x = p.x + dx[k];
int y = p.y + dy[k];
if(x < 0 || x >= n || y < 0 || y >= n ){
//出界
continue;
}
if(flag[x][y]){
continue;
}
if(map[x][y] == '.'){
is_bound = true;
continue;
}
q.add(new Pair(x,y));
flag[x][y] = true;
}
if(is_bound){
bound++;
}
}
return bound == total;
}
public static String nextLine()throws Exception {
return br.readLine();
}
static class Pair{
int x;
int y;
Pair(){}
Pair(int x, int y){
this.x = x;
this.y = y;
}
}
}
大臣的旅费
很久以前,T 王国空前繁荣。
为了更好地管理国家,王国修建了大量的快速路,用于连接首都和王国内的各大城市。
为节省经费,T 国的大臣们经过思考,制定了一套优秀的修建方案,使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。
同时,如果不重复经过大城市,从首都到达每个大城市的方案都是唯一的。J 是 T 国重要大臣,他巡查于各大城市之间,体察民情。
所以,从一个城市马不停蹄地到另一个城市成了 J 最常做的事情。
他有一个钱袋,用于存放往来城市间的路费。聪明的 J 发现,如果不在某个城市停下来修整,在连续行进过程中,他所花的路费与他已走过的距离有关。
具体来说,一段连续的旅途里,第 1 千米的花费为 11,第 2
千米的花费为 12,第 3 千米的花费为 13,…,第 x 千米的花费为 x+10。
也就是说,如果一段旅途的总长度为 1 千米,则刚好需要花费 11,如果一段旅途的总长度为 2 千米,则第 1 千米花费 11,第 2 千米花费 12,一共需要花费 11+12=23。
J 大臣想知道:他从某一个城市出发,中间不休息,到达另一个城市,所有可能花费的路费中最多是多少呢?
输入格式
输入的第一行包含一个整数 n,表示包括首都在内的 T 王国的城市数。
城市从 1 开始依次编号,1 号城市为首都。
接下来 n−1 行,描述 T 国的高速路(T 国的高速路一定是 n−1 条)。
每行三个整数 Pi,Qi,Di,表示城市 Pi 和城市 Qi 之间有一条双向高速路,长度为 Di
千米。
输出格式
输出一个整数,表示大臣 J 最多花费的路费是多少。
数据范围
1≤n≤105,
1≤Pi,Qi≤n,
1≤Di≤1000
输入样例:
5
1 2 2
1 3 1
2 4 5
2 5 4
输出样例:
135
算法思路
输入解析:
- 输入树的节点数量 n。
- 通过 n-1 条边的输入构建树,树的边通过邻接表 u 存储,每条边记录两个节点 p 和 q 及其权重 w。
广度优先搜索 (BFS):
- 使用 BFS 查找从某个节点出发到其他所有节点的最短距离。
- BFS 初始化时,从任意节点(这里选择节点 1)开始搜索,遍历树的所有节点并记录其距离。
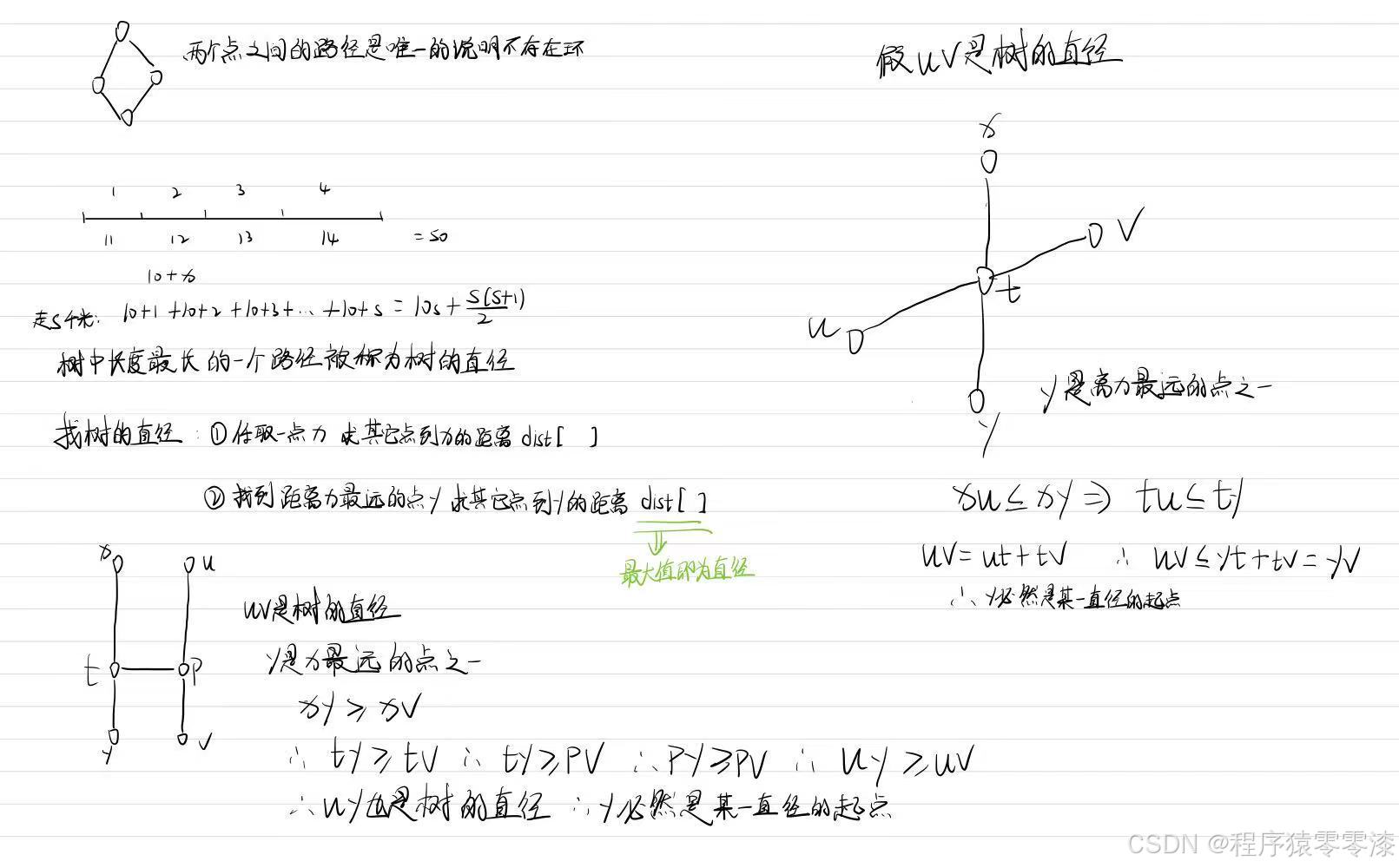
找到树的一个端点:
- 执行第一次 BFS 后,找到离节点 1 最远的节点 idx(这个节点是树的一个端点)。
计算树的直径:
- 使用找到的端点 idx 作为起点,执行第二次 BFS。计算从该端点出发的最远节点,并记录最大距离 maxv。这个最大距离即为树的直径。
结果计算:
- 根据树的直径 maxv,计算 (1 + maxv) * maxv / 2 + 10 * maxv,并输出结果。
代码如下
import java.util.*;
import java.lang.*;
import java.io.*;
public class Main {
static Scanner scanner = new Scanner(System.in);
static class Node {
public int v, w;
public Node(int v, int w) {
this.v = v;
this.w = w;
}
}
static int N = 100010;
static ArrayList<Node>[] u = new ArrayList[N];
static long[] dist = new long[N];
static void bfs(int idx) {
boolean[] vis = new boolean[N]; // 标记某节点是否搜过
Arrays.fill(dist, 0); // 初始化距离数组
ArrayDeque<Integer> ad = new ArrayDeque<>(); // 队列
ad.addLast(idx);
vis[idx] = true;
while (!ad.isEmpty()) {
int cur = ad.removeFirst();
for (Node e : u[cur]) { // 遍历邻接表
if (vis[e.v]) continue; // 如果已经遍历就跳过
dist[e.v] = dist[cur] + e.w; //更新下个节点的距离
ad.addLast(e.v); // 入队
vis[e.v] = true; // 标记为已搜过
}
}
}
public static void main(String[] args) {
int n = scanner.nextInt();
for (int i = 1; i < n; i++) {
int p = scanner.nextInt();
int q = scanner.nextInt();
int w = scanner.nextInt();
if (u[p] == null) u[p] = new ArrayList<>();
if (u[q] == null) u[q] = new ArrayList<>();
u[p].add(new Node(q, w));
u[q].add(new Node(p, w));
}
bfs(1);
int idx = 1;
long maxv = 0;
for (int i = 1; i <= n; i++) {
if (dist[i] > maxv) {
maxv = Math.max(maxv, dist[i]);
idx = i;
}
}
bfs(idx);
maxv = 0;
for (int i = 1; i <= n; i++) maxv = Math.max(maxv, dist[i]);
System.out.println((1 + maxv) * maxv / 2 + 10 * maxv);
}
}
总结
通过分析并解决《地牢大师》、《全球变暖》和《大臣的旅费》这三道算法题,我们不仅加深了对算法的理解,还掌握了如何灵活运用不同的算法思路与技巧。这些题目涵盖了广泛的知识点,包括图遍历、动态规划以及路径优化等,对我们提高编程能力和思维方式具有重要意义。在今后的编程实践中,掌握这些基本算法将帮助我们更高效地解决各类实际问题。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








