深度学习 实验二

 

一. 概念：张量、算子
          张量（tensor）理论是数学的一个分支学科，在力学中有重要应用。张量这一术语起源于力学，它最初是用来表示弹性介质中各点应力状态的，后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要，在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广，矢量是一阶张量。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。通俗来说，张量就是一个多重线性叠加数组。

          算子是一个函数空间到函数空间上的映射O：X→X。广义上的算子可以推广到任何空间，如内积空间等。

二. 使用pytorch实现张量运算
1.2 张量
1.2.1 创建张量
1.2.1.1 指定数据创建张量

通过给定Python列表数据，可以创建任意维度的张量。

（1）通过指定的Python列表数据[2.0, 3.0, 4.0]，创建一个一维张量。

import torch
a = [2,3,4]
b = torch.Tensor(a)
print(b)

输出

（2）通过指定的Python列表数据来创建类似矩阵（matrix）的二维张量。

import torch
X = torch.tensor([[1.0, 2.0, 3.0],
                 [4.0, 5.0, 6.0]])
print(X)

输出

 （3）同样地，还可以创建维度为3、4...N等更复杂的多维张量。

import torch
X = torch.tensor([[[1, 2, 3, 4, 5],
                   [6, 7, 8, 9, 10]],
                  [[11, 12, 13, 14, 15],
                   [16, 17, 18, 19, 20]]])
print(X)

输出

1.2.1.2 指定形状创建

      如果要创建一个指定形状、元素数据相同的张量，可以使用torch.zeros、torch.ones、torch.full等。

import torch
m, n = 2, 3
zeros_tensor = torch.zeros([m, n])
ones_tensor = torch.ones([m, n])
full_tensor = torch.full([m, n], 10)
print('zeros Tensor:\n', zeros_tensor)
print('ones Tensor:\n', ones_tensor)
print('full Tensor:\n', full_tensor)

输出

1.2.1.3 指定区间创建

            如果要在指定区间内创建张量，可以使用torch.arange、torch.linspace等。

import torch
arange_tensor = torch.arange(start=1, end=5, step=1)
linspace_tensor = torch.linspace(start=1, end=5, steps=5)
print('arange Tensor:\n', arange_tensor)
print('linspace Tensor:\n', linspace_tensor)

输出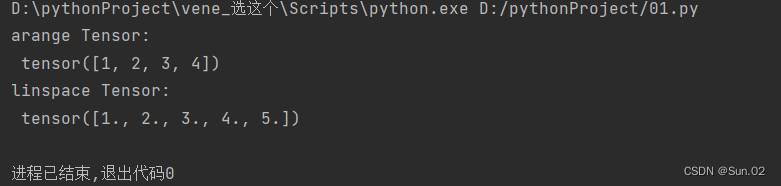

1.2.2 张量的属性
1.2.2.1 张量的形状

     张量具有如下形状属性：

• Tensor.ndim：张量的维度，例如向量的维度为1，矩阵的维度为2。
• Tensor.shape： 张量每个维度上元素的数量。
• Tensor.shape[n]：张量第n维的大小。第n维也称为轴。
• Tensor.numel()：张量中全部元素的个数。

import torch
X = torch.ones([2, 3, 4, 5])
print("Number of dimensions:", X.ndim)
print("Shape of Tensor:", X.shape)
print("Elements number along axis 0 of Tensor:", X.shape[0])
print("Elements number along the last axis of Tensor:", X.shape[-1])
print('Number of elements in Tensor: ', X.numel())

输出

1.2.2.2 形状的改变

            除了查看张