二叉树非递归遍历【使用堆栈】[有误]

最新推荐文章于 2025-05-15 04:22:49 发布

修花锦年喵

最新推荐文章于 2025-05-15 04:22:49 发布

阅读量611

点赞数

分类专栏：数据结构与算法文章标签：算法 c++ 开发语言

本文链接：https://blog.youkuaiyun.com/m0_62976227/article/details/122267496

版权

数据结构与算法专栏收录该内容

20 篇文章

订阅专栏

本文详细解析了二叉树的前序、中序和后序遍历算法，探讨了它们的本质和实现方式。针对每个遍历方法，作者提供了对应的代码实现，并指出在后序遍历中如何避免重复遍历，通过增加节点标记实现优化。此外，还给出了代码的修正版本，以确保正确性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前中后序其实本质上都是同一条路径，只不过是print的时候不同。

这条路径对于每一个根结点来说都会经过三次，第一次就print是前序，第二次print是中序，第三次print就是后序。

testcase：

124 5 67 38 9 【末尾三个空格。空格代表空树】

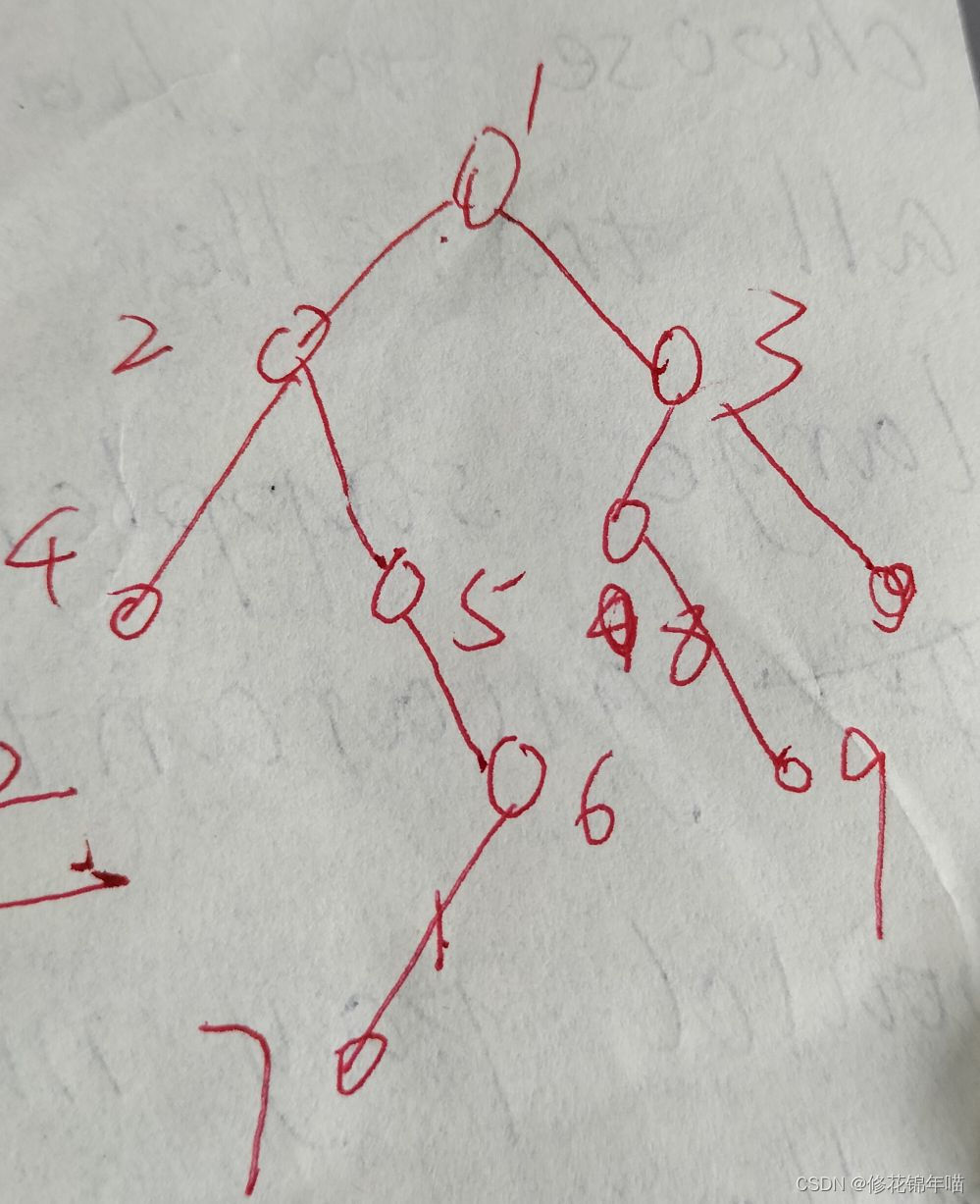
中序遍历的片段：

//中序遍历 
void TraversalTree(TreeNode* tree){
	Stack stack;
	stack.top=NULL;
	TreeNode*p=tree;
	int flag=0;
	while(p){
		//flag标记左子树有没有遍历过，1：遍历过 
		while(p->left&&(!flag)){
			//当p为有左子树的根时，把p推入栈中 
			Push(&stack,p);
			p=p->left;
			//TODO
		}
		//1.若经历了循环，此时p为最尾部的左子树，打印。
		//2.若未经历循环，此时p为 左子树遍历完全的父节点 
		printf("%d ",p->value);
		//如果p有右子树，则对右子树进行同样的操作 
		if(p->right!=NULL){
			flag=0;
			p=p->right;
			//TODO
		}
		else{
			//没有的话说明该节左子树遍历完全 
			flag=1;
			//如果栈为空，说明完成遍历 
			if(stack.lenth==0){
				p=NULL;
				//TODO
			}
			//否则将子树的父结点弹出，以遍历过的形态进行循环 
			else
				p=Pop(&stack);
		}
	}
}

同理前序遍历：

//前序遍历 
void TraversalTree(TreeNode* tree){
	Stack stack;
	stack.top=NULL;
	TreeNode*p=tree;
	int flag=0;
	while(p){ 
		if(!flag){
			while(p->left){
				Push(&stack,p);
				printf("%d ",p->value);
				p=p->left;
				//TODO
			}
			printf("%d ",p->value);
		}
		if(p->right!=NULL){
			flag=0;
			p=p->right;
			//TODO
		}
		else{
			flag=1;
			if(stack.lenth==0){
				p=NULL;
				//TODO
			}
			else
				p=Pop(&stack);
		}
	}
}

后序

//后序遍历  
void PostOrder(TreeNode* tree){
	Stack stack;
	stack.top=NULL;
	stack.lenth=0;
	TreeNode*p=tree;
	//左右树均被遍历 
	int flag=0;
	int flag2=0;
	while(p){ 
		if(!flag){
			if(!p->left&&p){
				Push(&stack,p);
				//TODO
			}
			if(p->left){
				while(p->left){
					Push(&stack,p);
					p=p->left;
				}
				if(p->right!=NULL){
					Push(&stack,p);
					p=p->right;
					flag=0;
					continue;
					//TODO
				}
				printf("%d ",p->value);
				p=(stack.top)->node;
				flag=1;
				continue;
				//TODO
			}	
		} 
		if(p->right!=NULL&&!flag2){
			flag=0;
			p=p->right;
			//TODO
		}
		else{
			flag=1;
			flag2=1;
			if(stack.lenth==0){
				p=NULL;
				//TODO
			}
			else{
				p=Pop(&stack);
				int c=p->value;
				printf("%d ",c);
				if(stack.lenth==1){
					if(c==(stack.top)->node->left->value){
						p=(stack.top)->node;
						flag2=0;//TODO
					}
					else{
						p=(stack.top)->node;
						printf("%d ",p->value);
						return;
					}
					//TODO
				}
			}
		}
	}
}

完整代码如下：

#include<stdlib.h>
#include <stdio.h>

typedef struct TreeNode{
	TreeNode*left;
	TreeNode*right;
	int value;
}TreeNode;

typedef struct Node{
	Node*bottom;
	TreeNode* node;
}Node;

typedef struct Stack{
	Node*top;
	int lenth;
}Stack;

TreeNode* CreateTreeNode(){
	TreeNode*p=(TreeNode*)malloc(sizeof(TreeNode));
	p->value=0;
	p->left=NULL;
	p->right=NULL;
	return p;
}

Node* CreateNode(){
	Node*p=(Node*)malloc(sizeof(Node));
	p->node=NULL;
	p->bottom=NULL;
	return p;
}

void Push(Stack *stack,TreeNode* tree){
	Node *p=CreateNode();
	p->node=tree;
	p->bottom=(*stack).top;
	(*stack).lenth++;
	(*stack).top=p;
}

TreeNode* Pop(Stack* stack){
	Node* p=(*stack).top;
	TreeNode* number=(*stack).top->node;
	(*stack).top=(*stack).top->bottom;
	(*stack).lenth--;
	return number;
}
//中序遍历 
void TraversalTree(TreeNode* tree){
	Stack stack;
	stack.top=NULL;
	TreeNode*p=tree;
	int flag=0;
	while(p){
		while(p->left&&!flag){
			Push(&stack,p);
			p=p->left;
			//TODO
		}
		printf("%d ",p->value);
		if(p->right!=NULL){
			flag=0;
			p=p->right;
			//TODO
		}
		else{
			flag=1;
			if(stack.lenth==0){
				p=NULL;
				//TODO
			}
			else
				p=Pop(&stack);
		}
	}
}

void CreateTree(TreeNode** root){
	char c;
	c=getchar();
	if(c==' '){
		*root=NULL;
		//TODO
	}
	else{
		*root=(TreeNode*)malloc(sizeof(TreeNode));
		if(*root==NULL){
			exit(1); 
			//TODO
		}
		(*root)->value=c-48;
		CreateTree(&((*root)->left));
		CreateTree(&((*root)->right));
	}
}

int main(){
	TreeNode* tree=(TreeNode*)malloc(sizeof(TreeNode));
	CreateTree(&tree);
	TraversalTree(tree);
	return 0; 
}

正确版本：

中序：

void InOrder(TreeNode* tree){
	Stack stack;
	stack.lenth=0;
	stack.top=NULL;
	TreeNode*p=tree;
	while(p||stack.lenth){
		while(p){
			Push(&stack,p);
			p=p->left;
			//TODO
		}
		if(stack.lenth){
			p=Pop(&stack);
			printf("%d ",p->value);
			p=p->right;
			//TODO
		}
	}
}

前序：（改为第一次遇到就print）

void PreOrder(TreeNode* tree){
	Stack stack;
	stack.lenth=0;
	stack.top=NULL;
	TreeNode*p=tree;
	while(p||stack.lenth){
		while(p){
			Push(&stack,p);
			printf("%d ",p->value);
			p=p->left;
			//TODO
		}
		if(stack.lenth){
			p=Pop(&stack);
			p=p->right;
			//TODO
		}
	}
}

前序和中序都是把根和左放在遍历完右树前输出。

而后序则是需要遍历完左右子树后才遍历根。所以为了防止多次遍历和胡乱pop，需要加一个tag来看是第几次经过根结点。如果是第二次经过结点，需要把它给push回去，并往它的右边遍历，同时将tag++；是第三次的话才能print出来，并且把p设置为空

这里设置为空思路很巧妙。

/*
define:

    typedef struct TreeNode{
	    TreeNode*left;
	    TreeNode*right;
    	int value;
	    int tag;
    }TreeNode;

*/

void PostOrder(TreeNode* tree){
	Stack stack;
	stack.lenth=0;
	stack.top=NULL;
	TreeNode*p=tree;
	while(p||stack.lenth){
		while(p){
			p->tag=1;
			Push(&stack,p);
			p=p->left;
			//TODO
		}
		if(stack.lenth){
			p=Pop(&stack);
			if(p->tag==1){
				p->tag++;
				Push(&stack,p);
				p=p->right; 
			}
			else if(p->tag==2){
				printf("%d ",p->value);
				p=NULL;
				//TODO
			}
		}
	}
}

如果删去p=NULL,而改成：

void PostOrder(TreeNode* tree){
	Stack stack;
	stack.lenth=0;
	stack.top=NULL;
	TreeNode*p=tree;
	while(1){
		while(p&&!p->tag){
			p->tag=1;
			Push(&stack,p);
			p=p->left;
			//TODO
		}
		if(stack.lenth){
			p=Pop(&stack);
			if(p->tag==1){
				p->tag++;
				Push(&stack,p);
				p=p->right; 
			}
			else if(p->tag==2){
				printf("%d ",p->value);
				if(!stack.lenth){
					break;
					//TODO
				}
				//TODO
			}
		}
	}
}

改变大while和小while循环条件，最后加了个终止条件。这也是可以的。

这说明了，设置为空的目的其实跟这个大抵是一样的，都是表明，这个根节点已经左右外加自己都完了，不用再来一遍了。原代码跟改后代码都使用了手段让其跳过左树遍历再pop一个出来。原来的代码使用p=NULL就可以安全退出循环，这个就达咩了。