目录
A. 多项式输出
说明
一元n次多项式可用如下的表达式表示:
其中,aixi称为i次项,ai称为i次项的系数。给出一个一元多项式各项的次数和系数,请按照如下规定的格式要求输出该多项式:
1. 多项式中自变量为x,从左到右按照次数递减顺序给出多项式。
2. 多项式中只包含系数不为0的项。
3. 如果多项式n次项系数为正,则多项式开头不出现“+”号,如果多项式n次项系数为负,则多项式以“-”号开头。
4. 对于不是最高次的项,以“+”号或者“-”号连接此项与前一项,分别表示此项系数为正或者系数为负。紧跟一个正整数,表示此项系数的绝对值(如果一个高于0次的项,其系数的绝对值为1,则无需输出1)。如果x 的指数大于1,则接下来紧跟的指数部分的形式为“x^b”,其中b为x的指数;如果x的指数为1,则接下来紧跟的指数部分形式为“x”;如果x的指数为0,则仅需输出系数即可。
5. 多项式中,多项式的开头、结尾不含多余的空格。
输入格式
每组输入数据共有2行。
第一行1个整数n,表示一元多项式的次数。
第二行有n+1个整数,其中第i个整数表示第n-i+1次项的系数,每两个整数之间用空格隔开。
数据规模:
1≤n≤ 100,多项式各次项系数的绝对值均不超过100。
输出格式
每组输出共1行,按题目所述格式输出多项式。
模拟就好了
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main() {
int n;
while (cin >> n) {
int x;
vector<string>v;
for (int i = 0; i <= n; i++) {
cin >> x;
string s;
if (i < n - 1) {//x后面一定要加系数时
if (x > 0) {
if (x > 1) {//x不等于1时要加上系数
s = to_string(x)+ "x^"+ to_string((n - i));
}
else {//x等于1时不需要
s = "x^"+to_string(n - i);
}
v.push_back(s);
}
if (x < 0) {
if (x < -1) {//x不等于-1时
s = to_string(x) + "x^" + to_string(n - i);
}
else s = "-x^" + to_string(n - i);//x等于-1时
v.push_back(s);
}
}
else if (i == n - 1) {//x的系数为1省略
if (x > 0) {
if (x > 1) {
s = to_string(x) + "x";
}
else s = "x";
v.push_back(s);
}
if (x < 0) {
if (x < -1) {
s = to_string(x) + "x";
}
else s = "-x";
v.push_back(s);
}
}
else if (i == n) {//没有x时
if (x > 0) {
s = to_string(x);
v.push_back(s);
}
if (x < 0) {
s = to_string(x);
v.push_back(s);
}
}
}
int t=v.size();
if(t==0){cout<<0;}//如果全为0,则输出0
else{//否则用加号连接
for (int i = 0; i < t; i++) {
cout << v[i];
if (i != (t - 1) && v[i + 1][0] != '-')cout << "+";
}
}
cout << endl;
}
return 0;
}B. 【基础】约瑟夫问题
说明
约瑟夫问题来源于公元1世纪的犹太历史学家Josephus。问题描述,有n个人(分别以编号1,2,3...n表示)围成一个圆圈,从编号为1的人开始进行1~m正向报数,报到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;如此重复下去,直到所有的人全部出列,求最后一个出列人的编号输入格式
输入文件仅有一行包含二个用空格隔开的整数N,M (2≤N≤100000,M≤10^9)。输出格式
输出文件仅有一行包含一个整数表示一个整数,表示最后一个人在队列中的编号。
我的暴力写法能过就没写推公式的了。思路就是每次找到要删除的位置删除该数据,最后剩下的一个即为答案
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main() {
int n, m, cnt = 0;
cin >> n >> m;
vector<int>v;
for (int i = 1; i <= n; i++)v.push_back(i);
while (v.size() > 1) {
cnt = (cnt + m - 1) % (v.size());
v.erase(v.begin() + cnt);
}
cout << v[0];
return 0;
}C. 计算系数
题目描述
给定一个多项式 (ax+by)^k ,请求出多项式展开后 x^n*y^m 项的系数。
输入格式
输入共一行,包含 5 个整数,分别为 a,b,k,n,m ,每两个整数之间用一个空格隔开。
输出格式
输出共 1 行,包含一个整数,表示所求的系数,这个系数可能很大,输出对 10007 取模后的结果。
对于其中某一项的系数,满足下方公式:

所以我们只需写出快速幂和组合数公式即可得出最终答案
对于组合数,满足下方公式:

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int mod = 10007;
ll a, b, k, n, m;
ll ksm(ll x, ll p) {
ll ans = 1 % mod;
while (p) {
if (p % 2 != 0)ans = (ans*x) % mod;
x = (x*x) % mod;
p /= 2;
}
return ans;
}
//Cn k=Cn (k-1) + C(n-1) (k-1);
int q[1005][1005];
ll C(int k, int n) {
q[k][n] %= mod;
if (q[k][n])return q[k][n];
else q[k][n] =(C(k-1, n)+ C(k - 1, n - 1))%mod;
return q[k][n];
}
int main() {
cin >> a >> b >> k >> n >> m;
a %= mod;
b %= mod;
for (int i = 0; i <= k; i++)q[i][0] = 1,q[i][i]=1;
ll x = ksm(a, n);
ll y = ksm(b, m);
x = (x * y) % mod;
ll p = C(k, min(n, m));
x = (x * p) % mod;
cout << x;
return 0;
}D. 海港
题目描述
小K是一个海港的海关工作人员,每天都有许多船只到达海港,船上通常有很多来自不同国家的乘客。
小K对这些到达海港的船只非常感兴趣,他按照时间记录下了到达海港的每一艘船只情况;对于第i艘到达的船,他记录了这艘船到达的时间 ��ti (单位:秒),船上的乘客数 ��ki,以及每名乘客的国籍 ��,1,��,2,…,��,�xi,1,xi,2,…,xi,k。
小K统计了 �n 艘船的信息,希望你帮忙计算出以每一艘船到达时间为止的 2424 小时( 2424 小时 =86400=86400 秒)内所有乘船到达的乘客来自多少个不同的国家。
形式化地讲,你需要计算 �n 条信息。对于输出的第 �i 条信息,你需要统计满足��−86400≤��≤��ti−86400≤tp≤ti 的船只 �p ,在所有的 ��,�xp,j 中,总共有多少个不同的数。
输入格式
第一行输入一个正整数�n,表示小K统计了�n艘船的信息。
接下来 �n 行,每行描述一艘船的信息:前两个整数 ��ti 和 ��ki 分别表示这艘船到达海港的时间和船上的乘客数量,接下来 ��ki 个整数 ��,�xi,j 表示船上乘客的国籍。
保证输入的 ��ti 是递增的,单位是秒;表示从小K第一次上班开始计时,这艘船在第 ��ti 秒到达海港。
保证 1≤�≤1051≤n≤105,∑��≤3×105∑ki≤3×105 ,1≤��,�≤1051≤xi,j≤105, 1≤��−1≤��≤1091≤ti−1≤ti≤109。
其中∑��∑ki表示所有的��ki的和。
输出格式
输出 �n 行,第 �i 行输出一个整数表示第 �i 艘船到达后的统计信息。
输入数据 1
3 1 4 4 1 2 2 2 2 2 3 10 1 3Copy
输出数据 1
3 4 4Copy
样例 1 说明
第一艘船在第 11 秒到达海港,最近2424小时到达的船是第一艘船,共有 44 个乘客, 分别是来自国家 4,1,2,24,1,2,2,共来自 33 个不同的国家;
第二艘船在第 22 秒到达海港,最近 2424小时到达的船是第一艘船和第二艘船,共有 4+2=64+2=6 个乘客,分别是来自国家 4,1,2,2,2,34,1,2,2,2,3,共来自 44 个不同的国家;
第三艘船在第 1010 秒到达海港,最近 2424 小时到达的船是第一艘船、第二艘船和第 三艘船,共有 4+2+1=74+2+1=7 个乘客,分别是来自国家 4,1,2,2,2,3,34,1,2,2,2,3,3 ,共来自44个不同 的国家。
输入数据 2
4 1 4 1 2 2 3 3 2 2 3 86401 2 3 4 86402 1 5Copy
输出数据 2
3 3 3 4Copy
样例 2 说明
第一艘船在第 11 秒到达海港,最近 2424 小时到达的船是第一艘船,共有 44 个乘客,分别是来自国家 1,2,2,31,2,2,3 ,共来自 33 个不同的国家。
第二艘船在第 33 秒到达海港,最近 2424 小时到达的船是第一艘船和第二艘船,共有 4+2=64+2=6 个乘客,分别是来自国家 1,2,2,3,2,31,2,2,3,2,3,共来自 33 个不同的国家。
第三艘船在第 8640186401 秒到达海港,最近 2424 小时到达的船是第二艘船和第三艘船,共有 2+2=42+2=4 个乘客,分别是来自国家 2,3,3,42,3,3,4,共来自 33 个不同的国家。
第四艘船在第 8640286402 秒到达海港,最近 2424 小时到达的船是第二艘船、第三艘船和第四艘船,共有 2+2+1=52+2+1=5 个乘客,分别是来自国家 2,3,3,4,52,3,3,4,5,共来自 44 个不同的国家。
数据范围与提示
对于 10%10%的测试点,�=1,∑��≤10,1≤��,�≤10,1≤��≤10n=1,∑ki≤10,1≤xi,j≤10,1≤ti≤10;
对于 20%20%的测试点,1≤�≤10,∑��≤100,1≤��,�≤100,1≤��≤327671≤n≤10,∑ki≤100,1≤xi,j≤100,1≤ti≤32767;
对于 40%40%的测试点,1≤�≤100,∑��≤100,1≤��,�≤100,1≤��≤864001≤n≤100,∑ki≤100,1≤xi,j≤100,1≤ti≤86400;
对于 70%70%的测试点,1≤�≤1000,∑��≤3000,1≤��,�≤1000,1≤��≤1091≤n≤1000,∑ki≤3000,1≤xi,j≤1000,1≤ti≤109;
对于 100%100%的测试点,1≤�≤105,∑��≤3×105,1≤��,�≤105,1≤��≤1091≤n≤105,∑ki≤3×105,1≤xi,j≤105,1≤ti≤109。
用ans来记录到当前的答案数,用结构体存国籍和时间,每次输入前判断队列是否为空或者当前的时间是否与队列中的元素超过24小时,每次更新队列和答案得出结果
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n;
int ans;//记录答案
struct app{
int t,x;//t表示时间,x表示国籍
};
queue<app>q;
map<int,int>m;//国籍对应的人数
int main(){
cin>>n;
for(int i=0;i<n;i++){
int t,k;
cin>>t>>k;
while(q.front().t+86400<=t&&q.size()){
m[q.front().x]--;
if(m[q.front().x]==0){//人数归0则答案减1
ans--;
}
q.pop();
}
for(int i=0;i<k;i++){
int p;
cin>>p;
m[p]++;
if(m[p]==1)ans++;//新国籍答案+1
q.push({t,p});
}
cout<<ans<<"\n";
}
return 0;
}E. 机器翻译
题目描述
小晨的电脑上安装了一个机器翻译软件,他经常用这个软件来翻译英语文章。
这个翻译软件的原理很简单,它只是从头到尾,依次将每个英文单词用对应的中文含义来替换。对于每个英文单词,软件会先在内存中查找这个单词的中文含义,如果内存中有,软件就会用它进行翻译;如果内存中没有,软件就会在外存中的词典内查找,查出单词的中文含义然后翻译,并将这个单词和译义放入内存,以备后续的查找和翻译。
假设内存中有 �m 个单元,每单元能存放一个单词和译义。每当软件将一个新单词存入内存前,如果当前内存中已存入的单词数不超过 �−1m−1,软件会将新单词存入一个未使用的内存单元;若内存中已存入 �m 个单词,软件会清空最早进入内存的那个单词,腾出单元来,存放新单词。
假设一篇英语文章的长度为 �n 个单词。给定这篇待译文章,翻译软件需要去外存查找多少次词典?假设在翻译开始前,内存中没有任何单词。
输入格式
输入共 22 行。每行中两个数之间用一个空格隔开。
第一行为两个正整数 �m 和 �n,代表内存容量和文章的长度。
第二行为 �n 个非负整数,按照文章的顺序,每个数(大小不超过 10001000)代表一个英文单词。文章中两个单词是同一个单词,当且仅当它们对应的非负整数相同。输出格式
输出共 11 行,包含一个整数,为软件需要查词典的次数。
输入数据 1
3 7 1 2 1 5 4 4 1Copy
输出数据 1
5Copy
样例 1 说明
整个查字典过程如下:每行表示一个单词的翻译,冒号前为本次翻译后的内存状况:
空:内存初始状态为空。
- 11:查找单词 11 并调入内存;
- 11 22:查找单词 22 并调入内存;
- 11 22:在内存中找到单词 11 ;
- 11 22 55:查找单词 55 并调入内存;
- 22 55 44:查找单词 44 并调入内存替代单词 11;
- 22 55 44:在内存中找到单词 44 ;
- 55 44 11:查找单词 11 并调入内存替代单词 22。
共计查了 55 次词典。
输入数据 2
2 10 8 824 11 78 11 78 11 78 8 264Copy
输出数据 2
6Copy
数据范围与提示
对于 10%10% 的数据有 �=1m=1,�≤5n≤5;
对于 100%100% 的数据有 0<�≤1000<m≤100,0<�≤10000<n≤1000。
队列题,限定队的长度,如果出现了超出长度的则队首元素出队,答案加1;否则直接入队答案+1,注意:这里的队内元素是不重复的,重复的不入队
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt;
int main(){
cin>>m>>n;
queue<int>a;
map<int,int>mm;
for(int i=0;i<n;i++){
int x;
cin>>x;
mm[x]++;
if(mm[x]==1){
if(a.size()<m){
a.push(x);
cnt++;
}
else{
mm[a.front()]=0;
a.pop();
cnt++;
a.push(x);
}
}
}
cout<<cnt;
return 0;
}F.佩奇玩游戏
一条马路上趴着很多青蛙,佩奇正好非常无聊,打算逗弄一下这些青蛙作为打发时间的游戏。她站在笔直的马路上,她的前方趴着 N 只青蛙(可以看作一条直线上有N只青蛙),这些青蛙的编号从近到远依次为 1,2,⋯,N 。每只青蛙的初始位置与佩奇的距离是已知的,从近到远分别为 �1A1,�2A2,...��An 。可能有多只青蛙与佩奇的距离相同。佩奇从最初的位置一直向前走,经过奇数只青蛙的时候会逗弄一下这只青蛙,这只青蛙受到惊吓会向前跳 D 米,路过偶数只青蛙的时候什么也不做(没有被逗弄的青蛙不会移动)。重复这个过程直到佩奇前方没有青蛙,到此游戏结束。
需要注意一只青蛙向前跳跃后,佩奇继续往前走还会遇到它,由于佩奇记不清前面是否已遇到过这只青蛙,这只青蛙会被当成尚未遇见的并重复计数,因此一只青蛙可能会被逗弄多次。当佩奇经过的一个位置同时趴着多只青蛙时,佩奇会将这些青蛙按照初始编号排序,初始编号小的看做离自己更近。
现在佩奇想要知道游戏结束时,离佩奇初始位置最远的青蛙与佩奇初始位置的距离是多少。
Format
Input
输入共两行。
第一行包含 2 个由空格分隔的正整数,分别表示青蛙的数量 N(1≤N≤105105) 和青蛙受到惊吓后跳跃的距离 D(1≤D≤109109)。第二行包含 N 个由空格分隔的正整数,从左到右分别为�1A1,�2A2,...��AN (1≤�1A1,≤�2A2,≤⋯≤��AN≤109109,),分别表示 N 只青蛙的初始位置与佩奇初始位置的距离。 .
Output
输出是一个整数,表示游戏结束时,离佩奇初始位置最远的青蛙与佩奇初始位置的距离。
娱乐:关于oj的好玩的东西:栈清空了还能输出栈顶元素(ps:别这样搞编译器过不去)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int cnt;
priority_queue<ll,vector<ll>,greater<ll> >q;
int main(){
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++){
int x;
cin>>x;
q.push(x);
}
while(q.size()){
cnt++;
if(cnt%2!=0){
ll t=q.top();
t+=m;
q.push(t);
}
q.pop();
}
cout<<q.top();
return 0;
}正解: 拿一个东西记录最大值
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int cnt;
priority_queue<ll,vector<ll>,greater<ll> >q;
//这玩意叫优先队列
//加了greater<ll>表示从小到大
int main(){
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++){
int x;
cin>>x;
q.push(x);
}
ll ans=0;
while(q.size()){
cnt++;
ans=max(ans,q.top());
if(cnt%2!=0){
ll t=q.top();
t+=m;
q.push(t);
}
q.pop();
}
cout<<ans;
return 0;
}







 文章提供了若干编程问题的解决方案,包括多项式输出的格式化,约瑟夫问题的暴力求解,计算多项式展开的特定项系数,处理海港乘客国籍统计,机器翻译的单词查找算法,以及佩奇游戏中的青蛙跳跃距离计算。这些问题涉及数据结构、算法和数学知识。
文章提供了若干编程问题的解决方案,包括多项式输出的格式化,约瑟夫问题的暴力求解,计算多项式展开的特定项系数,处理海港乘客国籍统计,机器翻译的单词查找算法,以及佩奇游戏中的青蛙跳跃距离计算。这些问题涉及数据结构、算法和数学知识。
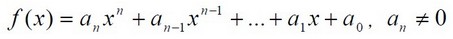

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








