【】(最小生成树，剪枝）

 题目

思考

我们应该选择哪一个最小生成树算法呢？

并查集的kruskal和堆优化的prim

时间复杂度分别为：和

一般情况下都使用 Kruskal 算法，在稠密图尤其是完全图上，暴力 Prim 的复杂度比 Kruskal 优，但 不一定 实际跑得更快。

在这里面临一个完全图问题，显然超过了1e8，所以我们需要把图上存在的边进行剪枝，如何剪枝呢？

结论：存在一颗最小生成树，它的每个权值都小于等于n，只需要保存小于等于n的边

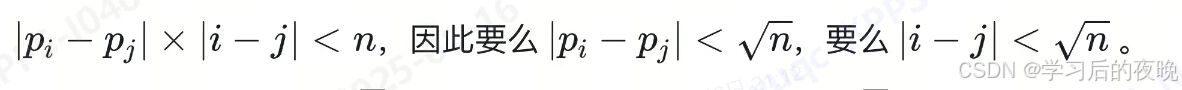
有了这个结论后，暴力枚举所有情况i和j的情况ÿ